Відмінності між версіями «Часові характеристики»
Halinka (обговорення • внесок) |
Halinka (обговорення • внесок) |
||
| (Не показано 5 проміжних версій цього користувача) | |||
| Рядок 3: | Рядок 3: | ||
Часова характеристика ланки при законі зміни одиничної сходинкової дії називається перехідною характеристикою, а при законі зміни дельта-функції – імпульсно-перехідною характеристико.Кожна з них є вичерпною характеристикою системи та будь-якої її ланки за нульових початкових умов. За ними можна точно визначити вихідну величину під час довільного вхідного впливу. | Часова характеристика ланки при законі зміни одиничної сходинкової дії називається перехідною характеристикою, а при законі зміни дельта-функції – імпульсно-перехідною характеристико.Кожна з них є вичерпною характеристикою системи та будь-якої її ланки за нульових початкових умов. За ними можна точно визначити вихідну величину під час довільного вхідного впливу. | ||
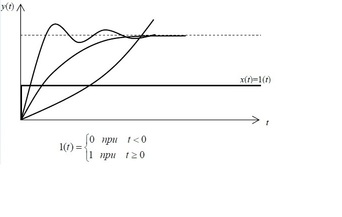
:''' Перехідною характеристикою '''називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одинична сходинкова дія. Аналітичним виразом для перехідної характеристики є перехідна функція, яка позначається h(t). Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при впливі одиничної сходинкової дії при нульових початкових умовах. | :''' Перехідною характеристикою '''називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одинична сходинкова дія. Аналітичним виразом для перехідної характеристики є перехідна функція, яка позначається h(t). Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при впливі одиничної сходинкової дії при нульових початкових умовах. | ||
| − | [[Файл:1перехідна_характер1.jpg]] | + | [[Файл:1перехідна_характер1.jpg|347px|thumb|right|Перехідні характеристики]] |
| + | |||
Перехідна функція відбиває реакцію елементу або системи в цілому на одиничну сходинку дію при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході. '''Одинична сходинкова дія''' – це дія, яка миттєво змінюється від нуля до одиниці і надалі залишається незмінною. Аналітичним виразом одиничної сходинкової дії є одинична сходинкова функція, яка позначається 1(t). Перехідна функція може бути отримана шляхом рішення диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом. | Перехідна функція відбиває реакцію елементу або системи в цілому на одиничну сходинку дію при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході. '''Одинична сходинкова дія''' – це дія, яка миттєво змінюється від нуля до одиниці і надалі залишається незмінною. Аналітичним виразом одиничної сходинкової дії є одинична сходинкова функція, яка позначається 1(t). Перехідна функція може бути отримана шляхом рішення диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом. | ||
:'''Імпульсно перехідною характеристикою''' називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одиничний імпульс. | :'''Імпульсно перехідною характеристикою''' називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одиничний імпульс. | ||
:'''Одиничний імпульс''' – це імпульс, площа якого дорівнює одиниці при тривалості, що дорівнює нулю і висоті, рівній нескінченості. Одиничний імпульс – це математична ідеалізація гранично короткого імпульсного сигналу. | :'''Одиничний імпульс''' – це імпульс, площа якого дорівнює одиниці при тривалості, що дорівнює нулю і висоті, рівній нескінченості. Одиничний імпульс – це математична ідеалізація гранично короткого імпульсного сигналу. | ||
Аналітичним виразом для імпульсної перехідної характеристики є імпульсна перехідна функція або вагова функція (функція ваги), яка позначається ω(t). Вираз для одиничного імпульсу називається одиничною імпульсною функцією або дельта-функцією і позначається δ(t). Таким чином ω(t) – це y(t) при x(t)= δ(t). Дельта-функція просто зв’язана з одиничною сходинковою дією: дельта-функція є похідною від одинчиної сходинкової дії. | Аналітичним виразом для імпульсної перехідної характеристики є імпульсна перехідна функція або вагова функція (функція ваги), яка позначається ω(t). Вираз для одиничного імпульсу називається одиничною імпульсною функцією або дельта-функцією і позначається δ(t). Таким чином ω(t) – це y(t) при x(t)= δ(t). Дельта-функція просто зв’язана з одиничною сходинковою дією: дельта-функція є похідною від одинчиної сходинкової дії. | ||
Поточна версія на 21:07, 8 травня 2011
- Часовою характеристикою ланки називається графік зміни вихiдної величини y(t) по визначеному закону i при умовi, що до прикладення зовнiшньої дiї ланка була в станi спокою.
Часові характеристики залежать від властивостей системи i вiд характеру зовнішньої дiї, для якої вони визначаються. Можна розглядати цi характеристики по вхiднiй дії x і по збуренню f . При визначеннi часових характеристик по якiй-небудь зовнiшнiй дiї інші дії дорiвнюють нулю.Найчастіше розглядають часові характеристики , які змінюються по закону одиничної сходинкової дії, або по закону дельта-функції. Часова характеристика ланки при законі зміни одиничної сходинкової дії називається перехідною характеристикою, а при законі зміни дельта-функції – імпульсно-перехідною характеристико.Кожна з них є вичерпною характеристикою системи та будь-якої її ланки за нульових початкових умов. За ними можна точно визначити вихідну величину під час довільного вхідного впливу.
- Перехідною характеристикою називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одинична сходинкова дія. Аналітичним виразом для перехідної характеристики є перехідна функція, яка позначається h(t). Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при впливі одиничної сходинкової дії при нульових початкових умовах.
Перехідна функція відбиває реакцію елементу або системи в цілому на одиничну сходинку дію при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході. Одинична сходинкова дія – це дія, яка миттєво змінюється від нуля до одиниці і надалі залишається незмінною. Аналітичним виразом одиничної сходинкової дії є одинична сходинкова функція, яка позначається 1(t). Перехідна функція може бути отримана шляхом рішення диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом.
- Імпульсно перехідною характеристикою називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одиничний імпульс.
- Одиничний імпульс – це імпульс, площа якого дорівнює одиниці при тривалості, що дорівнює нулю і висоті, рівній нескінченості. Одиничний імпульс – це математична ідеалізація гранично короткого імпульсного сигналу.
Аналітичним виразом для імпульсної перехідної характеристики є імпульсна перехідна функція або вагова функція (функція ваги), яка позначається ω(t). Вираз для одиничного імпульсу називається одиничною імпульсною функцією або дельта-функцією і позначається δ(t). Таким чином ω(t) – це y(t) при x(t)= δ(t). Дельта-функція просто зв’язана з одиничною сходинковою дією: дельта-функція є похідною від одинчиної сходинкової дії.