Відмінності між версіями «Формула Торрічеллі»
Eskimos (обговорення • внесок) |
|||
| (Не показані 59 проміжних версій ще одного користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | :[[Зображення:Clip_image102.gif]] Застосуємо рівняння | + | == Біографія == |
| − | :[[Зображення: | + | [[Зображення:Torricelli.jpg|right|thumb]] |
| + | |||
| + | Італійський математик і фізик '''Эванджелиста Торрічеллі''' народився у Фаэнце в небагатій сім'ї; виховувався у дядька, бенедиктинского ченця. Вчився в ієзуїтському коледжі, а потім отримав математичну освіту в Римі у б. Кастелли, друга і учня Г. Галілея. У 1641 р. Торрічеллі переїхав в Арчетри, де допомагав Галілею в обробці його праць. З 1642 р., після смерті Галілея, придворний математик великого герцога Тосканського і одночасно професор математики Флорентійського університету. | ||
| + | |||
| + | Найбільш відомі праці Торрічеллі в області пневматики і механіки. У 1643 р. він показав, що повітря має вагу і що насос не може витягнути воду на висоту більше 10 м. У 1644 р. розвинув теорію атмосферного тиску довів можливість отримання так званої "торічелієвої порожнечі" (тим самим завдавши удару за арістотелівським твердженням "природа боїться порожнечі") і винайшов ртутний барометр. Виявив зміну висоти ртутного стовпа залежно від погодних умов пояснив вітер змінами атмосферного тиску. Відкриття і дослідження атмосферного тиску викликало великий резонанс серед учених-сучасників. | ||
| + | |||
| + | У своїй основній праці по механіці "Про рух тих, що вільно падають і кинутих важких тіл" (1641) Торрічеллі розвивав ідеї Галілея про рух, сформулював принцип руху центрів тяжіння, встановив параболічність траєкторії тіл, кинутих під кутом до горизонту довів інші теореми балістики. Торрічеллі заклав основи гідравліки, вивів формулу для швидкості витікання ідеальної рідини з посудини (формула Торрічеллі). Йому належать також роботи по математиці (зокрема, розвинув метод "недільних") і балістиці удосконаленню оптичних приладів, шліфовці лінз. Удосконалив повітряний термоскоп Галілея, переробивши його в спиртовий термометр. | ||
| + | |||
| + | == Доведення == | ||
| + | Скористаємось рівнянням Бернуллі, записаним у вигляді: | ||
| + | :[[Зображення:74b39eda5b06625cf72598e69f4c6c20.png]] | ||
| + | |||
| + | де: V — швидкість руху рідини; | ||
| + | :z — висота підняття рідини у розглядуваній точці відносно площини відліку (площини порівняння); | ||
| + | :p — тиск у розглядуваній точці; | ||
| + | :ρ — густина (питома маса) рідини. | ||
| + | |||
| + | Приймемо, що отвір знаходиться на висоті z = 0. У верхній частині бака, тиск p дорівнює атмосферному тиску і швидкістьV можна вважати нульовою, так як швидкість опускання рівня у баку значно менша, ніж швидкість витікання рідини з бака. На отворі, z=0 і тиск p знову ж таки рівний атмосферному. Тоді рівняння Бернуллі для двох перерізів: на поверхні рідини у баку і перерізу отвору з врахуванням зроблених вище допущень, запишуться: | ||
| + | :[[Зображення:5809fa1578e84623ac86f28a5e6cad28.png]] | ||
| + | :[[Зображення:02d4191b01f4d68c94dd06c3267431cc.png]] | ||
| + | :[[Зображення:536e2a05ad96193343b5f94520935a67.png]] | ||
| + | |||
| + | z відповідає h, обумовленому на початку, тому: | ||
| + | :[[Зображення:8996d6e842a53b7eccae14493f997f99.png]] | ||
| + | |||
| + | [[Зображення:Clip_image102.gif|left|thumb|мал. 1]] | ||
| + | |||
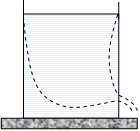
| + | Застосуємо рівняння Бернуллі до витікання рідини з невеликого отвору в широкій посудині. Виділимо трубку струму (мал. 1). У кожному перерізі швидкість і висоту над деяким початковим рівнем можна вважати постійною. Тиск в обох перерізах дорівнює атмосферному. Швидкість переміщення відкритої поверхні багато менше швидкості витікання рідини з отвору, тому можна вважати її рівною нулю. Ця формула називається формулою Торрічеллі і визначає швидкість витікання рідини з отвору. Вона отримана для ідеальної рідини. | ||
| + | <center>[[Зображення:Clip_image106.gif]]</center> | ||
| + | |||
| + | Тоді звідси [[Зображення:Clip_image108.gif]], де [[Зображення:Clip_image110.gif]]. Ця формула називається формулою Торрічеллі і визначає швидкість витікання рідини з отвору. Вона отримана для ідеальної рідини. | ||
| + | |||
| + | З формули Торрічеллі виходить, що швидкість витікання рідини з отвору однакова для усіх рідин і залежить лише від висоти, з якою рідина опустилася. Вона виявляється рівній швидкості вільного падіння тіла з тієї ж висоти. Для реальних рідин швидкість буде менше, вона залежить від форми, розміру отвору і від в'язкості рідини. | ||
| + | |||
| + | == Формула Торрічеллі для в'язкої рідини == | ||
| + | |||
| + | Дійсна ж швидкість витікання дещо відрізняється від швидкості, яка визначається формулою Торрічеллі: вона залежить від форми і розміру отвору, від в'язкості рідини та величини витрати. Для врахування цих обставин у формулу Торрічеллі вводять поправочний множник, що завжди менший від одиниці. Тоді формула набуває вигляду: | ||
| + | |||
| + | :[[Зображення:9a7605ac16c2d5c5ba9c4f664bc13569.png]] | ||
| + | |||
| + | де φ — коефіцієнт швидкості при витіканні рідини з отвору. | ||
| + | |||
| + | Для малого круглого отвору при великих числах Рейнольдса він дорівнює [[Зображення:8821d3d8fb19767f249f34b76c0301c4.png]] Значення φ для отворів інших форм і розмірів наводяться в довідниках з гідравліки. | ||
| + | |||
| + | == Джерела == | ||
| + | http://ido.tsu.ru/schools/physmat/data/res/mehanika/uchpos/text/6_4.html | ||
| + | |||
| + | http://ido.tsu.ru/schools/physmat/data/res/mehanika/uchpos/ | ||
| + | |||
| + | http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Torricelli.html | ||
| + | |||
| + | http://uk.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%A2%D0%BE%D1%80%D1%80%D1%96%D1%87%D0%B5%D0%BB%D0%BB%D1%96 | ||
Поточна версія на 20:40, 12 травня 2011
Біографія
Італійський математик і фізик Эванджелиста Торрічеллі народився у Фаэнце в небагатій сім'ї; виховувався у дядька, бенедиктинского ченця. Вчився в ієзуїтському коледжі, а потім отримав математичну освіту в Римі у б. Кастелли, друга і учня Г. Галілея. У 1641 р. Торрічеллі переїхав в Арчетри, де допомагав Галілею в обробці його праць. З 1642 р., після смерті Галілея, придворний математик великого герцога Тосканського і одночасно професор математики Флорентійського університету.
Найбільш відомі праці Торрічеллі в області пневматики і механіки. У 1643 р. він показав, що повітря має вагу і що насос не може витягнути воду на висоту більше 10 м. У 1644 р. розвинув теорію атмосферного тиску довів можливість отримання так званої "торічелієвої порожнечі" (тим самим завдавши удару за арістотелівським твердженням "природа боїться порожнечі") і винайшов ртутний барометр. Виявив зміну висоти ртутного стовпа залежно від погодних умов пояснив вітер змінами атмосферного тиску. Відкриття і дослідження атмосферного тиску викликало великий резонанс серед учених-сучасників.
У своїй основній праці по механіці "Про рух тих, що вільно падають і кинутих важких тіл" (1641) Торрічеллі розвивав ідеї Галілея про рух, сформулював принцип руху центрів тяжіння, встановив параболічність траєкторії тіл, кинутих під кутом до горизонту довів інші теореми балістики. Торрічеллі заклав основи гідравліки, вивів формулу для швидкості витікання ідеальної рідини з посудини (формула Торрічеллі). Йому належать також роботи по математиці (зокрема, розвинув метод "недільних") і балістиці удосконаленню оптичних приладів, шліфовці лінз. Удосконалив повітряний термоскоп Галілея, переробивши його в спиртовий термометр.
Доведення
Скористаємось рівнянням Бернуллі, записаним у вигляді:
де: V — швидкість руху рідини;
- z — висота підняття рідини у розглядуваній точці відносно площини відліку (площини порівняння);
- p — тиск у розглядуваній точці;
- ρ — густина (питома маса) рідини.
Приймемо, що отвір знаходиться на висоті z = 0. У верхній частині бака, тиск p дорівнює атмосферному тиску і швидкістьV можна вважати нульовою, так як швидкість опускання рівня у баку значно менша, ніж швидкість витікання рідини з бака. На отворі, z=0 і тиск p знову ж таки рівний атмосферному. Тоді рівняння Бернуллі для двох перерізів: на поверхні рідини у баку і перерізу отвору з врахуванням зроблених вище допущень, запишуться:
z відповідає h, обумовленому на початку, тому:
Застосуємо рівняння Бернуллі до витікання рідини з невеликого отвору в широкій посудині. Виділимо трубку струму (мал. 1). У кожному перерізі швидкість і висоту над деяким початковим рівнем можна вважати постійною. Тиск в обох перерізах дорівнює атмосферному. Швидкість переміщення відкритої поверхні багато менше швидкості витікання рідини з отвору, тому можна вважати її рівною нулю. Ця формула називається формулою Торрічеллі і визначає швидкість витікання рідини з отвору. Вона отримана для ідеальної рідини.
Тоді звідси ![]() , де
, де ![]() . Ця формула називається формулою Торрічеллі і визначає швидкість витікання рідини з отвору. Вона отримана для ідеальної рідини.
. Ця формула називається формулою Торрічеллі і визначає швидкість витікання рідини з отвору. Вона отримана для ідеальної рідини.
З формули Торрічеллі виходить, що швидкість витікання рідини з отвору однакова для усіх рідин і залежить лише від висоти, з якою рідина опустилася. Вона виявляється рівній швидкості вільного падіння тіла з тієї ж висоти. Для реальних рідин швидкість буде менше, вона залежить від форми, розміру отвору і від в'язкості рідини.
Формула Торрічеллі для в'язкої рідини
Дійсна ж швидкість витікання дещо відрізняється від швидкості, яка визначається формулою Торрічеллі: вона залежить від форми і розміру отвору, від в'язкості рідини та величини витрати. Для врахування цих обставин у формулу Торрічеллі вводять поправочний множник, що завжди менший від одиниці. Тоді формула набуває вигляду:
де φ — коефіцієнт швидкості при витіканні рідини з отвору.
Для малого круглого отвору при великих числах Рейнольдса він дорівнює ![]() Значення φ для отворів інших форм і розмірів наводяться в довідниках з гідравліки.
Значення φ для отворів інших форм і розмірів наводяться в довідниках з гідравліки.
Джерела
http://ido.tsu.ru/schools/physmat/data/res/mehanika/uchpos/text/6_4.html
http://ido.tsu.ru/schools/physmat/data/res/mehanika/uchpos/
http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Torricelli.html