Відмінності між версіями «Повний факторний експеримент»
(Створена сторінка: Повний факторний експеримент (ПФЕ) – експеримент, що реалізує всі можливі неповторювані …) |
(Cleaning up links to custom-essay-writing-service.org) |
||
| (Не показані 11 проміжних версій 2 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | Повний факторний експеримент (ПФЕ) – експеримент, що реалізує всі можливі неповторювані комбінації незалежних змінних, кожна з яких примусово (активно) варіює на двох рівнях. Число цих комбінацій при n факторах N = 2^n і визначає тип планування. | + | {{Завдання|Гуменюу І.|Назаревич О. Б.| 20 березня 2011}} |
| + | |||
| + | {{Студент |img=Нема | Name=Гуменюк| Surname= Ірина| FatherNAme= |Faculti=ФІС | Group=СНм-51 | Zalbook=СН-10-078}} | ||
| + | Повний факторний експеримент (ПФЕ) – експеримент, що реалізує всі можливі неповторювані комбінації незалежних змінних, кожна з яких примусово (активно) варіює на двох рівнях. Число цих комбінацій при n факторах <math>N = 2^n</math> і визначає тип планування. | ||
| + | ==Основні відомості == | ||
| + | |||
| + | ПФЕ дає можливість знайти роздільні оцінки коефіцієнтів bі. Оскільки використовується поліном першого порядку, то план такого експерименту називають планом першого порядку. | ||
| + | *Знаходження моделі методом ПФЕ складається з: | ||
| + | *планування експерименту; | ||
| + | *власне експерименту; | ||
| + | *перевірки відтворюваності (однорідності вибіркових дисперсій); | ||
| + | *утворення математичної моделі об’єкта з перевіркою статистичної значущості вибіркових коефіцієнтів регресії; | ||
| + | *перевірки адекватності математичного опису. | ||
| + | |||
| + | ==Двофакторний експеримент== | ||
| + | |||
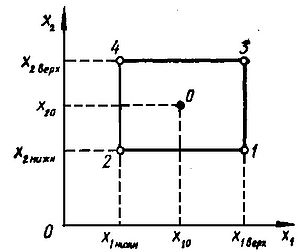
| + | Для двофакторної задачі область факторного простору, що підлягає вивченню, має вигляд прямокутника (рисунок 2) з координатами кутових точок: 1 – (х1, х2); 2 – (х1, х2); 3 – (х1, х2); 4 – (х1, х2). | ||
| + | [[Файл:dvovmart.jpg|center|300px]] | ||
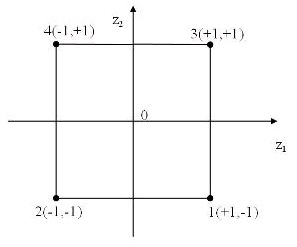
| + | Перехід до безрозмірної (нормалізованої) форми змінних відповідає переходу до нової системи координат з початком у центрі досліджуваної області. Підставивши у формулу перетворення координати точок 1, 2, 3 і 4 дістанемо координати цих точок у новій системі: 1 (+1, – 1); 2 (–1, – 1); 3 (+1, +1); 4 (–1, +1) | ||
| + | [[Файл:dvovmart2.jpg|center|300px]] | ||
| + | Ці координати іноді позначають малими латин¬ськими літерами. Для кодування двофакторного плану вико¬ристовують тільки а і b, а також символ (1). Перша точка позначається літерою а. Це свідчить про те, що на верхньому рівні знаходиться тільки перший фактор. Відповідно b означає, що на рівні +1 є другий фактор. Добуток ab від¬повідає точці 3. Символ (1) використовується для позначення точки з двома факторами на нижньому рівні. | ||
| + | |||
| + | === Матриця планування двофакторного експерименту === | ||
| + | |||
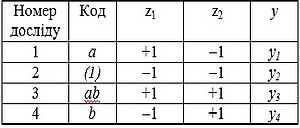
| + | Показані точки по порядку матимуть позначення: а, (1), ab, b. Координати точок записують у вигляді матриці планування експерименту. Матрицю планування разом з результатами експериментів (вектор-стовпцем функції відклику) зображено в таблиці. | ||
| + | [[Файл:dvovmart3.jpg|center|300px]] | ||
| + | |||
| + | ==Трифакторний експеримент== | ||
| + | |||
| + | Матрицю <math>2^2</math> легко перетворити в матрицю <math>2^3</math> іншим способом (повторивши двічі): один раз при новому факторі х3, взятому на нижньому рівні, а другий — при х3 = +1. Утворена матриця може бути зображена рядком (1), а, b, ab, с, ас, bc, abc | ||
| + | [[Файл:dvovmart4.jpg|center|300px]] | ||
| + | Число рядків матриці планування, тобто число дослідів, зростає за показниковою функцією <math>2^n</math>. Далі покажемо, що не всі досліди потребують реалізації, якщо виконуються певні передумови. | ||
| + | |||
| + | ===Матриця планування трифакторного експерименту=== | ||
| + | |||
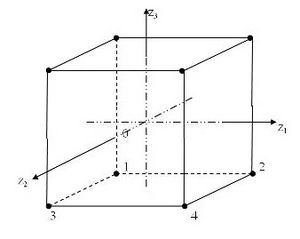
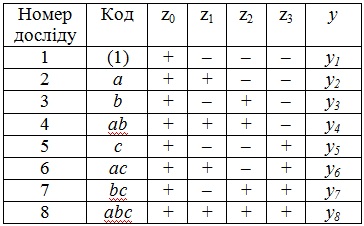
| + | Побудуємо матрицю планування для трифакторної за¬дачі. При цьому слід пам'ятати, що ПФЕ — це весь можли¬вий перебір неповторювальних комбінацій рівнів. Матрицю зручно починати з рядка, де всі керовані змінні перебувають на нижньому рівні, тобто z1 = —1, z2 = —1, z3 = —1. | ||
| + | Наступні рядки (багатовимірні точки) вибирають за прави¬лом: при відрядковому переборі всіх варіантів частота зміни знака керованих змінних для кожної наступної змінної удві¬чі менша, ніж для попередньої. Оскільки всі змінні можуть набувати тільки значень +1 та —1, це дає змогу з метою спрощення записувати в матрицю (таблиця) тільки знаки «+» і «-». Фіктивна змінна z0 по всіх рядках має знак «+». Кількість рядків <math>2^n = 2^3 = 8</math>. | ||
| + | [[Файл:dvovmart5.jpg|center|400px]] | ||
| + | |||
| + | ==Перелік літературних джерел== | ||
| + | #Аністратенко В.О., Федоров В.Г. /Математичне планування експериментів в АПК: Навч. посібник.-К.Вища шк., 1993.-375 с. | ||
| + | #Е.Т. Володарский, Б.Н. Малиновский, Ю.М. Туз-К./Планирование и организация измерительного експреимента:Вища шк.Головное изд-во, 1987.-280 с. | ||
| + | #Федоров В.В. Теория оптимального эксперимента. М.: Наука, 1971. | ||
| + | |||
| + | |||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 08:50, 10 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| Нема | ||
| Імя | Гуменюк | |
| Прізвище | Ірина | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | СН-10-078 | |
Повний факторний експеримент (ПФЕ) – експеримент, що реалізує всі можливі неповторювані комбінації незалежних змінних, кожна з яких примусово (активно) варіює на двох рівнях. Число цих комбінацій при n факторах [math]N = 2^n[/math] і визначає тип планування.
Зміст
Основні відомості
ПФЕ дає можливість знайти роздільні оцінки коефіцієнтів bі. Оскільки використовується поліном першого порядку, то план такого експерименту називають планом першого порядку.
- Знаходження моделі методом ПФЕ складається з:
- планування експерименту;
- власне експерименту;
- перевірки відтворюваності (однорідності вибіркових дисперсій);
- утворення математичної моделі об’єкта з перевіркою статистичної значущості вибіркових коефіцієнтів регресії;
- перевірки адекватності математичного опису.
Двофакторний експеримент
Для двофакторної задачі область факторного простору, що підлягає вивченню, має вигляд прямокутника (рисунок 2) з координатами кутових точок: 1 – (х1, х2); 2 – (х1, х2); 3 – (х1, х2); 4 – (х1, х2).
Перехід до безрозмірної (нормалізованої) форми змінних відповідає переходу до нової системи координат з початком у центрі досліджуваної області. Підставивши у формулу перетворення координати точок 1, 2, 3 і 4 дістанемо координати цих точок у новій системі: 1 (+1, – 1); 2 (–1, – 1); 3 (+1, +1); 4 (–1, +1)
Ці координати іноді позначають малими латин¬ськими літерами. Для кодування двофакторного плану вико¬ристовують тільки а і b, а також символ (1). Перша точка позначається літерою а. Це свідчить про те, що на верхньому рівні знаходиться тільки перший фактор. Відповідно b означає, що на рівні +1 є другий фактор. Добуток ab від¬повідає точці 3. Символ (1) використовується для позначення точки з двома факторами на нижньому рівні.
Матриця планування двофакторного експерименту
Показані точки по порядку матимуть позначення: а, (1), ab, b. Координати точок записують у вигляді матриці планування експерименту. Матрицю планування разом з результатами експериментів (вектор-стовпцем функції відклику) зображено в таблиці.
Трифакторний експеримент
Матрицю [math]2^2[/math] легко перетворити в матрицю [math]2^3[/math] іншим способом (повторивши двічі): один раз при новому факторі х3, взятому на нижньому рівні, а другий — при х3 = +1. Утворена матриця може бути зображена рядком (1), а, b, ab, с, ас, bc, abc
Число рядків матриці планування, тобто число дослідів, зростає за показниковою функцією [math]2^n[/math]. Далі покажемо, що не всі досліди потребують реалізації, якщо виконуються певні передумови.
Матриця планування трифакторного експерименту
Побудуємо матрицю планування для трифакторної за¬дачі. При цьому слід пам'ятати, що ПФЕ — це весь можли¬вий перебір неповторювальних комбінацій рівнів. Матрицю зручно починати з рядка, де всі керовані змінні перебувають на нижньому рівні, тобто z1 = —1, z2 = —1, z3 = —1. Наступні рядки (багатовимірні точки) вибирають за прави¬лом: при відрядковому переборі всіх варіантів частота зміни знака керованих змінних для кожної наступної змінної удві¬чі менша, ніж для попередньої. Оскільки всі змінні можуть набувати тільки значень +1 та —1, це дає змогу з метою спрощення записувати в матрицю (таблиця) тільки знаки «+» і «-». Фіктивна змінна z0 по всіх рядках має знак «+». Кількість рядків [math]2^n = 2^3 = 8[/math].
Перелік літературних джерел
- Аністратенко В.О., Федоров В.Г. /Математичне планування експериментів в АПК: Навч. посібник.-К.Вища шк., 1993.-375 с.
- Е.Т. Володарский, Б.Н. Малиновский, Ю.М. Туз-К./Планирование и организация измерительного експреимента:Вища шк.Головное изд-во, 1987.-280 с.
- Федоров В.В. Теория оптимального эксперимента. М.: Наука, 1971.