Відмінності між версіями «Насадка Борда»
Shkod (обговорення • внесок) |
|||
| (Не показані 5 проміжних версій 3 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | + | '''Насадка Борда'''-(Насадка внутрішня) (рос. насадка внутренняя (Борда); англ. internal mouthpiece (Borda); нім. Inneneinsatz m, Borda-Inneneinsatz m, Innenaufsatz m) – круглоциліндрична насадка, розміщена з внутрішнього боку стінки посудини (або водойми), з якої вона живиться. | |
Насадка Борда використовується для спорожнення резервуарів, коли з конструктивних міркувань не можна встановити [[насадок Вентурі ]]. | Насадка Борда використовується для спорожнення резервуарів, коли з конструктивних міркувань не можна встановити [[насадок Вентурі ]]. | ||
| − | == Історія | + | == Історія виникнення == |
[[Файл:Жан-Шарль_Борда.jpg|thumb|Жан Шарль де Борда]] | [[Файл:Жан-Шарль_Борда.jpg|thumb|Жан Шарль де Борда]] | ||
Внутрішня насадка Борда названа на честь французького вченого, фізика та геодезиста Шарля Жан Борда (4.5.1733, Дакс, — 19.2.1799, Париж)Член Паризької АН. Служив офіцером у армії, потім на флоті. Визначив (1792) довжину секундного маятника в Парижі і знайшов спосіб точного визначення періоду хитання маятника. 1766р. запропонував [[внутрішню насадку]] для збільшення витрати рідини, яка витікає з посудини, при заданому перерізі вихідного отвору. Довів теорему(що носить його ім'я) в гідравліці про удар струменя рідини чи газу. Розробив одну із систем вертикальних осей астрономо-геодезичних інструментів. | Внутрішня насадка Борда названа на честь французького вченого, фізика та геодезиста Шарля Жан Борда (4.5.1733, Дакс, — 19.2.1799, Париж)Член Паризької АН. Служив офіцером у армії, потім на флоті. Визначив (1792) довжину секундного маятника в Парижі і знайшов спосіб точного визначення періоду хитання маятника. 1766р. запропонував [[внутрішню насадку]] для збільшення витрати рідини, яка витікає з посудини, при заданому перерізі вихідного отвору. Довів теорему(що носить його ім'я) в гідравліці про удар струменя рідини чи газу. Розробив одну із систем вертикальних осей астрономо-геодезичних інструментів. | ||
| Рядок 17: | Рядок 17: | ||
Насадка, яка конічно сходиться (конфузор) дає можливість отримувати компактний струмінь, що володіє великою кінетичною енергією. Застосовується в соплах гідравлічних турбін, водострумних і парострумних насосах, гідромоніторах, брандспойти і т. д. Коефіцієнти закінчення для цих насадков залежать від кута конусності. Оптимальним є кут конусності, рівний 13,24': | Насадка, яка конічно сходиться (конфузор) дає можливість отримувати компактний струмінь, що володіє великою кінетичною енергією. Застосовується в соплах гідравлічних турбін, водострумних і парострумних насосах, гідромоніторах, брандспойти і т. д. Коефіцієнти закінчення для цих насадков залежать від кута конусності. Оптимальним є кут конусності, рівний 13,24': | ||
| − | + | ε = 0,982; | |
Насадка, яка конічно розходиться (дифузор) застосовується в ежекторних установках, в димоходах, в аеродинамічних трубах, поливальних машинах, в каналах направляючого апарату насосів, в всмоктуючих трубах насосів і турбін і т. д. Розширення в області стисненого перерізу струменя, що виходить з отвору, дозволяє збільшити так звану вакуумну порожнину. Це дає збільшення витрати до 45-50%. | Насадка, яка конічно розходиться (дифузор) застосовується в ежекторних установках, в димоходах, в аеродинамічних трубах, поливальних машинах, в каналах направляючого апарату насосів, в всмоктуючих трубах насосів і турбін і т. д. Розширення в області стисненого перерізу струменя, що виходить з отвору, дозволяє збільшити так звану вакуумну порожнину. Це дає збільшення витрати до 45-50%. | ||
| − | + | ε = 1; | |
Коноідальний насадок має вхід, виконаний по контурах струменя, який виходить з отвору, тому втрати при русі рідини мінімальні. Він дозволяє майже в півтора рази збільшувати витрати через отвір, і виходящий струмінь має велику кінетичну енергію. Він має велике застосування в соплах гідравлічних турбін, в аеродинамічних трубах, в гідромоніторах, в мірних пристроях. Також використовується для дроблення і різання гірських порід. | Коноідальний насадок має вхід, виконаний по контурах струменя, який виходить з отвору, тому втрати при русі рідини мінімальні. Він дозволяє майже в півтора рази збільшувати витрати через отвір, і виходящий струмінь має велику кінетичну енергію. Він має велике застосування в соплах гідравлічних турбін, в аеродинамічних трубах, в гідромоніторах, в мірних пристроях. Також використовується для дроблення і різання гірських порід. | ||
| Рядок 138: | Рядок 138: | ||
рис.3.Вди внутрішніх насадок | рис.3.Вди внутрішніх насадок | ||
| − | Методи розрахунку подані у таблиці: | + | Методи розрахунку подані у таблиці і графіку: |
[[Файл:2345.png]] | [[Файл:2345.png]] | ||
| + | |||
| + | [[Файл:345.png]] | ||
== Джерела == | == Джерела == | ||
Поточна версія на 12:02, 20 вересня 2020
Насадка Борда-(Насадка внутрішня) (рос. насадка внутренняя (Борда); англ. internal mouthpiece (Borda); нім. Inneneinsatz m, Borda-Inneneinsatz m, Innenaufsatz m) – круглоциліндрична насадка, розміщена з внутрішнього боку стінки посудини (або водойми), з якої вона живиться. Насадка Борда використовується для спорожнення резервуарів, коли з конструктивних міркувань не можна встановити насадок Вентурі .
Зміст
Історія виникнення
Внутрішня насадка Борда названа на честь французького вченого, фізика та геодезиста Шарля Жан Борда (4.5.1733, Дакс, — 19.2.1799, Париж)Член Паризької АН. Служив офіцером у армії, потім на флоті. Визначив (1792) довжину секундного маятника в Парижі і знайшов спосіб точного визначення періоду хитання маятника. 1766р. запропонував внутрішню насадку для збільшення витрати рідини, яка витікає з посудини, при заданому перерізі вихідного отвору. Довів теорему(що носить його ім'я) в гідравліці про удар струменя рідини чи газу. Розробив одну із систем вертикальних осей астрономо-геодезичних інструментів.
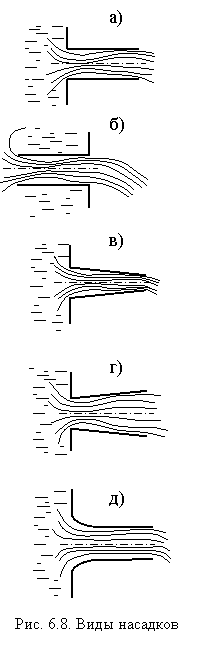
Види насадок і області їх застосування
Насадки (рис. 6.8) за формою патрубка можуть бути циліндричні зовнішні (а) і внутрішні (б), конічні, які сходяться (в) і розходяться (г) і коноідальні, виконані за формою струменя (д). Зовнішній циліндричний насадок (насадок Вентурі) застосовується для збільшення пропускної здатності отвору в якості водоскидних і дренажних труб
Внутрішній циліндричний насадок (насадок Борда) використовується для спорожнення резервуарів, коли з конструктивних міркувань не можна встановити насадок Вентурі:
Насадка, яка конічно сходиться (конфузор) дає можливість отримувати компактний струмінь, що володіє великою кінетичною енергією. Застосовується в соплах гідравлічних турбін, водострумних і парострумних насосах, гідромоніторах, брандспойти і т. д. Коефіцієнти закінчення для цих насадков залежать від кута конусності. Оптимальним є кут конусності, рівний 13,24': ε = 0,982;
Насадка, яка конічно розходиться (дифузор) застосовується в ежекторних установках, в димоходах, в аеродинамічних трубах, поливальних машинах, в каналах направляючого апарату насосів, в всмоктуючих трубах насосів і турбін і т. д. Розширення в області стисненого перерізу струменя, що виходить з отвору, дозволяє збільшити так звану вакуумну порожнину. Це дає збільшення витрати до 45-50%. ε = 1;
Коноідальний насадок має вхід, виконаний по контурах струменя, який виходить з отвору, тому втрати при русі рідини мінімальні. Він дозволяє майже в півтора рази збільшувати витрати через отвір, і виходящий струмінь має велику кінетичну енергію. Він має велике застосування в соплах гідравлічних турбін, в аеродинамічних трубах, в гідромоніторах, в мірних пристроях. Також використовується для дроблення і різання гірських порід.
Витікання рідини через внутрішню насадку
[math]Q={{\mu }_{}}\omega \sqrt{2g{{H}_{c}}}[/math] (1)
де [math]{{H}_{c}}[/math] - напір на рівні центру тяжіння отвору
[math]{{\mu }_{}}[/math] - коефіцієнт витрат великого отвору
Формула (1) і значення [math]{{\mu }_{}}[/math] можуть бути застосовані для отворів будь-якої форми.
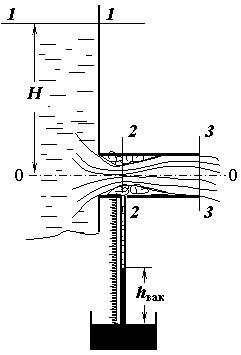
Приєднання насадка до отвору того ж діаметру змінює характер перебігу. Це добре можна показати, застосовуючи рівняння Бернуллі до січень 1-1 і 2-2, а потім 1-1 і 3-3.Як можна бачити на (рис.1), потік рідини в насадці можна розділити на дві зони. Основна частина - це власне струмінь. Течія в області стиснутого перерізу (2-2), нестала. Вона виникає внаслідок того, що при видаленні повітря з цієї області на початку руху, тут утворюється зона розрідження. Величину вакууму легко вимірюють за допомогою вакуумметра будь-якої конструкції. Наявність вакууму всередині насадка, приєднаного до отвору, сприяє додатковому підсосу рідини і збільшення пропускної здатності отвору, що визначається за рівнянням Бернуллі для перерізів 1-1 і 2-2.
[math]{{Z}_{1}}+\frac{P1}{\rho g}+\frac{a1\nu _{1}^{2}}{2g}={{Z}_{2+}}\frac{P2}{\rho g}+\frac{a2\nu _{2}^{2}}{2g}+{{k}_{\omega 1-2}}[/math]
z1=H
p1=pa
[math]\rho[/math]=0
z2=0
p2=pa-[math]\rho[/math]ghвак
[math]hw=hr={{\xi }_{}}\frac{\nu _{c}^{2}}{2g}[/math]
Після підстановки значень визначається величина швидкості витікання через отвір при наявності насадка:
[math]{{H}_{1}}+\frac{{{P}_{a}}}{\rho g}=\frac{{{P}_{a}}}{\rho g}-\frac{\rho g{{h}_{}}}{\rho g}+\frac{a\nu _{c}^{2}}{2g}+{{\xi }_{}}\frac{\nu _{c}^{2}}{2g}[/math]
[math]{{H}_{1}}+{{h}_{}}=\frac{a\nu _{c}^{2}}{2g}+{{\xi }_{}}\frac{\nu _{c}^{2}}{2g}[/math]
[math]{{\nu }_{=\varphi \sqrt{2g(H+{{h}_{}})}}}[/math] (2)
Як можна бачити, відбувається збільшення чинного напору на величину вакууму в області стиснутого перерізу. Якщо підставити значення вакууму для розглянутого зовнішнього циліндричного насадка [math]{{h}_{}}[/math]=0,75Н, то величина швидкості витікання, а, отже, і витрати збільшиться в
[math]\sqrt{1,75}=1,32[/math] рази, тобто на 32%.
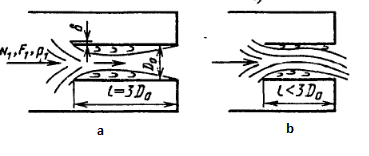
При розгляді перерізів 1-1 і 3-3 будуть отримані формули зі своїми коефіцієнтами. Так, на рис.1 видно, що струмінь на виході з насадка займає весь переріз патрубка, тобто стиск на виході відсутній і коефіцієнт стиснення Eн = 1. У тому випадку, якщо струмінь не доходить до стінок патрубка, вакуум в стислому перерізі не утворюється, насадок не працює, витікання відбувається через отвір, і збільшення витрат немає. Для створення умов роботи насадка його довжина повинна бути не менше трьох розмірів отвору.
Отже, розрахункові формули для насадков мають такий вигляд:
[math]{{a}_{}}=2\varphi \sqrt{2gH}[/math]
[math]{{Q}_{}}={{\mu }_{_{}}}{{\omega }_{}}\sqrt{2gH}[/math]
де [math]{{a}_{}}[/math] - коефіцієнт швидкості для насадка
[math]{{Q}_{}}[/math] - коефіцієнт витрати для насадка.
Так як Eн = 1, то коефіцієнти [math]{{a}_{}}[/math], [math]{{Q}_{}}[/math] рівні між собою. Значення коефіцієнтів залежать від виду насадків.
Для внутрішньої циліндричної насадки [math]{{a}_{}}[/math]=[math]{{Q}_{}}[/math]=0,71
Особливості насадка Борда
Циліндричні насадки зустрічаються у вигляді деталей гідравлічних систем машин і споруд.Характерною особливістю насадка Борда є те, що тиск у стисненому перерізі менший за атмосферний. Це положення доводиться рівнянням Бернуллі, складеним для стисненого і вихідного перерізів,тому значення коефіцієнтів витрати і швидкості менше за значенння коефіцієнтів в зовнішній насадці.Насадок Борда відрізняється від насадка Вентурі тільки умовами входу.Вважають, що довжина насадка Борда повинна бути не менше (3,5-е-4)D. Як видно, для насадка Борда стиснення в перерізі 2-2 виходить більшим, ніж для насадка Вентурі.У зв'язку з цією обставиною втрата напору, а також швидкість і вакуум в перерізі 2-2 для насадка Борда також виходять більшими, ніж для насадка Вентурі (при рівних інших умовах).Легко переконатися, що насадок Борда збільшує витрату рідини, яка витікає з отвору, але трохи меньше, ніж насадок Вентурі. В результаті стиснення струменя в насадці утворюється вакуум і відбувається підсос рідини з резервуара.
Методи розрахунку насадка Борда
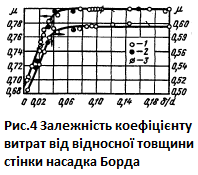
Є декілька підходів до розрахунку насадка Борда,вони повязані з товщиною стінки отвору від якої залежить значення коефіцієнта витрат
рис.3.Вди внутрішніх насадок
Методи розрахунку подані у таблиці і графіку:
Джерела
Мала гірнича енциклопедія. В 3-х т. / За ред. В. С. Білецького. — Донецьк: «Донбас», 2004. — ISBN 966-7804-14-3.
Механика сплошной среды. Т.2 /Седов Л.И.
Идельчик И.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559 с.
Дробинс В. Ф. Гидравлика и гидравлические машины. – М.: Просвещение, 1982.