Відмінності між версіями «Сопла Лаваля»

(Створена сторінка: '''Сопло Лаваля''' — технічне пристосування, яке служить для прискорення газового потоку, …)
 
 
(Не показані 9 проміжних версій 2 користувачів)
Рядок 1: Рядок 1:
 +
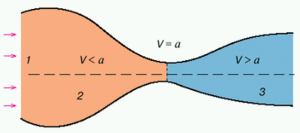
[[Файл:9612 081.2.preview.gif|thumb|Схема течії в соплі Лаваля]]
 +
 
'''Сопло Лаваля''' — технічне пристосування, яке служить для прискорення газового потоку, що проходить по ньому до швидкостей, що перевищують швидкість звуку.
 
'''Сопло Лаваля''' — технічне пристосування, яке служить для прискорення газового потоку, що проходить по ньому до швидкостей, що перевищують швидкість звуку.
 
У найпростішому випадку сопло представляє собою циліндричний або конічний патрубок (насадок), один кінець якого приєднаний до джерела рідини чи газу, а з іншого виходить сформований струмінь.
 
У найпростішому випадку сопло представляє собою циліндричний або конічний патрубок (насадок), один кінець якого приєднаний до джерела рідини чи газу, а з іншого виходить сформований струмінь.
−
[[Файл:9612 081.2.preview.gif]]
+
 
 +
== Історія виникнення сопла Лаваля ==
 +
[[Файл:Карл Густав Патрик де Лаваль.jpeg|thumb|Карл Густав Патрик де Лаваль]]
 +
Карл Густав Патрік де Лаваль (9.5.1845, Орса, - 2.2.1913, Стокгольм), шведський інженер і винахідник. За національністю француз. Закінчив технологічний інститут і університет (1872) в Упсалі. У 1878 році сконструював відцентровий сепаратор безперервної дії (для молока). У 1889 році побудував парову турбіну активного типу. Вперше застосував розширюючі сопла, гнучкий вал, диск рівного опору, що дозволив досягати дуже високих швидкостей (419 м / сек). Крім того, в турбінах Лаваля було передбачено багато нових елементів, частина з яких використовується в сучасному турбобудуванні. Лаваль розробив також теорію сопла. Внаслідок ряду конструктивних недоліків і відносно невеликої потужності турбіни Лаваля не набули поширення, але зіграли важливу роль у розвитку турбобудування.
  
 
==Принцип дії ==
 
==Принцип дії ==
−
'''Сопло Лаваля''' – це комбіноване сопло, яке спочатку звужується, а після розширюється. В самому вузькому місці(найменше січення) завжди встановлюється критична швидкість <math>
 
−
{\omega _{2kp}}
 
−
</math> і максимальна витрата.В розширюючій частині при постійній витраті <math>
 
−
{m_{\max }}
 
−
</math>  швидкість зростає, а її величина визначається з рівняння (1).
 
  
 +
'''Сопло Лаваля''' – це комбіноване сопло, яке спочатку звужується, а після розширюється.
 +
 +
Феномен прискорення газу до надзвукових швидкостей в соплі Лаваля був виявлений в кінці XIX ст. експериментальним шляхом. Пізніше це явище знайшло теоретичне пояснення в рамках газової динаміки.
 +
 +
При наступному аналізі перебігу газу в соплі Лаваля приймаються наступні допущення:
 +
 +
*Газ вважається ідеальним.
 +
*Газовий потік є ізоентропним (тобто має постійну ентропію, сили тертя і дисипативні втрати не враховуються) і адіабатичним (тобто теплота не підводиться і не відводиться).
 +
*Газова течія є стаціонарним і одновимірним, тобто в будь-якій фіксованій точці сопла всі параметри потоку постійні в часі і змінюються тільки уздовж осі сопла, причому у всіх точках обраного поперечного перерізу параметри потоку однакові, а вектор швидкості газу всюди паралельний осі симетрії сопла.
 +
*Масова витрата газу однакова у всіх поперечних перерізах потоку.
 +
*Вісь симетрії сопла є просторовою координатою.
 +
Ставлення локальної швидкості <math>\,v</math> до локальної швидкості звуку '''<math>\, C </math>''' позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати '''<math>\, x </math>''':
 +
<center><math>M = \frac{v}{C}</math>&nbsp;&nbsp;&nbsp;&nbsp;'''(3)'''</center>
 +
 +
З рівняння стану ідеального газу слідує:<math>\frac{dp}{d\rho}=C^2</math>, тут <math>\,\rho</math> - локальна щільність газу, <math>\, p </math> - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера набуває вигляду:
 +
<center><math>
 +
        v\frac{dv}{dx}
 +
      = - \frac{1}{\rho}\cdot \frac{dp}{dx}
 +
      = - \frac{1}{\rho}\cdot \frac{dp}{d\rho}\cdot \frac{d\rho}{dx}
 +
      = - \frac{C^2}{\rho}\cdot \frac{d\rho}{dx}
 +
</math>,</center>
 +
 +
що, враховуючи (3), перетворюється в <math>\frac{1}{\rho}\cdot \frac{d\rho}{dx} = -M^2\cdot \frac{1}{v}\cdot \frac{dv}{dx}</math>. &nbsp;&nbsp;&nbsp;&nbsp;'''(4)'''
 +
 +
Рівняння (4) є ключовим у даному міркуванні.
 +
Розглянемо його в такій формі:<br />
 +
<center><math>\frac{1}{\rho} \frac{d\rho}{dx} / \frac{1}{v} \frac{dv}{dx} = -M^2 </math> &nbsp;&nbsp;&nbsp;&nbsp;'''(4.1)'''</center><br />
 +
Величини <math>\frac{1}{\rho} \frac{d\rho}{dx} </math> и <math>\frac{1}{v} \frac{dv}{dx} </math> характеризують відносну ступінь змінності по координаті <math>\,x</math> щільності газу і його швидкості відповідно. Причому рівняння (4.1) показує, що співвідношення між цими величинами рівне квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність убуває). Таким чином, на дозвукових швидкостях <math>\,(M<1)</math> щільність змінюється в меншій мірі, ніж швидкість, а на надзвукових <math>\,(M>1)</math> - навпаки. Як буде видно далі, це і визначає звужуючу-розширюючу форму сопла.
 +
 +
Оскільки масова витрата газу постійна:
 +
<center><math>\rho\cdot v\cdot A = \mathsf{const}</math>,</center>
 +
где <math>\, A </math> - площа місцевого перетину сопла,
 +
 +
<center><math>\ln \rho + \ln v + \ln A = \ln(\mathsf{const})</math>,</center>
 +
диференціюючи обидві частини цього рівняння по <math>\, x </math>, одержуємо:
 +
<center><math>\frac{1}{\rho}\cdot \frac{d\rho}{dx} + \frac{1}{v}\cdot \frac{dv}{dx} + \frac{1}{A}\cdot \frac{dA}{dx} = 0</math></center>.
 +
Після підстановки з (4) в це рівняння, отримуємо остаточно:
 +
<center><math>\frac{dA}{dx} = \frac{A}{v}\cdot\frac{dv}{dx}\cdot ({M^2 - 1})</math> &nbsp;&nbsp;&nbsp;&nbsp;'''(5)'''</center>
 +
Зауважимо, що при збільшенні швидкості газу в соплі знак вираження <math>\frac{A}{v}\cdot\frac{dv}{dx}</math> позитивний і, отже, знак похідної <math>\frac{dA}{dx}</math>  визначається знаком вираження : <math>\,({M^2 - 1})</math>
 +
 +
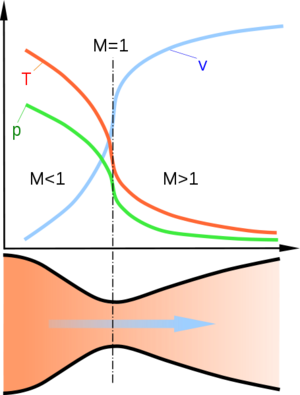
[[Файл:Сопло.png|thumb|Ілюстрація роботи сопла Лаваля. У міру руху газу по соплу, його абсолютна температура Т і тиск Р знижуються, а швидкість V зростає, М - число Маха]]
 +
 +
 +
З чого можна зробити наступні висновки:
 +
*При дозвуковой швидкості руху газу <math>\,(M<1)</math>, похідна <math>\frac{dA}{dx}<0</math>  - сопло звужується.
 +
*При надзвуковій швидкості руху газу <math>\,(M>1)</math>, похідна <math>\frac{dA}{dx}>0</math> - сопло розширюється.
 +
*При русі газу зі швидкістю звуку <math>\,(M = 1)</math>, похідна <math>\frac{dA}{dx}=0</math> - площа поперечного перерізу досягає екстремуму, тобто має місце найвужчий перетин сопла, званий критичним.
 +
 +
Отже, на звуженій, докритичній ділянці сопла рух газу відбувається з дозвуковими швидкостями. У найвужчому, критичному перетині сопла локальна швидкість газу сягає звуковій. На розширеній, закритичній ділянці, газовий потік рухається з надзвуковою швидкістю, прискорюючись. Це прискорення відбувається завдяки тому, що хвиля зниження тиску від розширеної порції газу в надзвуковому потоці не встигає розповсюдитися на наступні за нею інші порції. Закон Бернуллі в цих умовах не виконується. Як наслідок цього, маємо корисну роботу.
 +
 +
==Перше використання сопла Лаваля в ракетному двигуні==
 +
 +
 +
[[Файл:Інженерний тест.jpg|thumb|Надзвуковий струмінь з сопла ракетного двигуна RS-68 на вогневих випробуваннях.]]
 +
 +
В ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні було сопло Лаваля, а з корпусом був пов'язаний кільцевий стабілізатор.
  
−
<math>
 
−
{\omega _2} = \sqrt {2\frac{k}{{k - 1}}} {P_1}{V_1}\left[ {1 - {{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)}^{\frac{{k - 1}}{k}}}} \right]
 
−
</math>  - швидкість потоку
 
  
 +
==Сфера застосування==
  
−
Сопло використовується для раціонального використання енергії потоку при умові, що
+
Широко використовується в парових і газових турбінах, ракетних і повітряно-реактивних двигунах, газодинамічних лазерах, обладнанні для нанесення фарб, абразиво-струминній обробці тощо.
−
<math>
 
−
\frac{{{P_2}}}{{{P_1}}} \triangleleft {\beta _{kp}}
 
−
</math>. Розміри сопла визначаються з рівняння (2) у випадку коли відома витрата 
 
−
m. Спочатку знаходимо площу мінімального січення сопла і його діаметр.
 
  
 +
Залежно від технічного призначення сопла виникають специфічні завдання розрахунку: наприклад, в соплі аеродинамічних труб необхідно забезпечити створення рівномірного і паралельного потоку газу у вихідному перетині, вимоги до сопла ракетних двигунів полягають в здобутті найбільшого імпульсу газового потоку у вихідному перетині сопла при його заданих габаритних розмірах.
  
−
Довжина розширюючої частини визначається: 
+
Ці та інші технічні завдання привели до бурхливого розвитку теорії сопла, що враховує наявність в газовому потоці рідких і твердих часток, нерівноважних хімічних реакцій, перенесення променистої енергії, що зажадало широкого вживання ЕОМ(електронна обчислювальна машина) для вирішення вказаних завдань, а також для розробки складних експериментальних методів дослідження сопла.
−
                                         
 
−
<math>
 
−
l = \frac{{D - d}}{{2tg\frac{\alpha }{2}}}
 
−
</math>, де
 
−
*D – діаметр вихідного січення;
 
−
*d – мінімальний діаметр сопла (у найвужчій частині);
 
−
*α - кут конусності, який вибирають з умови неперервності потоку;
 
−
*α=10-12°
 
−
[[Файл:Безымянный_shf.png‎]]
 
  
 +
==Використана література ==
  
−
==Використання сопла Лаваля==
+
*Абрамович Г. Н., Прикладная газовая динамика, 3 изд., М., 1969: Стернин Л. Е., Основы газодинамики двухфазных течений в соплах, М., 1974.
 +
*Пирумов У.Г. и др., Газовая динамика сопел, М., Наука, 1990
 +
*Ландау Л. Д., Лифшиц Е. М. — Теоретическая физика (Том 6. Гидродинамика). Глава X. Одномерное движение сжимаемого газа. § 97. Истечение газа через сопло.
 +
*Моравский А. В., Файн М. А. — Огонь в упряжке, или Как изобретают тепловые двигатели. — М.: Знание, 1990. (Жизнь замечательных идей). −192 с. ISBN 5-07-000069-1 50000 экз.
 +
*Техническая термодинамика: Учебник для вузов / Под ред. В.И. Крутова, - М.:Высшая школа. 1981. - 439 с.

Поточна версія на 21:32, 21 травня 2012

Схема течії в соплі Лаваля

Сопло Лаваля — технічне пристосування, яке служить для прискорення газового потоку, що проходить по ньому до швидкостей, що перевищують швидкість звуку. У найпростішому випадку сопло представляє собою циліндричний або конічний патрубок (насадок), один кінець якого приєднаний до джерела рідини чи газу, а з іншого виходить сформований струмінь.

Історія виникнення сопла Лаваля

Карл Густав Патрик де Лаваль

Карл Густав Патрік де Лаваль (9.5.1845, Орса, - 2.2.1913, Стокгольм), шведський інженер і винахідник. За національністю француз. Закінчив технологічний інститут і університет (1872) в Упсалі. У 1878 році сконструював відцентровий сепаратор безперервної дії (для молока). У 1889 році побудував парову турбіну активного типу. Вперше застосував розширюючі сопла, гнучкий вал, диск рівного опору, що дозволив досягати дуже високих швидкостей (419 м / сек). Крім того, в турбінах Лаваля було передбачено багато нових елементів, частина з яких використовується в сучасному турбобудуванні. Лаваль розробив також теорію сопла. Внаслідок ряду конструктивних недоліків і відносно невеликої потужності турбіни Лаваля не набули поширення, але зіграли важливу роль у розвитку турбобудування.

Принцип дії

Сопло Лаваля – це комбіноване сопло, яке спочатку звужується, а після розширюється.

Феномен прискорення газу до надзвукових швидкостей в соплі Лаваля був виявлений в кінці XIX ст. експериментальним шляхом. Пізніше це явище знайшло теоретичне пояснення в рамках газової динаміки.

При наступному аналізі перебігу газу в соплі Лаваля приймаються наступні допущення:

  • Газ вважається ідеальним.
  • Газовий потік є ізоентропним (тобто має постійну ентропію, сили тертя і дисипативні втрати не враховуються) і адіабатичним (тобто теплота не підводиться і не відводиться).
  • Газова течія є стаціонарним і одновимірним, тобто в будь-якій фіксованій точці сопла всі параметри потоку постійні в часі і змінюються тільки уздовж осі сопла, причому у всіх точках обраного поперечного перерізу параметри потоку однакові, а вектор швидкості газу всюди паралельний осі симетрії сопла.
  • Масова витрата газу однакова у всіх поперечних перерізах потоку.
  • Вісь симетрії сопла є просторовою координатою.

Ставлення локальної швидкості [math]\,v[/math] до локальної швидкості звуку [math]\, C[/math] позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати [math]\, x[/math]:

[math]M = \frac{v}{C}[/math]    (3)

З рівняння стану ідеального газу слідує:[math]\frac{dp}{d\rho}=C^2[/math], тут [math]\,\rho[/math] - локальна щільність газу, [math]\, p[/math] - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера набуває вигляду:

[math]v\frac{dv}{dx} = - \frac{1}{\rho}\cdot \frac{dp}{dx} = - \frac{1}{\rho}\cdot \frac{dp}{d\rho}\cdot \frac{d\rho}{dx} = - \frac{C^2}{\rho}\cdot \frac{d\rho}{dx}[/math],

що, враховуючи (3), перетворюється в [math]\frac{1}{\rho}\cdot \frac{d\rho}{dx} = -M^2\cdot \frac{1}{v}\cdot \frac{dv}{dx}[/math].     (4)

Рівняння (4) є ключовим у даному міркуванні. Розглянемо його в такій формі:

[math]\frac{1}{\rho} \frac{d\rho}{dx} / \frac{1}{v} \frac{dv}{dx} = -M^2[/math]     (4.1)

Величини [math]\frac{1}{\rho} \frac{d\rho}{dx}[/math] и [math]\frac{1}{v} \frac{dv}{dx}[/math] характеризують відносну ступінь змінності по координаті [math]\,x[/math] щільності газу і його швидкості відповідно. Причому рівняння (4.1) показує, що співвідношення між цими величинами рівне квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність убуває). Таким чином, на дозвукових швидкостях [math]\,(M\lt 1)[/math] щільність змінюється в меншій мірі, ніж швидкість, а на надзвукових [math]\,(M\gt 1)[/math] - навпаки. Як буде видно далі, це і визначає звужуючу-розширюючу форму сопла.

Оскільки масова витрата газу постійна:

[math]\rho\cdot v\cdot A = \mathsf{const}[/math],

где [math]\, A[/math] - площа місцевого перетину сопла,

[math]\ln \rho + \ln v + \ln A = \ln(\mathsf{const})[/math],

диференціюючи обидві частини цього рівняння по [math]\, x[/math], одержуємо:

[math]\frac{1}{\rho}\cdot \frac{d\rho}{dx} + \frac{1}{v}\cdot \frac{dv}{dx} + \frac{1}{A}\cdot \frac{dA}{dx} = 0[/math]
.

Після підстановки з (4) в це рівняння, отримуємо остаточно:

[math]\frac{dA}{dx} = \frac{A}{v}\cdot\frac{dv}{dx}\cdot ({M^2 - 1})[/math]     (5)

Зауважимо, що при збільшенні швидкості газу в соплі знак вираження [math]\frac{A}{v}\cdot\frac{dv}{dx}[/math] позитивний і, отже, знак похідної [math]\frac{dA}{dx}[/math] визначається знаком вираження : [math]\,({M^2 - 1})[/math]

Ілюстрація роботи сопла Лаваля. У міру руху газу по соплу, його абсолютна температура Т і тиск Р знижуються, а швидкість V зростає, М - число Маха


З чого можна зробити наступні висновки:

  • При дозвуковой швидкості руху газу [math]\,(M\lt 1)[/math], похідна [math]\frac{dA}{dx}\lt 0[/math] - сопло звужується.
  • При надзвуковій швидкості руху газу [math]\,(M\gt 1)[/math], похідна [math]\frac{dA}{dx}\gt 0[/math] - сопло розширюється.
  • При русі газу зі швидкістю звуку [math]\,(M = 1)[/math], похідна [math]\frac{dA}{dx}=0[/math] - площа поперечного перерізу досягає екстремуму, тобто має місце найвужчий перетин сопла, званий критичним.

Отже, на звуженій, докритичній ділянці сопла рух газу відбувається з дозвуковими швидкостями. У найвужчому, критичному перетині сопла локальна швидкість газу сягає звуковій. На розширеній, закритичній ділянці, газовий потік рухається з надзвуковою швидкістю, прискорюючись. Це прискорення відбувається завдяки тому, що хвиля зниження тиску від розширеної порції газу в надзвуковому потоці не встигає розповсюдитися на наступні за нею інші порції. Закон Бернуллі в цих умовах не виконується. Як наслідок цього, маємо корисну роботу.

Перше використання сопла Лаваля в ракетному двигуні

Надзвуковий струмінь з сопла ракетного двигуна RS-68 на вогневих випробуваннях.

В ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні було сопло Лаваля, а з корпусом був пов'язаний кільцевий стабілізатор.


Сфера застосування

Широко використовується в парових і газових турбінах, ракетних і повітряно-реактивних двигунах, газодинамічних лазерах, обладнанні для нанесення фарб, абразиво-струминній обробці тощо.

Залежно від технічного призначення сопла виникають специфічні завдання розрахунку: наприклад, в соплі аеродинамічних труб необхідно забезпечити створення рівномірного і паралельного потоку газу у вихідному перетині, вимоги до сопла ракетних двигунів полягають в здобутті найбільшого імпульсу газового потоку у вихідному перетині сопла при його заданих габаритних розмірах.

Ці та інші технічні завдання привели до бурхливого розвитку теорії сопла, що враховує наявність в газовому потоці рідких і твердих часток, нерівноважних хімічних реакцій, перенесення променистої енергії, що зажадало широкого вживання ЕОМ(електронна обчислювальна машина) для вирішення вказаних завдань, а також для розробки складних експериментальних методів дослідження сопла.

Використана література

  • Абрамович Г. Н., Прикладная газовая динамика, 3 изд., М., 1969: Стернин Л. Е., Основы газодинамики двухфазных течений в соплах, М., 1974.
  • Пирумов У.Г. и др., Газовая динамика сопел, М., Наука, 1990
  • Ландау Л. Д., Лифшиц Е. М. — Теоретическая физика (Том 6. Гидродинамика). Глава X. Одномерное движение сжимаемого газа. § 97. Истечение газа через сопло.
  • Моравский А. В., Файн М. А. — Огонь в упряжке, или Как изобретают тепловые двигатели. — М.: Знание, 1990. (Жизнь замечательных идей). −192 с. ISBN 5-07-000069-1 50000 экз.
  • Техническая термодинамика: Учебник для вузов / Под ред. В.И. Крутова, - М.:Высшая школа. 1981. - 439 с.
Отримано з https://wiki.tntu.edu.ua/index.php?title=Сопла_Лаваля&oldid=15734