Відмінності між версіями «Довірчі інтервали»
Shore (обговорення • внесок) |
Mike (обговорення • внесок) м (Відкинуто редагування Долженко Дмитро (обговорення) до зробленого Northfear) |
||
| (Не показано 3 проміжні версії 3 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name= Юрій | Surname= Яскевич| FatherNAme=|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
<center> | <center> | ||
{| | {| | ||
Поточна версія на 01:12, 14 січня 2023
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Юрій | |
| Прізвище | Яскевич | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
|
|
Зміст
Довірчі інтервали та їх межі
Основні положення
Для повного уявлення про точність вимірювань та надійність оцінки випадкових відхилень результатів вимірювань, особливо при обмеженій кількості значень вимірюваної величини, необхідно задатися довірчими межами, довірчим інтервалом та довірчою ймовірністю. Нехай [math]\left( {{x}_{1}},...,{{x}_{n}} \right)\equiv ~x~[/math] - n незалежних спостережень над випадковою величиною з законом розподілу F(z/a), що залежить від параметра a, значення якого невідомо. Довірчі межі випадкових похибок — це верхня та нижня межі інтервалу, в які похибки потрапляють із заданою ймовірністю Р. Величина Р називається довірчою ймовірністю. Для визначення довірчих меж похибок необхідно знати густину розподілу похибок та ймовірність потрапляння похибок у довірчі межі. Якщо не ввести обмеження, то задача матиме множину розв'язків.
- Визначення 1. Функція спостережень a1(x1,...,xn) (помітимо, що це випадкова величина) називається нижньою довірчою границею для параметра a з рівнем довіри РД (звичайно близьким до 1), якщо при будь-якому значенні виконується P
[math]P\{{{a}_{1}}\left( {{x}_{1}},...,{{x}_{n}} \right)\le a\}\ge {{P}_{}}[/math].
- Визначення 2. Функція спостережень a2(x1,...,xn) (випадкова величина) називається верхньою довірчою границею для параметра з рівнем довіри РД , якщо при будь-якім значенні
[math]P\{{{a}_{1}}\left( {{x}_{1}},...,{{x}_{n}} \right)\ge a\}\ge {{P}_{}}[/math].
- Визначення 3. Інтервал з випадковими кінцями (випадковий інтервал)
I(x) = ( a1(x), a2(x) ) , обумовлений двома функціями спостережень, називається довірчим інтервалом для параметра a з рівнем довіри РД , якщо при будь-якім значенні a [math]P\left\{ I\left( x \right)\in a \right\}\equiv P\{~{{a}_{1}}\left( {{x}_{1}},...,{{x}_{n}} \right)\le a\le ~{{a}_{2}}\left( {{x}_{1}},...,{{x}_{n}} \right)\}\ge {{P}_{}}[/math], тобто імовірність ( що залежить від a) накрити випадковим інтервалом I(x) справжнє значення a - більше або дорівнює РД.
Побудова довірчих границь і інтервалівтором
Для побудови довірчого інтервалу (чи границі) необхідно знати закон розподілу статистики [math]\xi =\xi \left( {{x}_{1}},...,{{x}_{n}} \right)~[/math], по якій оцінюється невідомий параметр (такою статистикою може бути оцінка [math]\xi =\hat{a}\left( {{x}_{1}},...,{{x}_{n}} \right)~[/math]). Один зі способів побудови полягає в наступному. Припустимо, що деяка випадкова величина [math]\varphi =\varphi (\xi ,\text{ }a)~~[/math], що залежить від статистики [math]\xi[/math] і невідомого параметра a така, що:
- закон розподілу відомий і не залежить від a;
- [math]\varphi (\xi ,\text{ }a)~~~[/math] є неперервною та монотонною по .
Виберемо діапазон для [math]\varphi ~~[/math] інтервал [math]({{f}_{1}},{{f}_{2}})[/math] так, щоб влучення в нього було практично вірогідно: [math]P\{\text{ }f1\le \varphi (\xi ,\text{ }a)\le f2\text{ }\}\ge P~[/math] для чого досить у якості [math]~f1~,f2[/math] взяти квантилі розподілу [math]\varphi[/math] рівня (1- РД )/2 і (1+ РД )/2 відповідно. Перейдемо в до іншого запису випадкової події. Розв’язуючи нерівності щодо параметра a, одержимо (думаючи, що [math]\varphi[/math] монотонно зростає по a): [math]\text{P}\{\text{ g}(\xi ,\text{ f1})\le \text{a}\le \text{g}(\xi ,\text{ f2})\text{ }\}\ge \text{P}[/math]. Це співвідношення вірне при будь-якім значенні параметра a, і тому, відповідно до визначення, випадковий інтервал [math](g(\xi ,\text{ }{{f}_{1}}),\text{ }g(\xi ,\text{ }{{f}_{2}}))[/math] є довірчим для a з рівнем довіри РД . Якщо [math]\varphi[/math] спадає по a, інтервалом є [math](g(\xi ,\text{ }{{f}_{2}}),g(\xi ,\text{ }{{f}_{1}})\text{ })[/math]. Для побудови однобічної границі для a виберемо значення [math]f1,f2[/math] так, щоб [math]~~~~~~\text{P}\{\varphi (\xi ,a)\ge {{f}_{1}}\}\ge {{P}_{}},~~~~~{{f}_{1}}=Q\left( 1\text{ }-\text{ }{{P}_{}} \right)[/math] чи [math]\text{P}\{\varphi (\xi ,a)\le {{f}_{2}}\}\ge {{P}_{~}}{{,}_{~~~~}}~{{f}_{2}}=\text{ }Q\left( {{P}_{}} \right)[/math] де [math]Q(P)[/math] - квантиль рівня [math]P[/math]. Після розв’язання нерівності одержимо однобічні довірчі границі для a.
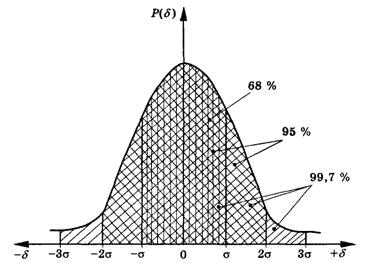
Для звичайних технічних вимірювань, коли не вимагається високий ступінь надійності та точності, довірча ймовірність береться у межах 0,9—0,95. Виходячи з нормального закону розподілу, можна розраховувати ймовірність виникнення випадкових похибок з різними значеннями.
Рівень довіри
Рівень довіри РД означає, що правило визначення інтервалу дає вірний результат з імовірністю РД, що звичайно вибирається близькою до 1, однак, 1 не дорівнює. Переконаємося статистично на прикладі в тім, що довірчий інтервал з рівнем довіри РД може не містити (з малою імовірністю 1- РД ) істинне значення параметру.
- Приклад. Розглянемо наведений випадковий інтервал I(x1, ..., xn), що при будь-якім значенні а накриває це значення з великою імовірністю РД:
Р{ I(x1,...,xn) є a } = РД , і тому, якщо знехтувати можливістю здійснення події [math]a\notin I[/math], що має малу імовірність (1- РД), можна вважати подія [math]a\in I\left( {{x}_{1}},...,{{x}_{n}} \right)[/math] є практично достовірною, тобто можна вірити тому, що обчислений за конкретними спостереженнями x1,...,xn інтервал I містить невідоме значення параметра а. Проведемо випробування інтервалу на 50 вибірках обсягу n=10 для трьох рівнів довіри РД : 0.9 , 0.99 , 0.999 (відповідно, три значення fp) . При РД = 0.9 число невірних з k =50 результатів виявиться в околиці 5, тому що середнє число невірних k(1- РД) = 5. При РД =0.99 поява хоча б одна невірного з k =50 досить ймовірна: імовірність цієї події [math]1-\text{ }{{}_{\mathbf{}}}^{k}=1-{{0.99}^{50}}\approx 0.61.[/math]. При РД =0.999 поява хоча б одна невірного є сумнівною: імовірність цієї події [math]1-\text{ }{{}_{\mathbf{}}}^{k}=1-{{0.999}^{50}}\approx 0.05[/math].
Список використаних джерел
- Клепиков Н.П., Соколов С.Н. Анализ и планирование экспериментов методом максимума подобия. М.: Наука, 1964.
- Федоров В.В. Теория оптимального эксперимента. М.: Наука, 1971.
- http://window.edu.ru/window_catalog/pdf2txt?p_id=1180&p_page=1 – Основи планування експериментів (Січень 2010);
- http://uk.wikipedia.org/wiki/Планування_експерименту – Планування експерименту (Січень 2010);
- http://www.refine.org.ua/pageid-4881-4.html – Методи досліджень (Січень 2010).

- Студент: Користувач:Hek
- Виступ відбувся: 11 березня 2010
- Тема: Довірчі інтервали та їх межі.