Відмінності між версіями «Моделювання об'єкту»
Віктор (обговорення • внесок) |
|||
| (Не показані 11 проміжних версій 6 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name=Віктор | Surname=Проць | FatherNAme=|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
| + | |||
{| cellspacing="0" cellpadding="0" style="clear: {{{clear|right}}}; margin-bottom: .5em; float: right; padding: .5em 0 .8em 1.4em; background: none; width: {{{width|{{{1|auto}}}}}};" {{#if:{{{limit|}}}|class="toclimit-{{{limit}}}"}} | {| cellspacing="0" cellpadding="0" style="clear: {{{clear|right}}}; margin-bottom: .5em; float: right; padding: .5em 0 .8em 1.4em; background: none; width: {{{width|{{{1|auto}}}}}};" {{#if:{{{limit|}}}|class="toclimit-{{{limit}}}"}} | ||
| __TOC__ | | __TOC__ | ||
| Рядок 5: | Рядок 7: | ||
<noinclude> | <noinclude> | ||
| + | |||
| + | |||
| + | =МОДЕЛЮВАННЯ ОБ'ЄКТУ І ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ= | ||
Одним з головних завдань експерименту є здобуття і перевірка математичної моделі об'єкту, взаємозв'язку, що описує в кількісній формі, між вхідними і вихідними параметрами об'єкту. Вхідні параметри, які можуть бути змінені, називають чинниками. Для кожного чинника до виміру встановлюється область визначення, яка може бути безперервною і дискретною. Часто безперервна область визначення штучно дискретизує. У теорії планерування експерименту об'єкт досліджень прийнято представляти у вигляді «чорного ящика», а його математична модель описує функціональні зв'язки між вхідними і вихідними параметрами. Головними вимогами, що пред'являються до математичних моделей об'єктів є зручність математичного використання і інтерпретується моделі. Крім того, завжди мають бути позначені межі застосовності моделі. Якщо ці вимоги не виконуються, то при використанні і експериментальній перевірці моделей неминуче виникають методичні погрішності, і погрішності адекватності, які будуть розглянуті в наступній главі. | Одним з головних завдань експерименту є здобуття і перевірка математичної моделі об'єкту, взаємозв'язку, що описує в кількісній формі, між вхідними і вихідними параметрами об'єкту. Вхідні параметри, які можуть бути змінені, називають чинниками. Для кожного чинника до виміру встановлюється область визначення, яка може бути безперервною і дискретною. Часто безперервна область визначення штучно дискретизує. У теорії планерування експерименту об'єкт досліджень прийнято представляти у вигляді «чорного ящика», а його математична модель описує функціональні зв'язки між вхідними і вихідними параметрами. Головними вимогами, що пред'являються до математичних моделей об'єктів є зручність математичного використання і інтерпретується моделі. Крім того, завжди мають бути позначені межі застосовності моделі. Якщо ці вимоги не виконуються, то при використанні і експериментальній перевірці моделей неминуче виникають методичні погрішності, і погрішності адекватності, які будуть розглянуті в наступній главі. | ||
| Рядок 30: | Рядок 35: | ||
Чотириполюсник складається з двох простих схем: | Чотириполюсник складається з двох простих схем: | ||
| − | 1.детектора на діоді | + | 1.детектора на діоді 'Д' з вихідним резистором <math>{{R}_{1}}</math>. |
| − | 2.інтегруючому ланцюгу. | + | 2.інтегруючому ланцюгу <math>{{R}_{2}}C</math>. |
[[Файл:1.2.png|thumb|center|приклад моделювання простого чотириполюсника]] | [[Файл:1.2.png|thumb|center|приклад моделювання простого чотириполюсника]] | ||
<center>Рис.1.2 - приклад моделювання простого чотириполюсника </center> | <center>Рис.1.2 - приклад моделювання простого чотириполюсника </center> | ||
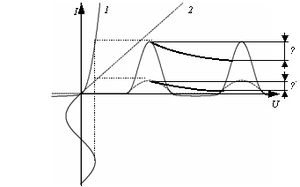
| − | Сигнали на виході детектора АВ і виході інтегруючого ланцюга показані на рис.1.3. Тут криві 1 і 2 відповідають різним вольтамперным характеристикам (ВАХ) діода. Детектор відрізує негативні напівперіоди сигналу, а інтегруючий ланцюг – виділяє ту, що його огинає. Якість виділення що огинає визначатиметься відхиленням | + | Сигнали на виході детектора АВ і виході інтегруючого ланцюга показані на рис.1.3. Тут криві 1 і 2 відповідають різним вольтамперным характеристикам (ВАХ) діода. Детектор відрізує негативні напівперіоди сигналу, а інтегруючий ланцюг – виділяє ту, що його огинає. Якість виділення що огинає визначатиметься відхиленням <math>\Delta </math> від «ідеального» сигналу. |
[[Файл:1.3.png|thumb|center|Сигнали на виході детектора АВ і виході інтегруючого ланцюга ]] | [[Файл:1.3.png|thumb|center|Сигнали на виході детектора АВ і виході інтегруючого ланцюга ]] | ||
<center>Рис.1.3 - Сигнали на виході детектора АВ і виході інтегруючого ланцюга </center> | <center>Рис.1.3 - Сигнали на виході детектора АВ і виході інтегруючого ланцюга </center> | ||
| − | Величина | + | Величина <math>\Delta </math>у свою чергу залежить від характеристик, як детектора, так і інтегруючого ланцюга. У детекторі вона визначатиметься вольтамперной характеристикою (ВАХ) діода 'Д', а в інтегруючому ланцюзі - співвідношенням між ємкістю конденсатора <math>C</math> і опором <math>{{R}_{2}}</math>. |
| − | Як видно з рис.1.3, амплітуда вихідного сигналу детектора, відповідна ВАХ-1, вище, що неминуче приведе до збільшення | + | Як видно з рис.1.3, амплітуда вихідного сигналу детектора, відповідна ВАХ-1, вище, що неминуче приведе до збільшення <math>\Delta </math> в результуючому сигналі. З іншого боку, зменшення ємкості конденсатора інтегруючого ланцюга також наводить до збільшення <math>\Delta </math>. При моделюванні схеми неспівпадання між розрахунковими і реальними сигналами вимагає внесення коректування до характеристик, що задаються в моделі. |
| + | |||
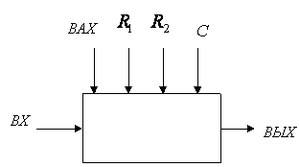
У загальному випадку чотириполюсник може розглядатися як об'єкт, схема якого показана на рис.1.4. Характеристики окремих елементів схеми (ВАХ діода і величини останніх пасивних елементів) можуть вважатися фіксованими параметрами (керівниками). Залежно від плану експерименту ці параметри можна розглядати і як вхідні (чинники), які задаються дискретно. | У загальному випадку чотириполюсник може розглядатися як об'єкт, схема якого показана на рис.1.4. Характеристики окремих елементів схеми (ВАХ діода і величини останніх пасивних елементів) можуть вважатися фіксованими параметрами (керівниками). Залежно від плану експерименту ці параметри можна розглядати і як вхідні (чинники), які задаються дискретно. | ||
[[Файл:1.4.png|thumb|center|схема чотириполюсника]] | [[Файл:1.4.png|thumb|center|схема чотириполюсника]] | ||
| Рядок 51: | Рядок 57: | ||
Експериментальні виміри прийнято розділяти на три основні види: | Експериментальні виміри прийнято розділяти на три основні види: | ||
| − | 1)прямі виміри, при яких безпосередньо реєструються значення вимірюваної величини (наприклад, вимір напруги | + | 1)прямі виміри, при яких безпосередньо реєструються значення вимірюваної величини (наприклад, вимір напруги <math>U</math> вольтметром); |
| − | 2)непрямі виміри (наприклад, виміри сили струму | + | 2)непрямі виміри (наприклад, виміри сили струму <math>I</math> амперметром, активного опору <math>R</math> омметром і розрахунок <math>U=RI</math>); |
| − | Тобто непрямі виміри — це здобуття величини | + | Тобто непрямі виміри — це здобуття величини <math>y=f({{x}_{1}},{{x}_{2}},...)</math> по виміряних значеннях <math>{{x}_{1}},{{x}_{2}},...</math>. |
| − | 3)спільні виміри (наприклад, виміри напруги | + | 3)спільні виміри (наприклад, виміри напруги <math>U</math> і сили струму <math>I</math> при різних значеннях <math>I</math> і побудова результуючої залежності <math>U=U(I)</math>); |
Тобто спільні виміри — це виміри два або декількох неоднойменних величин для побудови залежності між ними. | Тобто спільні виміри — це виміри два або декількох неоднойменних величин для побудови залежності між ними. | ||
Планерування експерименту передбачає не лише оптимізацію числа вимірів, але і зменшення експериментальних погрішностей. Тому значну частину математичного апарату теорії планерування експерименту складають теорія помилок, теорія вірогідності і математична статистика. | Планерування експерименту передбачає не лише оптимізацію числа вимірів, але і зменшення експериментальних погрішностей. Тому значну частину математичного апарату теорії планерування експерименту складають теорія помилок, теорія вірогідності і математична статистика. | ||
| + | |||
| + | =Перелік використаної літератури= | ||
| + | http://www.chuvsu.ru/~rte/uits/liter_uits/plan_exp/glav1_1.htm - МОДЕЛЮВАННЯ ОБ'ЄКТУ І ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ (березень 2010) | ||
Поточна версія на 10:10, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Віктор | |
| Прізвище | Проць | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
МОДЕЛЮВАННЯ ОБ'ЄКТУ І ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ
Одним з головних завдань експерименту є здобуття і перевірка математичної моделі об'єкту, взаємозв'язку, що описує в кількісній формі, між вхідними і вихідними параметрами об'єкту. Вхідні параметри, які можуть бути змінені, називають чинниками. Для кожного чинника до виміру встановлюється область визначення, яка може бути безперервною і дискретною. Часто безперервна область визначення штучно дискретизує. У теорії планерування експерименту об'єкт досліджень прийнято представляти у вигляді «чорного ящика», а його математична модель описує функціональні зв'язки між вхідними і вихідними параметрами. Головними вимогами, що пред'являються до математичних моделей об'єктів є зручність математичного використання і інтерпретується моделі. Крім того, завжди мають бути позначені межі застосовності моделі. Якщо ці вимоги не виконуються, то при використанні і експериментальній перевірці моделей неминуче виникають методичні погрішності, і погрішності адекватності, які будуть розглянуті в наступній главі.
Можна виділити наступні завдання перевірки моделей (рис.1.1):
1.Побудувати «чорний ящик», який буде потрібним чином відгукуватися на задану вхідну дію.
2.Маючи «чорний ящик», знаючи вхідні і вихідні сигнали, отримати (змоделювати) його вміст.
Суть процесу моделювання можна пояснити на прикладі аналізу електронної схеми, в результаті якого будуть отримані певні вихідні сигнали. Можна перевірити модель, зібравши експериментальну схему і знявши реальні вихідні сигнали. При цьому неминучі розбіжності між сигналами модельними і реальними. Аби з'ясувати причини розбіжності, необхідні експерименти з окремими елементами схеми.
Необхідне коректування моделі може бути виконане таким чином:
1.Перевірка розбіжностей — експериментальна перевірка характеристик всіх елементів і їх порівняння з модельними.
2.Виправлення характеристик окремих елементів у вихідній моделі.
3.Зіставлення отриманих залежностей з експериментальними (початковими).
Таким чином, побудова і перевірка моделі, адекватно електронної схеми, що описує роботу, в загальному випадку вимагає дуже великої кількості експериментальних вимірів. Планерування експерименту дозволяє оптимізувати число вимірів. Наприклад, електронна схема складається з транзисторів, резисторів, конденсаторів і котушок індуктивності. Якщо номінальні значення пасивних електронних елементів (резисторів, конденсаторів і т.д) збігаються з їх реальними значеннями з необхідною точністю, то неспівпадання між модельними і реальними сигналами найчастіше виникає із-за невідповідності реальних робочих характеристик активних елементів (транзисторів, мікросхем і так далі). Тому дослідні схемотехніки піддають перевірці лише окремі вузли схеми, по суті інтуїтивно плануючи експеримент виходячи зі свого досвіду і використовуючи апріорну інформацію. Розглянемо приклад моделювання простого чотириполюсника, що здійснює виділення що огинає (детектування) радіосигналу (рис.1.2). Чотириполюсник складається з двох простих схем:
1.детектора на діоді 'Д' з вихідним резистором [math]{{R}_{1}}[/math].
2.інтегруючому ланцюгу [math]{{R}_{2}}C[/math].
Сигнали на виході детектора АВ і виході інтегруючого ланцюга показані на рис.1.3. Тут криві 1 і 2 відповідають різним вольтамперным характеристикам (ВАХ) діода. Детектор відрізує негативні напівперіоди сигналу, а інтегруючий ланцюг – виділяє ту, що його огинає. Якість виділення що огинає визначатиметься відхиленням [math]\Delta[/math] від «ідеального» сигналу.
Величина [math]\Delta[/math]у свою чергу залежить від характеристик, як детектора, так і інтегруючого ланцюга. У детекторі вона визначатиметься вольтамперной характеристикою (ВАХ) діода 'Д', а в інтегруючому ланцюзі - співвідношенням між ємкістю конденсатора [math]C[/math] і опором [math]{{R}_{2}}[/math].
Як видно з рис.1.3, амплітуда вихідного сигналу детектора, відповідна ВАХ-1, вище, що неминуче приведе до збільшення [math]\Delta[/math] в результуючому сигналі. З іншого боку, зменшення ємкості конденсатора інтегруючого ланцюга також наводить до збільшення [math]\Delta[/math]. При моделюванні схеми неспівпадання між розрахунковими і реальними сигналами вимагає внесення коректування до характеристик, що задаються в моделі.
У загальному випадку чотириполюсник може розглядатися як об'єкт, схема якого показана на рис.1.4. Характеристики окремих елементів схеми (ВАХ діода і величини останніх пасивних елементів) можуть вважатися фіксованими параметрами (керівниками). Залежно від плану експерименту ці параметри можна розглядати і як вхідні (чинники), які задаються дискретно.
Експериментальні виміри прийнято розділяти на три основні види:
1)прямі виміри, при яких безпосередньо реєструються значення вимірюваної величини (наприклад, вимір напруги [math]U[/math] вольтметром);
2)непрямі виміри (наприклад, виміри сили струму [math]I[/math] амперметром, активного опору [math]R[/math] омметром і розрахунок [math]U=RI[/math]); Тобто непрямі виміри — це здобуття величини [math]y=f({{x}_{1}},{{x}_{2}},...)[/math] по виміряних значеннях [math]{{x}_{1}},{{x}_{2}},...[/math].
3)спільні виміри (наприклад, виміри напруги [math]U[/math] і сили струму [math]I[/math] при різних значеннях [math]I[/math] і побудова результуючої залежності [math]U=U(I)[/math]); Тобто спільні виміри — це виміри два або декількох неоднойменних величин для побудови залежності між ними.
Планерування експерименту передбачає не лише оптимізацію числа вимірів, але і зменшення експериментальних погрішностей. Тому значну частину математичного апарату теорії планерування експерименту складають теорія помилок, теорія вірогідності і математична статистика.
Перелік використаної літератури
http://www.chuvsu.ru/~rte/uits/liter_uits/plan_exp/glav1_1.htm - МОДЕЛЮВАННЯ ОБ'ЄКТУ І ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ (березень 2010)