Відмінності між версіями «Планування другого порядку»
Ihor p (обговорення • внесок) |
|||
| (Не показані 9 проміжних версій 7 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name=Ігор | Surname=Пельц | FatherNAme= |Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
http://elartu.tstu.edu.ua/handle/123456789/415 Презентація доповіді (університетський репозиторій). | http://elartu.tstu.edu.ua/handle/123456789/415 Презентація доповіді (університетський репозиторій). | ||
Поточна версія на 10:03, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Ігор | |
| Прізвище | Пельц | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
http://elartu.tstu.edu.ua/handle/123456789/415 Презентація доповіді (університетський репозиторій).
Зміст
Планування другого порядку
Планування другого порядку застосовується для математичного опису об'єкта поблизу екстремальної точки статистичної характеристики або тоді, коли необхідний точніший опис в інших точках факторного простору. При цьому використовують поліном другого порядку:
[math]\operatorname{y}={{a}_{0}}+\sum\limits_{i=1}^{n}{{{a}_{i}}{{x}_{i}}+}\sum\limits_{i=1}^{n}{{{a}_{ij}}{{x}_{i}}{{x}_{j}}+}...+\sum\limits_{i=1}^{n}{{{a}_{i,i}}x_{i}^{2}}[/math]
Задача, як і в ПФЕ, полягає у визначенні методом найменших квадратів за результатами спланованого експерименту коефіцієнтів цього рівня за умови, що виконуються передумови регресійного аналізу. ПФЕ типу [math]2^n[/math] дає змогу дістати роздільні оцінки як лінійних коефіцієнтів bi (після переходу до безрозмірних z), так і коефіцієнтів парних взаємодій bij. Точки ПФЕ лежать у вершині n-вимірного куба. Вектор-стовпці лінійних факторів матриці планування ортогональні між собою, тобто виконується умова
[math]\sum\limits_{g=1}^{N}{{{z}_{gi}}{{z}_{gj}}=0;i\ne j.}[/math]
З теорії інтерполяції (апроксимації) відомо, що для розв'язання задачі знаходження роздільних оцінок параметрів апроксимуючого виразу число рівнів для кожної із змінних повинно бути на одиницю більше ступеня апроксимуючого полінома, тобто для полінома другого порядку число рівнів дорівнює трьом. Однак, як показали дослідження, ПФЕ типу [math]3^n[/math] (планування на трьох рівнях) не є раціональним через велике число дослідів. Задача розв'язується іншим способом. До ПФЕ типу [math]2^n[/math] додають центральну точку з координатами (0, 0, ..., 0) і зіркові точки з координатами (0, 0, ..., ±α), які лежать на сфері діаметра 2α (рис. 1). Зіркові точки будують на осях факторного простору. Вибір відстані від нульової точки до зіркової, яка визначається плечем α, залежить від критерію оптимальності плану.
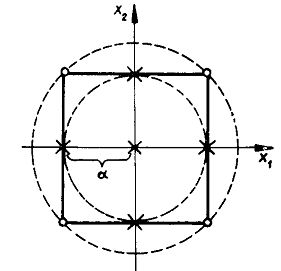
Розглянемо планування, оптимальне з точки зору незалежності оцінок bi,i Його називають ортогональним центральним композиційним плануванням (ОЦКП), тобто планом, в якому критерієм оптимальності є ортогональність стовпців матриці планування. Композиційним таке планування, як й інші форми планування другого порядку, називається тому, що новий план дістають шляхом компонування первинного двофакторного плану з деякою кількістю додаткових точок. Оскільки в числі цих додаткових точок обов'язково фігурує центральна, в якій всі змінні хi мають середній рівень, а zi=0, плани називають центральними. Ортогональність матриці композиційного планування забезпечується виконанням рівностей
[math]\sum\limits_{g=1}^{N}{z_{g,o}^{2}z_{y,i}^{2}=0,\sum\limits_{g=1}^{N}{z_{gi}^{2}z_{gj}^{2}=0,i\ne j}.}[/math]
де і-номер фактора; j-номер рядка; g-номер досліду. Для ортогоналізації першого з цих співвідношень застосовується перехід до нової змінної
[math]\overset{-}{z}\,_{i}^{2}=z_{i}^{2}-\frac{\sum{z_{gi}^{2}}}{N}=z_{i}^{2}-\overset{-}{z}\,_{i}^{2}[/math]
де N-загальне число експериментів. Величина zi залежить тільки від числа факторів n і числа дослідів N, яке звичайно вибирається так, що
[math]\operatorname{N}={{N}_{n}}+{{N}_{a}}+{{N}_{0}}={{2}^{n}}+2n+1,[/math]
де Nn = [math]2^n[/math]-кількість вершин гіперкуба при ПФЕ; Nα = 2n-число зіркових точок; N0= 1- число дослідів у центрі плану. Якщо N вибрати так, то zi визначають за формулою
[math]\operatorname{z}_{i}^{2}=\frac{{{2}^{n}}+2{{\alpha }^{2}}}{N}.[/math]
Тому ортогоналізація другої з вищенаведених умов досягається вибором бажаного α. Для зручності підготовки і планування величини α, N, Nn, Nα обчислені і табульовані залежно від числа факторів (табл. 1).
| n | [math]{{\operatorname{N}}_{0}}[/math] | [math]{{\operatorname{N}}_{n}}[/math] | [math]{{\operatorname{N}}_{\alpha }}[/math] | N | [math]\alpha[/math] |
|---|---|---|---|---|---|
| 2 | 1 | 4 | 2 | 9 | 1,000 |
| 3 | 1 | 8 | 6 | 15 | 1,215 |
| 5 | 1 | 16 | 8 | 25 | 1,414 |
| 5 | 1 | 32 | 10 | 43 | 1,596 |
| 6 | 1 | 64 | 12 | 77 | 1,706 |
| 7 | 1 | 128 | 14 | 143 | 1,909 |
Сформуємо матриці ОЦКП для двох факторів. При n = 2 отримаємо α = 1,0 (див. табл. 1), для обчислення скористаємося наведеними формулами. Оскільки [math]z1^2=(4+2)/9=0,667[/math], то стовпець добувається відніманням одного і того ж числа 0,67 від числа стовпця [math]zi^2[/math] того ж рядка (табл. 2).
| Дослід | j | [math]z_0[/math] | [math]z_1[/math] | [math]z_2[/math] | [math]z_1^2[/math] | [math]z_2^2[/math] | [math]z_{1c}^2[/math] | [math]z_{2c}^2[/math] | [math]z_1*z_2[/math] |
|---|---|---|---|---|---|---|---|---|---|
| Вершини квадрата | |||||||||
| Зіркові точки | |||||||||
| Центр |
Реалізація експериментів за ОЦКП здійснюється за тією ж методикою, що і ПФЕ. Таким чином, через випадковий характер зміни вихідної величини у у кожній точці хg проводиться m паралельних дослідів і обчислюється середнє значення функції відклику
Перед реалізацією проводиться рандомізація рядків матриці планування. Перевірка відтворюваності, як і в ПФЕ, виконується за критерієм Кохрена, після чого обчислюється оцінка дисперсії відтворюваності
[math]S_{y}^{2}=S_{vidtv}^{2}=\frac{\sum\limits_{g=1}^{N}{S_{g}^{2}}}{N}.[/math]
Методика утворення математичної моделі незначно відрізняється від методики опису результатів ПФЕ. Коефіцієнти регресії при ОЦКП обчислюються за формулою
У цьому плануванні оцінки дисперсій коефіцієнтів bi (точність їхнього обчислення) не однакові, оскільки не однаковий знаменник у формулі дисперсії
В ПФЕ знаменник однаковий і дорівнює mN. Це істотний недолік ОЦКП, і тому часто надають перевагу складнішому за обчислювальними процедурами рототабельному плануванню.
Рототабельне планування
У зв'язку з тим, що дисперсії коефіцієнтів рівняння регресії при ОЦКП нерівномірні, ортогональність матриці часто не є досить сильним критерієм оптимальності планування другого порядку. Його заміняють критерієм ротоптабельності, тобто однаковості дисперсій коефіцієнтів при повороті координатних осей на будь-який кут. Зазначимо, що при плануванні першого порядку ортогональність матриці просто збігається з її рототабельністю, тому ПФЕ доцільно називати рототабельним. Щоб зробити план другого порядку рототабельним, вибирають для сфери, на якій розташовуються зіркові точки, радіус (зіркове плече) за формулою
Інша умова рототабельності — збільшення числа дослідів на поверхні нульової сфери, тобто в центрі плану. У зв'язку з цим виникає повна назва методу: центральне композиційне рототабельне планування (ЦКРП). Таким чином ЦКРП багато в чому нагадує ортогональне планування, проте метод рототабельного планування експерименту дає змогу дістати точніший математичний опис поверхні відклику порівняно з ОЦКП, завдяки збільшенню числа дослідів у центрі плану і спеціальному вибору величини зіркового плеча α. Як і для ОЦКП, основні характеристики матриць рототабельного планування табульовані (табл. 3). Позначення тут ті самі, що і для ОЦКП (див. табл. 2). При ЦКРП, починаючи з n = 5, можна застосувати ДФЕ(дробовий факторний експеримент).
| n | [math]{{\operatorname{N}}_{n}}[/math] | [math]{{\operatorname{N}}_{\alpha }}[/math] | [math]{{\operatorname{N}}_{0}}[/math] | N | [math]\alpha[/math] |
|---|---|---|---|---|---|
| 2 | 5 | 4 | 4 | 13 | 1,414 |
| 3 | 6 | 8 | 6 | 20 | 1,680 |
| 4 | 7 | 16 | 8 | 31 | 2,000 |
| 5 | 10 | 32 | 10 | 52 | 2,378 |
| 6 | 15 | 64 | 12 | 91 | 1,828 |
| 7 | 21 | 128 | 14 | 163 | 1,333 |
При рототабельному плануванні для обчислення коефіцієнтів моделі і відповідних оцінок дисперсій знаходять спеціальні комплекси:
де n-число факторів; N-загальне число дослідів у плануванні; N0-число дослідів у центрі плану. За результатами експериментів обчислюють такі суми:
Коефіцієнти моделі тут розраховують за формулами
Оцінки дисперсій для обчислених коефіцієнтів знаходять за такими формулами:
У цих формулах дисперсія відтворюваності [math]S_{y}^{2}[/math] визначається за результатами дослідів у нульовій точці
Дисперсія адекватності оцінюється за формулою
якшо число ступенів вільності
Приклад
Скласти матрицю ЦКРП на прикладі побудови математичної моделі технологічного процесу крупоутворення (див.: Пищевая технология.— 1976.— № 4.— С. 121—124).
Розв'язання. Як функції відклику прийнято [math]y_1[/math], % — середня зольність крупи пшениці після перших трьох систем для дертя (швидкість обертання рифлених вальців усіх систем 6 м/с); [math]y_2[/math], % — сумарний вихід всіх крупок, які добуваються в процесі крупоутворення; [math]y_3[/math], кДж/(кг • %) — витрата енергії на одержання 1 % продукту з 1 кг зерна. Незалежними змінними є, %: [math]x_1[/math] — вихід крупи на першій системі для дертя; [math]x_2[/math] — те ж на другій системі; [math]x_3[/math] — те ж, для трьох систем для дертя. Інтервал варіювання для всіх [math]x_i[/math], вибрано з умови охоплення області їхньої реальної зміни. Рівні змінних становили, %:
| Незалежні змінні | Нижній | Основний | Верхній |
|---|---|---|---|
| [math]X_1[/math] | |||
| [math]X_2[/math] | |||
| [math]X_3[/math] |
У зв'язку з тим, що режими крупоутворення вивчалися досить детально, стало можливим ставити експерименти в області факторного простору, для якої значення всіх у близькі до оптимальних, а для опису цієї області застосувати відразу планування другого порядку. Було реалізовано центральний композиційний рототабельний план, який включає ПФЕ [math]2^3[/math], шість зіркових та шість центральних точок. Послідовність проведення дослідів була рандомізована, кожен дослід проводився тричі. У табл. 4 наведено матрицю планування та середні значення функцій відклику для кожного її рядка.
За вищенаведеними формулами розраховані такі коефіцієнти в рівняннях регресії для всіх функцій відклику:
[math]\begin{align} & {{y}_{1}}=0,65+0,0084{{z}_{1}}+0,0048{{z}_{2}}+0,0630{{z}_{3}}+0,0150{{z}_{1}}{{z}_{2}}-0,0050{{z}_{1}}{{z}_{3}}- \\ & -0,0400{{z}_{2}}{{z}_{3}}+0,0038z_{1}^{2}+0,0076z_{2}^{2}+0,0314z_{3}^{2}; \\ & {{y}_{2}}=43,5+1,37{{z}_{1}}+0,34{{z}_{2}}+0,89{{z}_{3}}-1,41{{z}_{1}}{{z}_{2}}-0,61{{z}_{1}}{{z}_{3}}+ \\ & +0,74{{z}_{2}}{{z}_{3}}-0,83z_{1}^{2}-1,71z_{2}^{2}-1,52z_{3}^{2}; \\ & {{y}_{3}}=6,4-0,28{{z}_{1}}-0,11{{z}_{2}}+0,61{{z}_{3}}+0,03{{z}_{1}}{{z}_{2}}-0,03{{z}_{1}}{{z}_{3}}- \\ & -0,05{{z}_{2}}{{z}_{3}}+0,33z_{1}^{2}+0,68z_{2}^{2}+0,69z_{3}^{2}. \\ \end{align}[/math]
Оцінки дисперсій для коефіцієнтів у цих рівняннях наведено в табл. 5. Коефіцієнти при [math]z^2[/math] на порядок перевищують помилку в їхньому визначенні для всіх функцій відклику, отже, лінійними рівняннями описати їх не можна. Адекватність утворених нелінійних рівнянь було перевірено за F-критерієм.
| [math]z_0[/math] | [math]z_1[/math] | [math]z_2[/math] | [math]z_3[/math] | [math]z_1^2[/math] | [math]z_2^2[/math] | [math]z_3^2[/math] | [math]z_1*z_2[/math] | [math]z_1*z_3[/math] | [math]z_2*z_3[/math] | [math]y_1c[/math] | [math]y_2c[/math] | [math]y_3c[/math] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]{{\operatorname{y}}_{i}}[/math] | [math]{{\operatorname{S}}_{b0}}[/math] | [math]{{\operatorname{S}}_{b1}}[/math] | [math]{{\operatorname{S}}_{b2}}[/math] | [math]{{\operatorname{S}}_{b3}}[/math] |
|---|---|---|---|---|
| [math]y_1[/math] | 0,0053 | 0,0035 | 0,0034 | 0,0046 |
| [math]y_2[/math] | 0,48 | 0,31 | 0,30 | 0,41 |
| [math]y_3[/math] | 0,13 | 0,8 | 0,8 | 0,11 |
Перелік використаних джерел
- http://tstu.edu.ua/(березень2010)
- Аністратенко В.О., Федоров В.Г. Математичне планування експериментів в АПК http://tstu.edu.ua/(березень2010)