Дрейф у плануванні експеременту

Планування експерименту при наявності некерованих змінних

ВСТУП

При утворенні математичних моделей з великим числом змінних треба провести значну кількість дослідів. Кожний окремий дослід проводиться протягом тривалого періоду. У той же час властивості багатьох об’єктів сільськогосподарського та харчового виробництва змінюються в часі. Наприклад, в біотехнології урожай маси змінюється в міру зміни властивостей посівної культури або живильного середовища. У харчових галузях при дослідженні інтенсивності роботи випарних апаратів з плином часу на теплообмінній поверхні відкладається накип , що неминуче веде до поступового зниження функції відклику, оскільки накип збільшує термічний опір теплопередачі. Подібні зміни при змінні якості сировини мають місце для функцій відклику також і в інших галузях. Такі об’єкти називаються дрейфуючими.

Вплив дрейфу на експеримент

Вплив дрейфу на параметри математичного опису процесу можна усунути, застосовуючи спеціальні методи планування. Звичайно припускають, що дрейф не взаємодії з факторами, варіюючи ми в процесі експерименту, тобто виконується умова адитивності дрейфу. Дослідження сільськогосподарських і технологічних процесів з дрейфом характеристик ускладнюється тим, що умова адитивності може бути прийнята далеко не завжди. Так, у розглянутому вище прикладі з накипом, його зростання може впливати не тільки на функцію відклику, а й на параметри, що відіграють роль незалежних змінних , наприклад, на коефіцієнт тепловіддачі при кипінні розчинів. Адитивний дрейф можна розглядати, як зміщення математичної моделі – поверхні відклику без деформації самої поверхні. Для того, щоб виключити вплив дрейфу, треба досить чітко уявити собі його форму. Найчастіше не можна припускати лише той чи інший його характер і критерієм правильності буде лише величина похибки завбачення на основі утвореної моделі. Розрізняють три форми дрейфу:

• 1) ступінчаста,
• 2) лінійна,
• 3) експоненціальна.

Ступінчастий дрейф

Ступінчастим називається такий дрейф, при якому за час проведення деякої групи дослідів вихідна величина залишається незмінною, тобто виконується умова стаціонарності.

Для виключення ступінчастого дрейфу (іноді його називають також блоковим або дискретним) звичайну матрицю ПФЕ розбивають на ортогональні блоки або групи дослідів, у межах яких величина дрейфу дорівнює нулю.

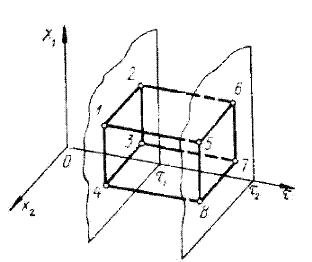
Розбивка на блоки проводиться з урахуванням вимог ортогональності вектор-стовпців матриці планування як між собою, так і до вектора дрейфу, у межах кожного блоку (рис.1).

Рисунок 1. Розбиття на блоки

Тут досліди кожного блоку (1-4, 5-8) розташовуються в площині, перпендикулярній (ортогональній) до осі часу, і, таким чином, дають результати, на яких не відбувається вплив дрейфу.

Розглянемо експеримент в умовах передбачуваного ступінчастого дрейфу з трьома незалежними змінними. Дрейф обумовлено неоднорідністю сировини, величина якої змінюється від партії до партії. Передбачається провести ПФЕ типу 23 з реалізацією перших чотирьох дослідів на одній партії, а решти чотирьох – на іншій. Розбиваємо матрицю планування на два блоки, порівнюючи потрійну взаємодію z1z2z3 новою незалежною змінною zд, що характеризує дрейф, тобто zд= z1z2z3. Для одного з блоків відберемо досліди, для яких zд=+1, і вони будуть проводитися на одній партії сировини, для іншого – досліди, для яких zд=-1 (інша партія сировини). Формально це планування, матрицю якого наведено в таблиці 1, можна розглянути як ДФЕ з генеруючим співвідношенням zд= z1z2z3.

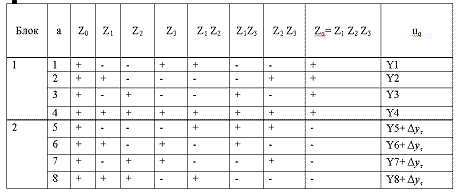
Таблиця 1. матриця планування при ступінчастому дрейфі

Реалізація матриці здійснюється за блоками. Планування в умовах ступінчастого дрейфу дає змогу проводити паралельні експерименти.

Лінійний і експоненціальний дрейф

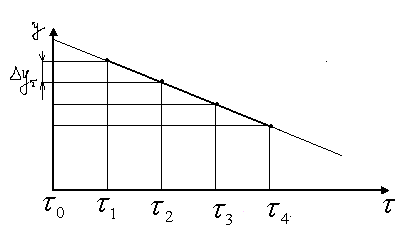
У виробничій практиці та лабораторних дослідженях часто має місце ситуація, коли під дією факторів, які не належать до керованих змінних, вихідна величина у змінює своє значення при переході від досліду до досліду. У випадку, коли відомо тільки те, що вихід падає або зростає і ніяких інших відомостей про характер дрейфу немає, часто нічого не лишається іншого, як вважати його лінійним. Планування експерименту, ортогональне до лінійного дрейфу, проводиться за допомогою матриці планування ПФЕ типу N=22, що вважається можливим, коли при кожному наступному вимірюванні складова лінійного дрейфу змінюється на одну й ту ж величину . Виконання цієї умови не зустрічає особливих ускладнень і досягається експериментуванням через строго визначені, рівні проміжки часу. Тут лінійний дрейф можна подати у вигляді ступінчастої функції з N рівнями.

Список використаних джерел

1. 1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. - Планирование эксперимента при поиске оптимальных условий (1973).
2. 2. Аністратенко В.О., Федоров В.Г. Математичне планування експерименту в АПК. К.: Вища школа, 1993. – 375 с.
3. 3. Конкретні методики викладання. Щетініна О.К., Карпенко О.Н., Донецький національний університет економіки і торгівлі імені Михайла Туган-Барановського

Студент: Користувач:POWER

Виступ відбувся: 4 березня 2010

Тема: планування експерименту при наявності некерованих змінних