Відмінності між версіями «Коефіцієнт Дарсі»
Юлько (обговорення • внесок) |
Юлько (обговорення • внесок) (→Коефіцієнт Дарсі (гідравлічний коефіцієнт тертя).) |
||
| Рядок 6: | Рядок 6: | ||
== Коефіцієнт Дарсі (гідравлічний коефіцієнт тертя).== | == Коефіцієнт Дарсі (гідравлічний коефіцієнт тертя).== | ||
| + | λ - коефіцієнт гідравлічного тертя, безрозмірна величина, що характеризує співвідношення сил тертя і інерції, і саме її визначення і є предмет гідравлічного розрахунку трубопроводу. | ||
| + | Втрати на тертя обумовлені в'язкісні тертям шарів рідини, що рухаються усередині потоку з різною швидкістю, а також тертям об внутрішню поверхню труби шарів рідини, що рухаються в безпосередній близькості від неї. | ||
| + | |||
Для круглих труб сталого перерізу втрати напору на тертя визначають за формулою Дарсі: | Для круглих труб сталого перерізу втрати напору на тертя визначають за формулою Дарсі: | ||
Версія за 20:54, 23 червня 2011
Анрі Філібер Гаспар Дарсі (10 червня 1803, Діжон, - 2 січня 1858, Париж) - французький інженер-гідравлік, котрий обгрунтував закон Дарсі (1856), що зв'язує швидкість фільтрації рідини в пористому середовищі з градієнтом тиску: «Очевидно, для піску однієї якості витрата, що пропускається ним прямо пропорційна натиску і обернено пропорційна товщині фільтруючого шару (ґрунту)».
Під керівництвом Дарсі в м. Діжоні була створена перша в Європі система міських очисних споруд з різними фільтраційними засипками. Ім'ям Дарсі названа одиниця вимірювання проникності пористого середовища.
Зміст
Коефіцієнт Дарсі (гідравлічний коефіцієнт тертя).
λ - коефіцієнт гідравлічного тертя, безрозмірна величина, що характеризує співвідношення сил тертя і інерції, і саме її визначення і є предмет гідравлічного розрахунку трубопроводу. Втрати на тертя обумовлені в'язкісні тертям шарів рідини, що рухаються усередині потоку з різною швидкістю, а також тертям об внутрішню поверхню труби шарів рідини, що рухаються в безпосередній близькості від неї.
Для круглих труб сталого перерізу втрати напору на тертя визначають за формулою Дарсі:
[math]\mathcal{E}=\text{ }\!\!\lambda\!\!\text{ *}\frac{\text{L}}{\text{D}}[/math]
де λ — гідравлічний коефіцієнт тертя по довжині.
Тоді формула Дарсі набуває вигляду:
[math]\text{ }\!\!\Delta\!\!\text{ h=}\lambda *\frac{\text{L}}{\text{D}}*\frac{{{\text{V}}^{2}}}{2\text{g}}[/math]
де L і D — відповідно довжина та діаметр трубопроводу; V — середня швидкість руху рідини; λ — коефіцієнт гідравлічного тертя, який залежить від в'язкості, яка входить до числа Рейнольдса та відносної шорсткості стінок труби .
або для втрати тиску:
[math]\text{ }\!\!\Delta\!\!\text{ p=}\lambda *\frac{\text{L}}{\text{D}}*\frac{{{\text{V}}^{2}}}{2}*\rho[/math]
Якщо визначаються втрати на тертя для труби не круглого поперечного перерізу, то за D береться гідравлічний діаметр.
Слід відзначити, що втрати напору на гідравлічних опорах не завжди пропорційні швидкісному напору.
Визначення гідравлічного коефіцієнта тертя по довжині
Експериментально встановлено,що гідравлічний коефіцієнт тертя,як правило залежить від режиму руху рідини,який характеризується числом Рейнольдса(Re)і внутрішньої поверхні трубопроводу,який характеризується відносною шорсткістю (ε).Вплив цих факторів на величину λ при ламінарному і турбулентному режимах проявляється по-різному.
При ламінарному режимі: [math]\operatorname{Re}=\frac{\vartheta \cdot d}{\nu }\,\le \,2300[/math] (ν Кінематична в'язкість)стан поверхності стінки не впливає на опір рідини і λ= f(Re).Значення коефіцієнта λ в цьому випадку визначається за формулою :
[math]\lambda \text{=}\frac{64}{\operatorname{Re}}[/math]
де Re — число Рейнольдса.
Іноді для гнучких труб у розрахунках приймають
[math]\lambda \text{=}\frac{68}{\operatorname{Re}}[/math]
Турбулентний режим течії характеризується інтенсивним перемішуванням рідини як у поперечному (по перерізу потоку), так і в поздовжньому (по довжині потоку) напрямках.Проте в діапазоні чисел Рейнольдса [math]2320\,\le \,\operatorname{Re}\,\le \,{{10}^{5}}[/math] безпосередньо поблизу стінок трубопроводу існує шар рухомої рідини, перебіг в якому зберігається ламінарним.
Для турбулентної течії існують складніші залежності. Одна з найпоширеніших формул — це формула Блазіуса:
[math]\lambda \text{=}\frac{0,316}{^{4}\sqrt{\operatorname{Re}}}[/math]
Визначення коефіцієнта Дарсі для місцевих опорів .
Для кожного виду місцевих опорів існують свої залежності для визначення коефіцієнта ξ. До числа найбільш поширених місцевих опорів відносяться раптове розширення труби, раптове звуження труби і поворот труби.
1. При раптовому розширенні труби:
[math]\varepsilon \text{=(1-}\frac{{{S}_{1}}}{{{S}_{2}}}{{\text{)}}^{2}}[/math]
де S1 і S2 - площі поперечного перерізу труби, відповідно перед розширенням і після нього.
2. При раптовому звуженні труби коефіцієнт Дарсі визначається за формулою:
[math]\varepsilon \text{=(}\frac{1-{{S}_{2}}/{{S}_{1}}}{2}\text{)}[/math]
де S1 і S2 - площі поперечного перерізу труби, відповідно, перед звуженням і після нього.
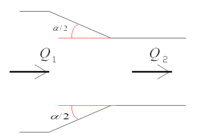
3. При поступовому звуженні труби (конфузор):
[math]\varepsilon \text{=}\frac{{{\lambda }_{}}}{8\sin \text{ }\!\!\alpha\!\!\text{ /2 }}*(1-\frac{1}{{{n}^{2}}})[/math]
де -
[math]n\text{=}\frac{{{S}_{1}}}{{{S}_{2}}}[/math] ступінь звуження; λ - коефіцієнт втрат на тертя по довжині при турбулентному режимі.
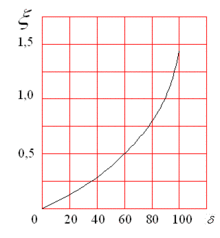
4. При різкому (без закруглення) повороті труби (коліно) коефіцієнт Дарсі визначається за графічним залежностям (рис. 2).
Література
Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с.
О.М. Коваленко,Т.О. Шевченко Інженерна гідравліка. Розділ I. Рух рідини в закритих руслах – Харків: ХНАМГ, 2007.-76 с
Идельчик И.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559 с.
Дробинс В. Ф. Гидравлика и гидравлические машины. – М.: Просвещение, 1982.
Установка для изучения потерь напора при турбулентном установившемся движении (тип ГВ5). – Одесоргнаучкомплектснаб. – 39 с.