Відмінності між версіями «Кінематика рідин»
| Рядок 81: | Рядок 81: | ||
| − | <math>Q=\int{\int\limits_{S}{C\cdot \cos (\overset{\wedge }{\mathop{nC}}\,}})\cdot d\omega </math або | + | |
| + | <math>Q=\int{\int\limits_{S}{C\cdot \cos (\overset{\wedge }{\mathop{nC}}\,}})\cdot d\omega </math> або | ||
Версія за 20:57, 14 червня 2011
Методи вивчення руху рідини
Кінематика рідини – розділ гідрогазодинаміки, в якому вивчаються лише геометричні властивості руху рідини. В силу цього всі основні виводи кінематики справедливі для любої рідини, як в’язкої, та і нев’язкої. В основу вивчення кінематики рідини покладені гіпотези про неперервність зміни кінематичних параметрів (швидкостей, прискорень). Тобто швидкість рідини передбачається неперервною функцією від координат, а отже такою, яку можна диференціювати. Для зручності досліджень любий рідинний об’єм представляють складеним із великої кількості рідинних частинок. У відповідності до цього до дослідження руху рідинної частинки можливий такий же підхід, як і до досліджень руху точки в механіці. Існують два основних метода дослідження кінематики рідини: метод Лагранжа і метод Ейлера. Переважне розповсюдження одержав метод Ейлера, згідно якого розглядається поле швидкостей в точках простору, занятого рідиною, що рухається. Поле швидкостей задається у вигляді
[math]u={{f}_{1}}(x,y,z,\tau );v={{f}_{2}}(x,y,z,\tau );w={{f}_{3}}(x,y,z,\tau );[/math]
(1.0)
де ,u, v, w– проекції швидкості на декартові вісі координат;
x, у, z – координати точок простору;
[math]\tau[/math]- час
Залежності (1.1) описують неусталений рух, якщо [math]v={{f}_{2}}(x,y,z,\tau );w={{f}_{3}}(x,y,z,\tau );[/math]то рух усталений стаціонарний. Важливі в кінематиці поняття про лінії струменя і траєкторії частинок рідини, що рухаються. Лініями току називають криві, в кожній точці котрих в даний момент часу вектор швидкості співпадає по направленню з дотичною. Диференціальні рівняння ліній струменя мають вигляд
[math]\frac{dx}{u}=\frac{dy}{v}=\frac{dz}{w}[/math](1.2)
а рівняння траєкторії –
[math]\frac{dx}{u}=\frac{dy}{v}=\frac{dz}{w}=d\tau[/math](1.3)
Під траєкторією розуміють геометричне місце послідовних положень частинки, що рухається, в розглядаємій системі координат. При усталеному русі траєкторії і лінії току співпадають. Вектор швидкості частинки рідини можна представити
[math]\overline{C}=\overline{i}\cdot u+\overline{j}\cdot v+\overline{k}\cdot w[/math]
де [math]\overline{i},\overline{j},\overline{k}[/math]- базові вектори
Проекції прискорень рідинної частинки на декартові вісі координат визначають із співвідношень
[math]\begin{align}
& \frac{du}{d\tau }=\frac{\partial u}{\partial \tau }+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial u}+w\frac{\partial u}{\partial z} \\
& \frac{dv}{d\tau }=\frac{\partial v}{\partial \tau }+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z} \\
& \frac{dw}{d\tau }=\frac{\partial w}{\partial \tau }+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z} \\
\end{align}[/math](1.4)
Перші члени правих частин системи рівнянь (1.4) відбивають зміну проекцій швидкостей в даній точці простору в зв’язку зі нестаціонарністю поля швидкості і носять назву локальних прискорень, інші члени зв’язані з неоднорідністю поля швидкостей і називають конвективними прискореннями.
Закон збереження маси
В гідродинаміці цей закон в загальному випадку представляється у вигляді рівняння нерозривності (суцільності)
[math]\frac{\partial \rho }{\partial \tau }+div(\rho \cdot \overline{C)}=0[/math](2.1)
де r – густина рідини. Для нестисливої рідини
[math]div(\rho \cdot \overline{C)}=0[/math] (2.2)
або в проекції на декартові вісі координат
[math]\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0[/math](2.3)
Рух нестисливого суцільного середовища можливий лише у випадку, коли для розглядаємого поля швидкостей справедлива рівність (2.3) Потік вектора швидкості через поверхню w є скалярною величиною, яка визначається за формулою
[math]Q=\int{\int\limits_{S}{\overline{C}\cdot }}\overline{n}\cdot d\omega[/math] (2.4)
де [math]n[/math]-нормальдо поверхні
[math]Q=\int{\int\limits_{S}{C\cdot \cos (\overset{\wedge }{\mathop{nC}}\,}})\cdot d\omega[/math] або
В координатній формі
[math]Q=\int{\int\limits_{S}{(u\cdot {{n}_{x}}+v\cdot {{n}_{y}}+w\cdot {{n}_{z}}}}\cdot d\omega[/math](2.5)
Фізично потік вектора швидкості уявляє собою секундну об’ємну витрату рідини через поверхню w. Сукупність ліній течії, які проходять через всі точки нескінченно малого замкнутого контуру, утворюють поверхню, яка називається трубкою течії. Рідина, яка заключна в середині трубки току, називається струменем. Рівняння суцільності для струменя нестисливої рідини має вигляд
де dQ – елементарна об’ємна витрата через поперечний переріз струменя;
Із рівняння (2.5) витікає, що елементарна об’ємна витрата стала вздовж струменя. Для потоку кінцевих розмірів рівняння нерозривності має вигляд
де V – середня швидкість в розглядаємому перерізі; w – площа поперечного перерізу потоку.
Одновимірна течія рідини
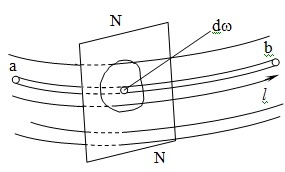
Рис. 3.1. Рух потоку рідини
Широке коло питань технічної механіки рідини може бути вирішене за допомогою специфічного підходу до вивчення руху рідини, котрий називається методом гідравліки. Його сутність полягає в наступному.
Течію рідини подумки розбивають на ряд елементарних струминок (рис. 3.1), щоб вісь кожної з них була дотична до напрямку швидкості. Потім дійсну течію з різними швидкостями окремих струминок заміняють розрахунковою моделлю потоку, котрий рухається як одне суцільне ціле з сталою для всіх частинок в даному перерізі швидкістю.
При такій схематизації течії швидкості і прискорення в напряму, нормальному до основного руху, не враховуються.
Для опису такої течії достатньо тільки однієї координати простору – відстані l вздовж вісі потоку від перерізу, що розглядається, відносно деякої початкової точки О. Тому такий рух і називають одновимірним. Розв’язування задач одновимірної течії рідини є предметом гідравліки.
Живим перерізом називається площа поперечного перерізу потоку, яка нормальна до напрямку течії.
Витратою потоку