Відмінності між версіями «Лінія течії»
SashOK (обговорення • внесок) |
SashOK (обговорення • внесок) |
||
| Рядок 1: | Рядок 1: | ||
| − | '''Лінії течії''' – лінії, дотичні до яких у кожній точці співпадають за напрямом з векторами швидкостей частинок рідини, а густина проведення ліній течії (відношення числа ліній <math>\triangle\</math>N до величини перпендикулярної до них площі <math>\triangle\</math>S, через яку вони проходять) пропорційна величині швидкості у даній точці. | + | '''Лінії течії''' – лінії, дотичні до яких у кожній точці співпадають за напрямом з векторами швидкостей частинок рідини, а густина проведення ліній течії (відношення числа ліній <math>\triangle\</math>N до величини перпендикулярної до них площі <math>\triangle\</math>S, через яку вони проходять) пропорційна величині швидкості у даній точці. Сукупність ліній течії називають ''спектром течії''. Спектри дають змогу розглядати різноманітні гідравлічні явища з якісного боку. |
| + | |||
| + | == Пояснення принципу == | ||
| − | |||
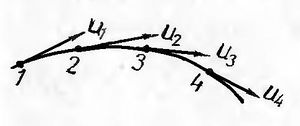
Наочне уявлення про миттєву картину течії рідини дають так звані лінії течії. Щоб усвідомити зміст поняття лінії течії, уявимо собі, що в рідині, яка перебуває в русі, проведено певну криву, дотичні до якої у довільній точці в дану мить часу збігаються з напрямом вектора швидкості. Тоді така крива, яку називатимемо ''лінією течії'', дає змогу визначити напрямок миттєвих швидкостей в усіх точках цієї кривої. [[Файл:Liniya techii.jpg|right|thumb]] | Наочне уявлення про миттєву картину течії рідини дають так звані лінії течії. Щоб усвідомити зміст поняття лінії течії, уявимо собі, що в рідині, яка перебуває в русі, проведено певну криву, дотичні до якої у довільній точці в дану мить часу збігаються з напрямом вектора швидкості. Тоді така крива, яку називатимемо ''лінією течії'', дає змогу визначити напрямок миттєвих швидкостей в усіх точках цієї кривої. [[Файл:Liniya techii.jpg|right|thumb]] | ||
Лінії течії як на поверхні, так і всередині рухомої рідини легко зробити видимими, якщо ввести в рідину різні нерозчинні речовини, які можуть рухатися разом з рідиною. Вигляд ліній течії змінюється зі зміною розподілу швидкостей. В умовах стаціонарного руху лінії течії не змінюють свого обрису в потоці, отже вони збігаються з траєкторіями. При нестаціонарному русі дотичними по лінії течії є швидкості різних частинок, тому в цьому випадку лінії і траєкторії не суміщаються. | Лінії течії як на поверхні, так і всередині рухомої рідини легко зробити видимими, якщо ввести в рідину різні нерозчинні речовини, які можуть рухатися разом з рідиною. Вигляд ліній течії змінюється зі зміною розподілу швидкостей. В умовах стаціонарного руху лінії течії не змінюють свого обрису в потоці, отже вони збігаються з траєкторіями. При нестаціонарному русі дотичними по лінії течії є швидкості різних частинок, тому в цьому випадку лінії і траєкторії не суміщаються. | ||
| − | + | == Розрахунок лінї течії == | |
Можна сказати, що лінії течії аналогічні силовим лініям силових полів. | Можна сказати, що лінії течії аналогічні силовим лініям силових полів. | ||
| Рядок 26: | Рядок 27: | ||
Рівняння (1.2) є рівнянням лінії течії плоского потоку. | Рівняння (1.2) є рівнянням лінії течії плоского потоку. | ||
| + | |||
| + | == Струминна модель потоку == | ||
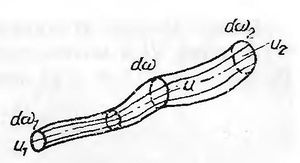
Уявимо собі тепер, що в рухомій рідині виділено замкнений контур з елементакрною площею поперечного перерізу <math>dw</math>. [[Файл:trubka techii.jpg|right|thumb]] | Уявимо собі тепер, що в рухомій рідині виділено замкнений контур з елементакрною площею поперечного перерізу <math>dw</math>. [[Файл:trubka techii.jpg|right|thumb]] | ||
| Рядок 31: | Рядок 34: | ||
Поверхню, утворену лініями течії, проведеними через усі точки цього замкненого контуру, називають трубкою течії, а масу рідини що протікає всередині трубки течії, - елементарною струминкою. Струминна модель потоку введена Л.Ейлером. | Поверхню, утворену лініями течії, проведеними через усі точки цього замкненого контуру, називають трубкою течії, а масу рідини що протікає всередині трубки течії, - елементарною струминкою. Струминна модель потоку введена Л.Ейлером. | ||
| − | Слід підкреслити, що при стаціонарному русі трубка течії, утворена лініями течії, не змінюється в часі та є немовби непроникною трубкою, в якій рідина тече як в трубці з твердими стінками що обмежують її вміст. Рідина з трубки течії не витікає в сторону і не додається до неї, тому що у всіх точках струминки швидкість спрямована вздовж лінії течії. | + | Слід підкреслити, що при стаціонарному русі трубка течії, утворена лініями течії, не змінюється в часі та є немовби непроникною трубкою, в якій рідина тече як в трубці з твердими стінками що обмежують її вміст. Рідина з трубки течії не витікає в сторону і не додається до неї, тому що у всіх точках струминки швидкість спрямована вздовж лінії течії.В елементарній струминці швидкості в усіх точках одного й того ж поперечного перерізу можна приймати однаковими і рівними місцевими швидкостями. |
| − | + | == Висновки == | |
| − | Відповідно до цієї моделі, введеної в гідравліку ще в період формування її як науки, простір, зайнятий рухомою рідиною, умовно розглядають як сукупність цілого ряду елементарних струминок, що протікають через достатньо велику площу, утворює ''потік рідини''. | + | Елементарна струминка є наочним кінематичним образом, який істотно полегшує вивчення руху рідини і покладений в основу так званої ''струминної моделі'' руху рідини. Відповідно до цієї моделі, введеної в гідравліку ще в період формування її як науки, простір, зайнятий рухомою рідиною, умовно розглядають як сукупність цілого ряду елементарних струминок, що протікають через достатньо велику площу, утворює ''потік рідини''. |
Струминна модель течії сьогодні є однією з основних моделей потоку рідини. | Струминна модель течії сьогодні є однією з основних моделей потоку рідини. | ||
| + | |||
| + | == Перелік посилань == | ||
| + | |||
| + | Левицкий Б. Ф., Лещій Н. П. Гідравліка. Загальний курс : підручник / Б. Ф. Левицький., Лещій Н. П. – Львів : Світ, 1994. – 264 с. | ||
Версія за 16:01, 8 червня 2011
Лінії течії – лінії, дотичні до яких у кожній точці співпадають за напрямом з векторами швидкостей частинок рідини, а густина проведення ліній течії (відношення числа ліній [math]\triangle\[/math]N до величини перпендикулярної до них площі [math]\triangle\[/math]S, через яку вони проходять) пропорційна величині швидкості у даній точці. Сукупність ліній течії називають спектром течії. Спектри дають змогу розглядати різноманітні гідравлічні явища з якісного боку.
Зміст
Пояснення принципу
Наочне уявлення про миттєву картину течії рідини дають так звані лінії течії. Щоб усвідомити зміст поняття лінії течії, уявимо собі, що в рідині, яка перебуває в русі, проведено певну криву, дотичні до якої у довільній точці в дану мить часу збігаються з напрямом вектора швидкості. Тоді така крива, яку називатимемо лінією течії, дає змогу визначити напрямок миттєвих швидкостей в усіх точках цієї кривої.Лінії течії як на поверхні, так і всередині рухомої рідини легко зробити видимими, якщо ввести в рідину різні нерозчинні речовини, які можуть рухатися разом з рідиною. Вигляд ліній течії змінюється зі зміною розподілу швидкостей. В умовах стаціонарного руху лінії течії не змінюють свого обрису в потоці, отже вони збігаються з траєкторіями. При нестаціонарному русі дотичними по лінії течії є швидкості різних частинок, тому в цьому випадку лінії і траєкторії не суміщаються.
Розрахунок лінї течії
Можна сказати, що лінії течії аналогічні силовим лініям силових полів. Якщо за час dt частинка рідини пройде за напрямком лінії течії шлях dl з компонентами на координатних осях, рівним dx, dy, dz, то складові цієї швидкості становитимуть:
[math]u_x=dx/dt; u_y=dy/dt; u_z=dz/dt.[/math]
а тому
[math]dx/u_x=dy/u_y=dz/u_z.[/math] (1.1)
Система рівнянь (1.1) є рівнянням лінії течії. Для плоского руху відповідно можна записати
[math]dx/u_x=dy/u_y=dt[/math]
або
[math]dx/f_1(x,y,t)=dy/f_2(x,y,t)[/math] (1.2)
Рівняння (1.2) є рівнянням лінії течії плоского потоку.
Струминна модель потоку
Уявимо собі тепер, що в рухомій рідині виділено замкнений контур з елементакрною площею поперечного перерізу [math]dw[/math].Поверхню, утворену лініями течії, проведеними через усі точки цього замкненого контуру, називають трубкою течії, а масу рідини що протікає всередині трубки течії, - елементарною струминкою. Струминна модель потоку введена Л.Ейлером.
Слід підкреслити, що при стаціонарному русі трубка течії, утворена лініями течії, не змінюється в часі та є немовби непроникною трубкою, в якій рідина тече як в трубці з твердими стінками що обмежують її вміст. Рідина з трубки течії не витікає в сторону і не додається до неї, тому що у всіх точках струминки швидкість спрямована вздовж лінії течії.В елементарній струминці швидкості в усіх точках одного й того ж поперечного перерізу можна приймати однаковими і рівними місцевими швидкостями.
Висновки
Елементарна струминка є наочним кінематичним образом, який істотно полегшує вивчення руху рідини і покладений в основу так званої струминної моделі руху рідини. Відповідно до цієї моделі, введеної в гідравліку ще в період формування її як науки, простір, зайнятий рухомою рідиною, умовно розглядають як сукупність цілого ряду елементарних струминок, що протікають через достатньо велику площу, утворює потік рідини.
Струминна модель течії сьогодні є однією з основних моделей потоку рідини.
Перелік посилань
Левицкий Б. Ф., Лещій Н. П. Гідравліка. Загальний курс : підручник / Б. Ф. Левицький., Лещій Н. П. – Львів : Світ, 1994. – 264 с.