Відмінності між версіями «Витікання газів через отвори»
Nike (обговорення • внесок) (→Витікання газів через отвори) |
Nike (обговорення • внесок) (→Приклад витікання газу через отвір) |
||
| Рядок 83: | Рядок 83: | ||
<math>{{V}_{1}}>{{a}_{1}}>0</math> (<math>{{a}_{1}}</math> - місцева швидкість звуку). | <math>{{V}_{1}}>{{a}_{1}}>0</math> (<math>{{a}_{1}}</math> - місцева швидкість звуку). | ||
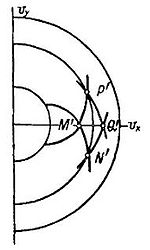
| − | Побудувавши точку <math>{{M}'}</math> (<math>{{V}_{1}}</math>,<math>0</math>)в площині (<math>{{V}_{x}}</math>, <math>{{V}_{y}}</math>)(''рис. 2''), проведемо через <math>A</math> характеристику першого сімейства в площині <math>(x,y)</math>, а через точку <math>B</math> - характеристику другого сімейства (рис. 1). В куті <math>BCA</math> маємо, як і ранше, потік з <math>{{V}_{x}}={{V}_{1}}</math>, <math>{{V}_{y}}=0</math>. Нехай тиск в просторі, в який виходить газ, буде <math>{{\rho }_{2}}</math>. Побудуємо в площині (<math>{{V}_{x}}</math>, <math>{{V}_{y}}</math>) круг радіуса <math>{{V}_{2}}</math>, який визначаємо з рівняння ''Бернуллі'' при <math>p={{\rho }_{2}}</math>. Рухаючись по епіціклоіду першого сімейства, який проходить через <math>{{M}'}</math>, знайдемо швидкість <math>{{P}'}</math> біля точки <math>B</math> (взагалі ми, очевидно, будемо мати симетрію по відношення до осі отвору). Знаючи <math>{{N}'}</math> і <math>{{P}'}</math>, проведемо характеристики '''AD''' і '''BE''' і заповнимо кути <math>\text{CAD}</math> і <math>\text{CBE}</math> пучками характеристик. | + | Побудувавши точку <math>{{M}'}</math> (<math>{{V}_{1}}</math>,<math>0</math>)в площині (<math>{{V}_{x}}</math>, <math>{{V}_{y}}</math>) (''рис. 2''), проведемо через <math>A</math> характеристику першого сімейства в площині <math>(x,y)</math>, а через точку <math>B</math> - характеристику другого сімейства (''рис. 1''). В куті <math>BCA</math> маємо, як і ранше, потік з <math>{{V}_{x}}={{V}_{1}}</math>, <math>{{V}_{y}}=0</math>. Нехай тиск в просторі, в який виходить газ, буде <math>{{\rho }_{2}}</math>. Побудуємо в площині (<math>{{V}_{x}}</math>, <math>{{V}_{y}}</math>) круг радіуса <math>{{V}_{2}}</math>, який визначаємо з рівняння ''Бернуллі'' при <math>p={{\rho }_{2}}</math>. Рухаючись по епіціклоіду першого сімейства, який проходить через <math>{{M}'}</math>, знайдемо швидкість <math>{{P}'}</math> біля точки <math>B</math> (взагалі ми, очевидно, будемо мати симетрію по відношення до осі отвору). Знаючи <math>{{N}'}</math> і <math>{{P}'}</math>, проведемо характеристики '''AD''' і '''BE''' і заповнимо кути <math>\text{CAD}</math> і <math>\text{CBE}</math> пучками характеристик. |
Версія за 17:18, 7 червня 2011
Зміст
Витікання
Витікання - якщо два матеріальних середовища відокремлені один від одного стінкою, яка має отвори, і тиск, під яким знаходяться ці середовища, неоднакові, то середовище, що знаходиться під великим тиском, виходить в сусіднє середовище у вигляді струменя - потоку першого середовища, обмеженого з усіх сторін другим середовищем. Це явище називається витіканням. Витікання відбувається або під впливом зовнішніх сил, або під впливом сили тяжіння, або, нарешті, під сукупною їх дією. Від витікання потрібно відрізняти вихід одного середовища в інше, що знаходиться під тим же тиском, під впливом одних внутрішніх (молекулярних сил); Це явище є дифузією. Витікання тіл можна спостерігати при всіх трьох станах – твердому, рідкому і газоподібному.
Легше і найчастіше спостерігається витікання рідин, і тому витікання вивчено майже виключно на рідинах; знайдені закони з успіхом були застосовані згодом до твердих тіл і газів. Теорія витікання становить одну з важливих розділів гідродинаміки – вчення про рух рідини; практична її сторона і додатки розглядаються в гідравліці або гідротехніці.
Витікання газів через отвори
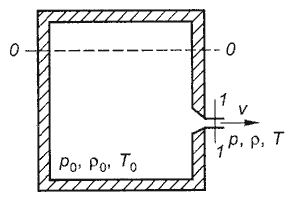
Витікання газів через отвори слідує тим же основним законам, що і витікання рідин; але у випадку газів ми маємо діло з речовиною, обсяг і щільність якої залежить від тиску, тому не можна, як у випадку рідин, вважати середовище нестискуваним. Витікання завжди відбувається під впливом різниці тиску, а отже, витікаючий струмінь газу, що потрапляє в середовище з меншим тиском, займає більший об'єм, розширюється. Розширення газу завжди супроводжується охолодженням його, а охолодження в свою чергу ж кличе за собою знову зміни в об’ємі, щільності і тиску. Зважаючи на це, розвязування загальних задач про витікання газів представляє одну з найважчих розділів аеродинаміки - науки про рухи газів; повний розгляд питань витікання газів мало б вестися не тільки на підставі принципів гідродинаміки, але і на підставі механічної теорії тепла і кінетичної теорії газів. Якщо знехтувати охолодженням газу від розширення і дією сили тяжіння, то для швидкості V витікання газу, під впливом однієї різниці тиску, отримаємо формулу:
[math]V={{a}^{2}}\frac{2\ln \frac{{{\rho }_{0}}}{{{\rho }_{1}}}}{1-{{(\frac{{{q}_{1}}{{\omega }_{1}}}{{{q}_{0}}{{\omega }_{0}}})}^{2}}}[/math] (1)
де [math]a[/math] - стала Маріотта; [math]{{\rho }_{0}}[/math], [math]{{q}_{0}}[/math], [math]{{\omega }_{0}}[/math] - тиск, перетин і щільність для посудини, з якої закінчується газ; [math]{{\rho }_{1}}[/math], [math]{{q}_{1}}[/math], [math]{{\omega }_{1}}[/math] - ті ж величини для місця найменшого перерізу струменя.
Більш простий вираз для [math]V[/math] отримаємо з формули Торрічеллі, застосувавши її до газів:
[math]V=\sqrt{\frac{2g({{\rho }_{0}}-{{\rho }_{1}})}{\omega }}[/math] (2)
Якщо візьмемо, що газ виходить під тиском однієї атмосфери з отвору в порожнечу, то отримаємо за цією формулою для повітря, що виходить в порожнечу, величезну швидкість в 396 метрів, що дорівнює швидкості рушничної кулі; для водню - швидкість в 4 рази більшу і т.д.
З формули (2) випливає, що швидкості витікання газів обернено пропорційні їх плотностям (див. Дифузія). Цей закон, знайдений дослідно Гремом (1836) і підтверджений точними дослідами Бунзена (1857), служить підставою для одного із способів визначення щільності газів.
При вітіканні газів у вигляді струменя спостерігається те ж основне явище стиснення струменя, що і при витіканні рідин. Його легко помітити, якщо спостерігати витікання струменя пофарбованого газу або тютюнового диму. Чудово, що коефіцієнт стиснення струменя [math](K)[/math] для газів дуже близький за величиною до того ж коефіцієнту для рідин. Так, за Вейсбаха, величини [math]K[/math]:
Отвір з досконалою насадкою - 0,947
Отвір з конічною - 0,883
Отвір з циліндричною - 0,839
Отвір з в тонкій стінці - 0,671
На цей коефіцієнт необхідно помножити перетин отвору при визначенні кількості газу який витік в одиницю часу. Питання про величину тиску в місці звуження, тобто про величину [math]{{\rho }_{1}}[/math] формула (1), вирішив приблизно Гюгоніо (1886), який показав, що [math]{{\rho }_{1}}[/math] дорівнює тиску [math]{{\rho }_{2}}[/math] в тому середовищі, в яку газ витікає, лише тоді, коли при повільному витіканні [math]{{\rho }_{2}}\gt 0.607{{\rho }_{0}}[/math], а при бистрому [math]{{\rho }_{2}}\gt 0.522{{\rho }_{0}}[/math]; якщо ж [math]{{\rho }_{2}}\lt \beta {{\rho }_{0}}[/math](де [math]\beta[/math] рівно 0,607 або 0,522), то [math]{{\rho }_{1}}=\beta {{\rho }_{0}}[/math]. Звідси випливає чудове, спостережене ще Вейсбахом (1855), Гирном (1885) та іншими, але пояснене лише Гюгоніо явище, а саме, що кількість витікаючого в одиницю часу газу зростає пропорційно різниці тиску лише до тих пір, поки відношення тисків у двох середовищах не досягне 0,5-0,6; вище того швидкість витікання газу постійна. Це цілком підтвердилося новітніми дослідами Сальхера і Вейсхіда (1889).
Витікання по трубах
При течії по трубах закони витікання для газів ті ж, що і для рідин; швидкість витікання сповільнюється і виражається вже формулою:
[math]V=\sqrt{2g\frac{({{\rho }_{0}}-{{\rho }_{1}})}{\omega }}\frac{d}{d+\varepsilon l}[/math] (3)
де [math]d[/math] - діаметр трубки; [math]l[/math] - довжина трубки; [math]\varepsilon[/math] - величина, що характеризує тертя повітря об стінки трубки.
За Вейсбаха, для скла рівно 0,02197, а по Д'Обюісону для металевих труб - 0,0238. Цей останній вчений знайшов з цілого ряду дослідів емпіричну формулу, яка показує досить точну кількість газу що випливає по трубі в одиницю часу, а саме:
[math]M=2279\sqrt{\frac{\rho {{d}^{5}}}{l+47d}}[/math] (4)
де [math]\rho[/math] виражено у тиску ртутного стовпчика.
Витікання з волосних трубок
При витіканні газів з волосних трубок вони відповідають, як і рідини, закону Пуазейля. Витіканням газів з волосних трубок користуються для визначення внутрішнього їх тертя. При витіканні гази утворюють струмені, що представляють всі особливості рідких струменів - реакцію (ракети, віддача від пострілів), удар струменя і т. д. (див. Струмінь). При дії миттєвих сил витікання газів відбувається у вигляді вихору (при вибухах, при утворенні фосфористого водню і т. д.).
Теорія витікання газів дуже важлива для техніки - газопровідної справи, пристроїв пневматичної передачі, повітродувних приладів, вентиляційних і димових труб; в науці вона важлива для теоретичної метеорології (вітри). Значні математичні труднощі уповільнюють поки повну розробку питань про витікання газів і парів.
Приклад витікання газу через отвір
Розглянемо приклад витікання газу через отвір.
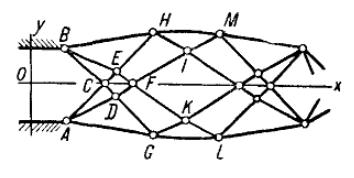
Нехай газ виривається через отвір (дві паралельні прямі), причому швидкість руху біля місця виходу AB (рис. 1) має компоненти:
[math]{{V}_{x}}={{V}_{1}}[/math]; [math]{{V}_{y}}=0[/math];
[math]{{V}_{1}}\gt {{a}_{1}}\gt 0[/math] ([math]{{a}_{1}}[/math] - місцева швидкість звуку). Побудувавши точку [math]{{M}'}[/math] ([math]{{V}_{1}}[/math],[math]0[/math])в площині ([math]{{V}_{x}}[/math], [math]{{V}_{y}}[/math]) (рис. 2), проведемо через [math]A[/math] характеристику першого сімейства в площині [math](x,y)[/math], а через точку [math]B[/math] - характеристику другого сімейства (рис. 1). В куті [math]BCA[/math] маємо, як і ранше, потік з [math]{{V}_{x}}={{V}_{1}}[/math], [math]{{V}_{y}}=0[/math]. Нехай тиск в просторі, в який виходить газ, буде [math]{{\rho }_{2}}[/math]. Побудуємо в площині ([math]{{V}_{x}}[/math], [math]{{V}_{y}}[/math]) круг радіуса [math]{{V}_{2}}[/math], який визначаємо з рівняння Бернуллі при [math]p={{\rho }_{2}}[/math]. Рухаючись по епіціклоіду першого сімейства, який проходить через [math]{{M}'}[/math], знайдемо швидкість [math]{{P}'}[/math] біля точки [math]B[/math] (взагалі ми, очевидно, будемо мати симетрію по відношення до осі отвору). Знаючи [math]{{N}'}[/math] і [math]{{P}'}[/math], проведемо характеристики AD і BE і заповнимо кути [math]\text{CAD}[/math] і [math]\text{CBE}[/math] пучками характеристик.
Нехай [math]\text{CD}[/math] і [math]\text{CE}[/math] будуть криволінійні відрізки характеристик другого і першого сімейства відповідно, що виходять із [math]\text{C}[/math]. Із розгляду руху в кутах ми будемо знати ці лінії, а також будемо знати швидкість вздовж них. Тепер ми найдем рух в криволінійному чотирикутнику [math]\text{ECDF}[/math] [точці [math]\text{F}[/math] відповідає точка [math]{{Q}'}[/math] площини [math]({{V}_{x}},{{V}_{y}})[/math]] (рис. 2). Знаходимо рух в області [math]\text{ADG}[/math] (і [math]\text{BEH}[/math]), де [math]\text{DG[/math] (i [math]\text{EH}[/math]) - – характеристика другого (першого) сімейства, проведена через [math]\text{D}[/math] ([math]\text{E}[/math]), причому попутно ми зможемо знайти форму вільної поверхності [math]\text{AG}[/math] [math]{{(BH)}^{1}})[/math]. Визначивши швидкості на [math]DG[/math] і [math]DF[/math] ([math]EH[/math] i [math]EF[/math]), можемо знайти рух в чотирикутнику [math]\text{DGKF}[/math] ([math]\text{FEHI}[/math]), де [math]\text{FK}[/math] ([math]\text{FI}[/math]) - – характеристика другого (першого) сімейства, яка виходить із [math]\text{F}[/math], а [math]\text{GK}[/math] ([math]\text{HI}[/math]) - характеристика першого (другого) сімейства, яка іде із [math]\text{G}[/math] ([math]\text{H}[/math]). Потім ми рішаємо задачу для області [math]\text{GKL}[/math] ([math]\text{HIM}[/math]), причому попутно визначаємо і вільну поверхню (на цей раз криволінійну) і т.д. В підсумку ми получаємо картину періодичного звуження і розширення струменя, причому максимальна швидкість досягається всередині струменя.
Література
- Юренев В.Н.. Теплотехнический справочник (Том 2);
- Кочин Н.Е., Кибель И.А., Розе Н.В. - Теоретическая гидромеханика (в 2-х частях) - 1963;
- Дейч М.Е. Техническая газодинамика. Изд. 2-е, переработ. М.-Л. Госэнергоиздат, 1961, с черт., ил.