Досліди Рейнольдса

Дослідами Рейнольдса встановлено, що за певних граничних умов у кожному потоці є "точка переходу", яка відповідає зміні одного режиму іншим. Ця точка переходу за Рейнольдсом визначається безрозмірним комплексом - числом Рейнольдса [math]\operatorname{Re}[/math], яке називається критичним числом Рейнольдса. Рух буде ламінарний, коли [math]\operatorname{Re} \lt {\operatorname{Re} _{kr}}[/math]. Якщо [math]\operatorname{Re} \gt {\operatorname{Re} _{kr}}[/math], то потік стає нестаціонарним і переходить у турбулентний режим. При русі рідини у прямоліній циліндричній трубі [math]\operatorname{Re} _{kr} = 2300[/math]. Для кожного конкретного випадку руху число Рейнольдса має своє критичне значення.

Історія дослідження

Ще у минулому столітті було зауважено, що при русі рідини можуть бути два принципово різні режими руху рідини - ламінарний і турбулентний ( слово "ламінарний" походить від латинського "lamina", що означає "шаруватий"; турбулентний - від латинського "turbulentus", що означає вихровий, безладний.) На принципову різницю ламінарного і турбулентного руху рідини звернув увагу Д.І. Менделєєв у 1880 р. і М.П. Петров у 1883 р. Однак найбільш глибоко і повно це питання було досліджене у 1883 р. англійським фізиком О.Рейнольдсом. Після Рейнольдса багатьма дослідниками було виконано ряд теоретичних та експерементальних праць щодо вивчення переходу ламінарного режиму в турбулентний, і навпаки, в різних умовах. Незважаючи на це, дане питання і на цей час вивчене недостатньо; багато питань переходу одного режиму в інший та природа турбулентного режиму залишаються і тепер не зовсім зрозумілими.

Ламінарний і турбулентний режмим руху

Схематичний вигляд ламінарного руху

Гідравлічна структура потоків при цих двох режимах істотно відрізняється. При ламінарному режимі окремі частинки рідини переміщються паралельно одна одній і окремі струминки потоку переміщуються упорядковано. При цьому режимі течій в циліндричних шарів, які, подібно до окремих частин телескопічної труби, переміщуються. Ламінарний рух рідин зустрічається в трубках невеликого діаметра при переміщенні дуже в'язких рідин. В інженерній практиці у більшості випадків спостерігається рух рідини при турбулентному режимі, характреною ознакою якого є безладний характер переміщення окремих частинок. При турбулентному режимі в кожній точці простору, зайнятого рідиною, що рухається, відбувається безперервна зміна швидкості як за значенням, так і за напрямком.Така зміна швидкості називається пульсацією швидкості, яка, в свою чергу, викликає пульсацію тиску. У зв'язку з цим турбулентний потік - це безліч мас, які інтенсивно обертаються і переміщуються, при загальному поступальному русі.

Експеримент Рейнольдса

Дослід Рейнольдса

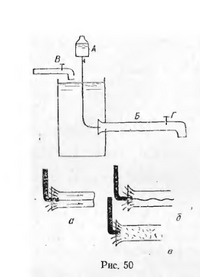
Експеримент Рейнольдса полягав у введені барвника з посудини А (рис.50) у скляну трубу Б і спостереженні за течією окремих струминок. Було виявлено, що за певних умов забарвлена струминка рухається прямолінійно, без змішування з навколишньою масою рідини. Інакше кажучи, спостерігався ламінарний рух (рис. 50,а). Далі збільшення швидкості (шляхом відповідного регулювання вентилями В і Г) приводить до зміни характеру руху частинок рідини. Забарвлена струминка зі збільшенням шивдкості стає звивистою (рис. 50,б), хиткою, в окремих місцях уривчастою, а відтак повністю розмивається і зміщується з усією масою рідини, що рухається в трубі (рис. 50,в). Виникає турбулентний режим з притаманним йому інтенсивним переміщенням частинок рідини по всьому перерізу потоку.

Результати багатьох досліджень показують, що ламінарний рух у певних умовах стає нестабільним і переходить у турбулентний під впливом навіть незначних зовнішніх збурень. Ламінарний режим переходит у турбулентний через так званий перехідний режим, а сам процес переходу в більшості випадків можна розглядати як безперервний коливний процес.

На величину [math]\operatorname{Re} _{kr}[/math] впливає ряд факторів: умова входу в трубу, знак прискорення, з яким рухається рідина, кривина труби тощо.Наприклад, [math]\operatorname{Re} _{kr}[/math] значно знижується навіть при невеликому викривленні труби. Місця розширення трубопроводу або русел мають підвищену схильність до порушення ламінарного режиму.

Ретельно усунувши збурення при вході в трубу (рис. 50, вузол Д), можна значно збільшити критичне число Рейнольдса (навіть до 20000 і вище). У зв'язку з цим деколи вводять поняття про нижнє і верхнє число Рейнольдса: при цьому під нижнім критичним числом розуміють нижню границю [math]\operatorname{Re}[/math] для турбулентного руху, а під верхнім - верхню границю для ламінарного руху. Значення [math]\operatorname{Re} _{kr} = 2300[/math] приймається за нижню границю для турбулентного руху, а [math]\operatorname{Re} _{kr} = 4000...20000[/math] дає діапазон зміни верхнього критичного числа [math]\operatorname{Re} _{kr}[/math].

При [math]\operatorname{Re} \lt {\operatorname{Re} _{kr}}[/math] будь-якого роду збурення в потоці гасяться силами в'язкості і ламінарний режим в цілому стійкий, а турбулентний - нестійкий. При [math]\operatorname{Re} \gt {\operatorname{Re} _{kr}}[/math], навпаки, турбулентний режим стійкий, а ламінарний - нестійкий. Далі під критичним числом [math]\operatorname{Re} _{kr}[/math] будемо розуміти тільки нижнє критичне число. Звернемо увагу на те, що для труб некруглого перерізу, відкритих русел, лотків число Рейнольдса виражається через гідравлічний радіус [math]\operatorname{R}[/math], тобто У даному разі критичне число [math]\operatorname{Re} _{kr} = 580[/math]

Число Рейнольдса

Знайти число Рейнольдса можна за формулою

[math]\operatorname{Re} = \frac{{\rho VL}}{\eta } = \frac{{VL}}{\nu } = \frac{{QL}}{{\nu A}}[/math]

Література

• Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с.

• Т.М. Башта, С.С Руднев Гидравлика, гидромашины и гидроприводы,1982.-423с

• Френкель Н.З. Гидравлика 1956.-456с

• Кочин Н.Е Теоретическая гидромеханика.Часть 1-2,1963-585с