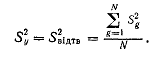Відмінності між версіями «Планування другого порядку»
Ihor p (обговорення • внесок) |
Ihor p (обговорення • внесок) |
||
| Рядок 51: | Рядок 51: | ||
<center>[[Файл:formula7.gif]]</center> | <center>[[Файл:formula7.gif]]</center> | ||
| + | |||
| + | Перед реалізацією проводиться рандомізація рядків матриці планування. | ||
| + | Перевірка відтворюваності, як і в ПФЕ, виконується за критерієм Кохрена, після чого обчислюється оцінка дисперсії відтворюваності | ||
| + | |||
| + | <center>[[Файл:formula8.gif]]</center> | ||
Версія за 14:37, 5 березня 2010
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
.................... Презентація доповіді (університетський репозиторій).
Планування другого порядку
Планування другого порядку застосовується для математичного опису об'єкта поблизу екстремальної точки статистичної характеристики або тоді, коли необхідний точніший опис в інших точках факторного простору. При цьому використовують поліном другого порядку:
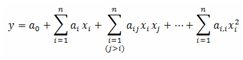
Задача, як і в ПФЕ, полягає у визначенні методом найменших квадратів за результатами спланованого експерименту коефіцієнтів цього рівня за умови, що виконуються передумови регресійного аналізу. ПФЕ типу [math]2^n[/math] дає змогу дістати роздільні оцінки як лінійних коефіцієнтів bi (після переходу до безрозмірних z), так і коефіцієнтів парних взаємодій bij. Точки ПФЕ лежать у вершині n-вимірного куба. Вектор-стовпці лінійних факторів матриці планування ортогональні між собою, тобто виконується умова
З теорії інтерполяції (апроксимації) відомо, що для розв'язання задачі знаходження роздільних оцінок параметрів апроксимуючого виразу число рівнів для кожної із змінних повинно бути на одиницю більше ступеня апроксимуючого полінома, тобто для полінома другого порядку число рівнів дорівнює трьом. Однак, як показали дослідження, ПФЕ типу [math]3^n[/math] (планування на трьох рівнях) не є раціональним через велике число дослідів. Задача розв'язується іншим способом. До ПФЕ типу [math]2^n[/math] додають центральну точку з координатами (0, 0, ..., 0) і зіркові точки з координатами (0, 0, ..., ±α), які лежать на сфері діаметра 2α (рис. 1). Зіркові точки будують на осях факторного простору. Вибір відстані від нульової точки до зіркової, яка визначається плечем α, залежить від критерію оптимальності плану.
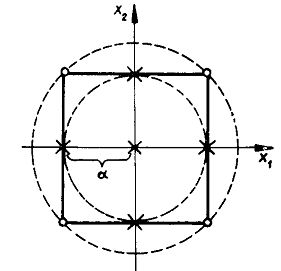
Розглянемо планування, оптимальне з точки зору незалежності оцінок bi,i Його називають ортогональним центральним композиційним плануванням (ОЦКП), тобто планом, в якому критерієм оптимальності є ортогональність стовпців матриці планування. Композиційним таке планування, як й інші форми планування другого порядку, називається тому, що новий план дістають шляхом компонування первинного двофакторного плану з деякою кількістю додаткових точок. Оскільки в числі цих додаткових точок обов'язково фігурує центральна, в якій всі змінні хi мають середній рівень, а zi=0, плани називають центральними. Ортогональність матриці композиційного планування забезпечується виконанням рівностей
де і-номер фактора; j-номер рядка; g-номер досліду. Для ортогоналізації першого з цих співвідношень застосовується перехід до нової змінної
де N-загальне число експериментів. Величина zi залежить тільки від числа факторів n і числа дослідів N, яке звичайно вибирається так, що
де Nn = [math]2^n[/math]-кількість вершин гіперкуба при ПФЕ; Nα = 2n-число зіркових точок; N0= 1- число дослідів у центрі плану. Якщо N вибрати так, то zi визначають за формулою
Тому ортогоналізація другої з вищенаведених умов досягається вибором бажаного α. Для зручності підготовки і планування величини α, N, Nn, Nα обчислені і табульовані залежно від числа факторів (табл. 1).
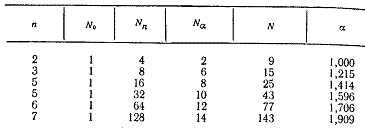
Сформуємо матриці ОЦКП для двох факторів. При n = 2 отримаємо α = 1,0 (див. табл. 1), для обчислення скористаємося наведеними формулами. Оскільки [math]z1^2=(4+2)/9=0,667[/math], то стовпець добувається відніманням одного і того ж числа 0,67 від числа стовпця [math]zi^2[/math] того ж рядка (табл. 2).
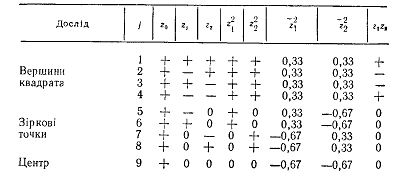
Реалізація експериментів за ОЦКП здійснюється за тією ж методикою, що і ПФЕ. Таким чином, через випадковий характер зміни вихідної величини у у кожній точці хg проводиться m паралельних дослідів і обчислюється середнє значення функції відклику
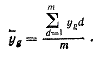
Перед реалізацією проводиться рандомізація рядків матриці планування. Перевірка відтворюваності, як і в ПФЕ, виконується за критерієм Кохрена, після чого обчислюється оцінка дисперсії відтворюваності