Відмінності між версіями «Користувач:Valdemar88»
 
(Не показані 4 проміжні версії цього користувача)
Рядок 1: Рядок 1:
−
== Закон Бернуллі ==
+
'''Рівня́ння Берну́ллі''' — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю '''v''' рідини, тиском '''p''' в ній та висотою '''h''' частинок над площиною відліку.
−
Інтегра́л Берну́ллі рівнянь гідродинаміки&nbsp;— це інтеграл, що визначає в кожній точці потоку ідеальної рідини або баротропного газу тиск <math>p</math>, що встановився: (<math>p=F(\rho)</math>) через швидкість <math> \vec v</math> потоку у відповідній точці та через силову функцію <math> \vec u(x,y,z)</math> об'ємних сил:<br />
+
Встановив його у 1738 р. Бернуллі Даніель Д. Бернуллі.
−
<math>\int \frac{dp}{\rho}\ = C - \frac{1}{2}\left | \vec v^2 \right | +  \vec u</math> <br />
 
−
Стала <math>C</math> має для кожної лінії струменю своє значення, що змінюється з переходом від одної лінії струменю до іншої. Якщо рух потенційний, то стала <math>C</math> одна і таж для всього потоку.<br />
 
−
Для руху, що не встановився, інтеграл Бернулі (називають інколи ''інтегралом Коші—Лагранжа'') має місце за наявності потенціалу швидкостей:<br />
 
−
<math>\int \frac{dp}{\rho}\ = \frac{\partial \phi}{ \partial t} - \frac{1}{2}\left | \vec v^2 \right | +  \vec u + f(t)</math>, <br />
 
−
причому <math> \mathbf{v} = \text{grad}\, \phi(x,y,z,t)</math> а <math>f(t)</math>&nbsp;— довільна функція часу.<br />
 
−
Для нестискуваних рідин ліва частина рівнянь приводиться до вигляду <math>\frac{p}{\rho}</math> для баротропного газу (<math>p=F(\rho)</math>)&nbsp;— до вигляду:<br />
 
−
<math>\int \frac{dp}{\rho}\ =  \int F'(\rho) \frac{d \rho}{\rho}\ </math> <br />
 
−
Інтеграл Бернулі запропоновано Бернуллі Даніель ( <u>1738</u>)
 
  
 +
Для ламінарної течії ідеальної (нестисненої) рідини рівняння Бернуллі має вигляд:
 +
''':<math>h+\frac{v^{2}}{2g}+\frac{p}{\rho g}=\text{const}</math>'''
  
−
'''Закон Бернулли''' является следствием [[закон сохранения энергии|закона сохранения энергии]] для стационарного потока [[идеальная жидкость|идеальной]] (то есть без внутреннего трения) несжимаемой жидкости:
+
або<br />
−
: <math>\tfrac{\rho v^2}{2} + \rho g h + p = \mathrm{const}</math>
+
:<math>h\rho g+p+\frac{\rho v^{2}}{2}=\text{const}</math>,
−
Здесь
 
−
: <math>~\rho</math> — [[плотность]] жидкости,
 
−
: <math>~v</math> — [[скорость]] потока,
 
−
: <math>~h</math> — [[высота]], на которой находится рассматриваемый элемент жидкости,
 
−
: <math>~p</math> — [[давление]] в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
 
−
: <math>~g</math> — [[ускорение свободного падения]].
 
  
−
Константа в правой части обычно называется ''напором'', или полным давлением, а также '''интегралом Бернулли'''. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.
+
де ρ — густина рідини; g — прискорення вільного падіння.
  
−
Это соотношение, выведенное [[Даниил Бернулли|Даниилом Бернулли]] в [[1738 год в науке|1738]] г., было названо в его честь ''уравнением Бернулли''. (Не путать с [[Дифференциальное уравнение Бернулли|дифференциальным уравнением Бернулли]].)
+
В останньому рівнянні всі члени мають розмірність тиску, p — статичний тиск; <math>\frac{\rho v^{2}}{2}</math> — динамічний тиск; hρg — ваговий тиск.
 +
[[Файл:BernoullisLawDerivationDiagram.png|thumb|400px]]
 +
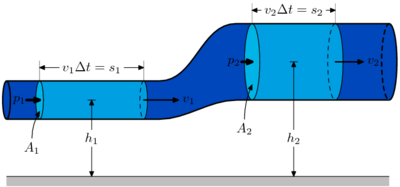
Якщо такі рівняння записати для двох перерізів течії, то матимемо:
 +
:<math>\frac{v_{1}^{2}}{2}+g h_{1}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+g h_{2}+\frac{p_{2}}{\rho}</math>
  
−
Для горизонтальной трубы <math>h=0</math> и уравнение Бернулли принимает вид:&nbsp;&nbsp; <math>\tfrac{\rho v^2}{2}+p=\mathrm{const}</math>.
+
Для горизонтальної течії середні члени у лівій і правій частині рівняння скорочуються і воно набуває вигляду:
 +
:<math>\frac{v_{1}^{2}}{2}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+\frac{p_{2}}{\rho}</math>
  
−
Эта форма уравнения Бернулли может быть получена путём интегрирования [[Уравнение Эйлера|уравнения Эйлера]] для стационарного одномерного потока жидкости, при постоянной плотности <big><math>\rho</math></big>:&nbsp;&nbsp; <math>v\tfrac{dv}{dx}=-\tfrac {1}{\rho}\cdot \tfrac {dp}{dx}</math>.
+
тобто в усталеній горизонтальній течії ідеальної нестисненої рідини в кожному її перерізі сума статичного і динамічного тисків буде сталою. Отже, в тих місцях течії, де швидкість рідини більша (вузькі перерізи), її динамічний тиск збільшується, а статичний зменшується. На цьому явищі заснована дія струминних насосів, ежекторів, витратомірів Вентурі і Піко, пульверизаторів.
  
−
[[Файл:BernoullisLawDerivationDiagram.png |thumb|400px|right]]
+
Рівняння Бернуллі є наслідком закону збереження енергії. Якщо рідина не ідеальна, то її механічна енергія розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає. Для реальної в'язкої рідини в правій частині рівнянь, слід додати величину втрат тиску '''Δр<sub>вт</sub>''' на гідравлічний опір рухові.
  
−
Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
+
Рівняння Бернуллі широко застосовують для розв'язання багатьох гідравлічних задач у нафтогазовій справі.
  
−
'''Полное давление''' состоит из весового <math>(\rho g h)</math>, статического <math>(p)</math> и динамического <math>\left(\tfrac{\rho v^2}{2}\right)</math> давлений.
+
== Приклади застосування закону Бернуллі ==
 +
Трубка Вентурі застосовується для вимірювання швидкості у трубах за допомогою вимірювання тиску у двох різних точках трубопроводу та, таким чином, допомагає запобігти наслідкам кавітації. Трубка Вентурі поступово звужує діаметр трубопроводу. Такий звужувальний отвір обмежує потік рідини, що зумовлює різницю тисків у точках вимірювання (на початку звуження та у найвужчій частині).  Базується дане вимірювання на ефекті Вентурі, формулу для якого можна отримати із рівняння безперервності та закону Бернуллі:
 +
V<sub>1</sub>S<sub>1</sub>=V<sub>2</sub>S2 (де S – площа взаємодії рідини з поверхнею трубки), V1=(S<sub>2</sub>/S<sub>1</sub>)V<sub>2</sub>;
 +
p<sub>1</sub> - p<sub>2</sub>= ρ/2 (V<sub>2</sub><sup>2</sup> - V<sub>1</sub><sup>2</sup>) = ρ/2 (V<sub>2</sub><sup>2</sup> – [(S<sub>2</sub>/S<sub>1</sub>)V<sub>2</sub>]<sup>2</sup>);
 +
V<sub></sub> = S1√((2(p<sub>1</sub> - p<sub>2</sub>))/(ρ(S<sub>1</sub><sup>2</sup>-S<sub>2</sub><sup>2</sup>))).
 +
==== Трубка Піто ====
 +
Трубка Піто застосовується для вимірювання різниці тисків у двох точках, тобто за допомогою цієї трубки можна знайти динамічний тиск. Для рідин та газів відіграє роль манометра, один кінець якого спрямовано назустріч потоку, а інший виступає з нього та приєднаний до приладу, який вимірює тиск. Має вигляд букви “L”. Якщо перед отвором A швидкість зменшується до значення V<sub>2</sub> = 0, то
 +
p<sub>2</sub> – p<sub>1</sub> = ρ/2 V<sub>1</sub><sup>2</sup>.
 +
При встановленні надлишкового тиску у трубці надлишковий тиск обчислюється за формулою
 +
p = ζ(V<sub>0</sub><sup>2</sup>ρ)/2,
 +
де ζ – коефіцієнт, V0 – швидкість налітаючого вихору.
 +
==== Формула Торрічеллі ====
 +
Закон Торрічеллі показує, що при витіканні ідеальної нестискувальної рідини зі щілини у боковій стінці або на дні посудини рідина набуває швидкості тіла, що падає з певної висоти. За допомогою цього можна обчислити максимальний рівень витоку рідини з посудини. Для підтвердження можна скористатись законом Бернуллі, вивівши з нього формулу Торрічеллі:
 +
ρgh + p<sub>0</sub> = (pV<sup>2</sup>)/2 + p<sub>0</sub>,
 +
де p0 – атмосферний тиск, h – висота стовпу рідини у посудині, V – швидкість витікання рідини. Звідси
 +
V = √2gh.
  
−
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной [[Эффект Магнуса|эффекта Магнуса]]. Закон Бернулли справедлив и для [[Ламинарное течение|ламинарных]] потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода [[расходомер]]ов (например [[труба Вентури]]), водо- и пароструйных [[насос]]ов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — [[Гидравлика|гидравлики]].
+
=== У техніці та побуті ===
 +
==== Пульверизатор ====
 +
У пульверизаторі застосовується головний наслідок закону Бернуллі: зі зростанням швидкості відбувається зростання динамічного тиску та спадання статичного тиску. У капіляри пульверизатора вдувається повітря або пара. Вдування знижує атмосферний тиск у капілярі, і рідина з балону пульверизатора під дією більшого атмосферного тиску піднімається по капіляру. Там вона роздроблюється струменем повітря.
 +
==== Водоструминний насос ====
 +
Водоструминний насос – резервуар, у який впаяні дві трубки. Під дією тиску у першу трубку протікає вода, потрапляючи потім у другу трубку. У звуженій частині першої трубки виникає зменшений тиск, який менший за атмосферний. Тому у резервуарі створюється напруження. Трубку приєднують до резервуару, який проходить у посудину, з якої необхідно відкачати повітря.
 +
==== Карбюратор ====
 +
Карбюратор – пристрій у системі живлення карбюраторних двигунів внутрішнього згоряння, що застосовується для змішування бензину та повітря. Під час руху поршня у такті впускання тиск у циліндрі знижується. При цьому навколишнє повітря всмоктується циліндром через повітряну трубу карбюратора&nbsp;— дифузор. У найвужчій частині дифузора, де тиск відповідно найменший, розташовано розпилювач, із якого витікає паливо. Паливо подрібнюється струменем повітря на маленькі краплі, і утворюється горюча суміш.
 +
==== Осушування боліт ====
 +
Осушування боліт за принципом закону Бернуллі проводилося дуже давно. До болота підводили канали від найближчої річки. Внаслідок великої різниці тисків між водою з болота та водою з каналу вода з каналу “всмоктувала” воду з болота.
 +
==== Ракета ====
 +
У конструюванні ракет також застосовується закон Бернуллі. Для створення тяги у ракеті використовується паливо, яке спалюють у камері згоряння. Гази утворюють реактивний струмінь, який прискорюється, коли проходить через спеціальне звуження – сопло. Са́ме звуження сопла і є основною причиною прискорення реактивного струменя газів і збільшення реактивної тяги.
 +
==== Свисток ====
 +
Свисток являє собою приклад використання закону Бернуллі у газоструменевих випромінювачах звукових хвиль.
 +
Вихровий свисток являє собою циліндричну камеру, у подається потік повітря через тангенціально розташовану трубку. Утворений вихровий потік надходить у вихідну трубку меншого діаметру, яка розташована на осі. Там інтенсивність вихору різко підвищується та тиск в його центрі стає значно нижче атмосферного. Перепад тиску періодично вирівнюється за рахунок прориву газів з атмосфери у вихідну трубку та руйнування вихору.
 +
==== Диск Релея ====
 +
Диск Релея – прилад для вимірювання коливальної швидкості частинок у звуковій хвилі та сили звуку.
 +
Являє собою тонку пластинку круглої форми, із слюди або металу, підвішену на тонку кварцеву нитку. Зазвичай диск розміщують під кутом у 45º до напряму коливань частинок середовища, оскільки таке розташування найбільш чутливе до коливань. При розповсюдженні звукових хвиль диск повертається перпендикулярно до напряму коливань. Це відбувається через те, що при обтіканні пластинки тиск, згідно із законом Бернуллі більший у тому місці, де швидкість менша. Сили тиску уворюють обертальний момент, який урівноважується за рахунок пружності нитки. При цьому диск встановлюється до напряму потоку під кутом, що більший, ніж 45º. за кутом повороту диску визначають силу звуку. У постійному потоці кут повороту диска Релея пропорційний квадрату швидкості, при звукових коливаннях – квадрату амплітуди швидкості, і цей кут не залежить від частоти.
  
−
Закон Бернулли справедлив в чистом виде только для жидкостей, [[вязкость]] которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела почти всегда в точности равна нулю (кроме случаев отрыва струй при некоторых редких условиях).
+
== Неправильне застосування закону Бернуллі ==
−
 
+
Підіймальна сила літака зумовлюється специфічною будовою крила. Донедавна для пояснення причини підіймальної сили крила застосовували закон Бернуллі. Відповідно до закону Бернуллі, пояснення підіймальної сили літака виглядає так: крило має особливу будову – знизу воно має пряме, а його верхня частина заокруглена. Це дозволяє збільшити площу верхньої частини крила. Згідно із законом Бернуллі, із збільшенням швидкості тиск зменшується. А оскільки повітря долає шлях під крилом та над крилом за однаковий проміжок часу, під крилом виникає область із збільшеним тиском, що зумовлює підйом літака у повітря. Таким чином виникає підйомна сила.<br/>
−
== Одно из применений ==
+
Проте, згідно з сучасними уявленнями, підіймальна сила крила виникає не внаслідок закону Бернуллі. Рух повітряної маси перед крилом можна вважати суцільним, він характеризується одним показником швидкості. Коли повітряна маса контактує з крилом, вона розбивається на дві частини, які, внаслідок форми крила, мають різні швидкості і це зумовлює різний тиск. Однак це не може бути причиною підйомної сили, оскільки ці дві повітряні маси обтікають відповідно верхню і нижню частини крила не за однаковий час, бо, на відміну від колишніх уявлень, ці повітряні потоки не поєднуються на кінці крила. Отже, більша довжина верхньої частини крила не означає більшої швидкості руху повітря. Отже, хоча закон Бернуллі і можна застосувати для повітряних мас, які розсікаються крилом (більша швидкість зумовлює менший тиск), проте він один не пояснює підіймальну силу крила. Для повного пояснення слід застосовувати теорему Жуковського.
−
Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.
 
−
 
 
−
[[Файл:ЭФФЕКТ_ВЕНТУРИ.GIF|thumb|Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости <math>\Delta h</math>; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли]]
 
−
 
 
−
Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:
 
−
: <math>\rho g h + p_0 = \frac{\rho v^2}{2} + p_0</math>,
 
−
где
 
−
: <math>p_0</math> — [[атмосферное давление]],
 
−
: <math>h</math> — высота столба жидкости в сосуде,
 
−
: <math>v</math> — скорость истечения жидкости,
 
−
: <math>z\, +\, \frac{p}{\rho g}</math> — гидростатический напор (сумма геометрического напора ''z'' и пьезометрической высоты <math> \frac{p}{\rho g}</math>).
 
−
 
 
−
Отсюда: <math>v = \sqrt{2gh}</math>. Это — формула [[Торричелли]]. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты <math>h</math>.
 
−
 
 
−
Часто уравнение Бернулли записывается в виде:
 
−
 
 
−
: <math>Hd\, =\, z\, +\, \frac{p}{\rho g}\, +\, \frac{v^2}{2\,g}=\, \text{const}\,</math>
 
−
 
 
−
где
 
−
: <math>Hd\,</math> — гидродинамический напор,
 
−
:: <math> \frac{v^2}{2\,g}</math> — скоростной напор.
 
−
 
 
−
== Для сжимаемого идеального газа ==
 
−
 
 
−
 
 
−
: <math>\frac {v^2}{2}+ gh+\left(\frac {\gamma}{\gamma-1}\right)\frac {p}{\rho}  = \mathrm{const}</math><ref>Clancy, L.J., ''Aerodynamics'', Section 3.11</ref> (постоянна вдоль линии тока или линии вихря)
 
−
 
 
−
где
 
−
: <math>\gamma = \frac{C_p}{C_V}</math> — [[Показатель адиабаты|Адиабатическая постоянная]] газа
 
−
: <math>p</math> — [[давление]] газа в точке
 
−
: <math>\rho</math> — плотность газа в точке
 
−
: <math>v</math> — скорость течения газа
 
−
: <math>g</math> — [[ускорение свободного падения]]
 
−
: <math>h</math> — высота относительно начала координат
 
−
 
 
−
При движении в неоднородном поле <math>gh</math> заменяется на [[потенциал]] гравитационного поля.
 
−
 
 
−
== Термодинамика закона Бернулли ==
 
−
Из [[Статистическая физика|статистической физики]] следует, что на линиях тока при адиабатическом течении остается постоянным следующее соотношение:
 
−
: <math>  \frac{v^2}{2} + w + \varphi = \mathrm{const} </math>
 
−
где <math> w </math> — [[энтальпия]] единицы массы, <math> \varphi</math> — потенциал силы.
 
−
{{Hider|
 
−
  title = Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений |
 
−
  hidden =1 |
 
−
  content =
 
−
1. Запишем [[Уравнение Эйлера]]:
 
−
: <math> \rho \frac{\partial \vec v}{\partial t} + \rho (\vec v, \nabla) \vec v = - \nabla p - \rho \nabla \varphi </math>
 
−
:: <math> \varphi </math> — потенциал. Для силы тяжести <math> \varphi = gz </math>
 
−
2. Запишем выражение для [[Энтальпия|энтальпии]] и предположим, что [[энтропия]] системы постоянна (или, можно сказать, что [[Адиабатический процесс|течение адиабатично]]):
 
−
: <math> dW = V dP + T dS</math>
 
−
Пусть <math> S=const</math> и <math> w </math> — энтальпия единицы массы, тогда:
 
−
: <math> dw = \frac{dp}{\rho}</math>
 
−
или
 
−
: <math> \nabla w = \frac{\nabla p}{\rho}</math>
 
−
3. Воспользуемся следующими соотношениями из [[Векторная алгебра|векторной алгебры]]:
 
−
: <math> \frac 12 \nabla v^2 = (\vec v, \nabla) \vec v + \vec v \times \operatorname{rot}\vec v </math>
 
−
: <math> \vec l \cdot \nabla = \frac{\partial}{\partial l}</math> — проекция градиента на некоторое направление равно производной по этому направлению.
 
−
4. Уравнение Эйлера с использованием соотношений выведенных выше:
 
−
: <math> \rho \frac{\partial \vec v}{\partial t} + \rho \left[ \frac 12 \nabla v^2 - \vec v \times \operatorname{rot}\vec v  \right] = - \rho \nabla (\varphi + w) </math>
 
−
Спроецируем это уравнение на единичный вектор касательный к [[Линия тока|линии тока]], учитывая следующее:
 
−
:: <math> \frac{\partial \vec v}{\partial t} = 0 </math> — условие стационарности
 
−
:: <math> (\vec l , \vec v \times \operatorname{rot}\vec v ) = 0 </math> — так как <math> \vec l ||\vec v </math>
 
−
Получаем:
 
−
: <math> \frac{\partial}{\partial l} \left( \frac{v^2}{2} + w + \varphi \right) = 0 </math>
 
−
То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:
 
−
: <math>  \frac{v^2}{2} + w + \varphi = \operatorname{const} </math>
 
−
|
 
−
  title-style = color: black;  font-weight: bold; text-align: left;|
 
−
  content-style = color: black;  text-align: left; |
 
−
}}
 
−
 
 
−
== Практические следствия ==
 
−
* закон Бернулли объясняет эффект притяжения между телами, находящимися на границе потока движущейся жидкости (газа). Иногда это притяжение может создавать угрозу безопасности. Например, при движении  [[Электропоезд «Сапсан»|скоростного поезда «Сапсан»]] (скорость движения более 200 км/час) для людей на платформах возникает опасность сброса под поезд<ref>[http://www.bbc.co.uk/russian/russia/2010/03/100326_sapsan_stones.shtml Би-Би-Си: «Камни для „Сапсана“, или „месть бедных“»]</ref>. Аналогично «затягивающая сила» возникает при движении судов параллельным курсом: например, подобные инциденты происходили с лайнером «[[Олимпик (лайнер)#Вторая неудача — инцидент с крейсером «Хоук»|Олимпик]]».
 
−
 
 
−
== Приложение ==
 
−
{{Hider|
 
−
  title = Вывод уравнения Бернулли  |
 
−
  hidden =1 |
 
−
  content =
 
−
: Энергия маленького элемента жидкости: <math>E=\frac{mv^2}2+U</math> (U - потенциальная энергия)
 
−
: Слева на большой объем жидкости между двумя поверхностями действует сила <math>p_1\cdot S_1</math>, а справа - <math>-p_2\cdot S_2</math> (минус, потому что влево).
 
−
: Итак, этот объем жидкости сдвинулся (за время <math>dt</math>). Пусть его левая граница сдвинулась на <math>dl_1</math>, а правая - на <math>dl_2</math>.
 
−
: Пишем условие несжимаемости: <math>S_1\cdot dl_1=V_1=V_2=S_2\cdot dl_2</math>. Объёмы, как видно, бесконечно малые, дифференциальные. Их самих можно рассматривать как дифференциалы объёма всего большого элемента.
 
−
: Далее. Сначала наш большой элемент состоял из левого голубого элемента и средней синей части. Теперь он состоит из средней синей части и правого голубого элемента. При этом все его молекулы сдвинулись, но так как течение стационарное, то в каждой точке со временем энергия не меняется. Поэтому энергия средней синей части не поменялась. Поэтому работа сил (ну, или за бесконечно малое время не сама работа, а её дифференциал) равна изменению энергии, равному, в свою очередь, энергии правого голубого элементика (который добавился) минус энергия левого голубого элементика (который, наоборот, ушёл, влился в средний синий). <math>p_1\cdot S_1\cdot dl_1 - p_2\cdot S_2\cdot dl_2 = dA = E_2-E_1 = \frac{m_2\cdot v_2^2}2+U_2-\frac{m_1\cdot v_1^2}2-U_1 = \frac{\rho V_2v_2^2}2+U_2-\frac{\rho V_1v_1^2}2-U_1</math>.
 
−
: Теперь вспоминаем формулу несжимаемости и сокращаем на объём. <math>p_1-p_2 = \frac{\rho v_2^2}2-\frac{\rho v_1^2}2+{U_2\over V_2}-{U_1\over V_1}</math>.
 
−
: Сгруппируя слагаемые, получаем формулу Бернулли: <math>p_1+{U_1\over V_1}+\frac{\rho v_1^2}2 = p_2+{U_2\over V_2}+\frac{\rho v_2^2}2</math>, или просто <math>p+\frac UV+\frac{\rho v^2}2=const</math>, или, подставив потенциальную энергию, <math>p+\rho gh+\frac{\rho v^2}2=const</math>.
 
−
|
 
−
  title-style = color: black;  font-weight: bold; text-align: left;|
 
−
  content-style = color: black;  text-align: left; |
 
−
}}
 
−
 
 
−
 
 
−
 
 
−
== Литература ==
 
−
* {{Книга:Ландау Л.Д., Лифшиц Е.М.: Гидродинамика|2003}}
 
−
 
 
−
 
 
−
 
 
−
 
 
−
== Література ==
 
−
 
 
−
''Милн-Томсон Л. М.'' «Теоретическая гидродинамика». пер. з англ., М., 1964
 
−
 
 
−
[[Категорія:гідродинаміка]]
 

Поточна версія на 22:07, 10 квітня 2011

Рівня́ння Берну́ллі — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю v рідини, тиском p в ній та висотою h частинок над площиною відліку. Встановив його у 1738 р. Бернуллі Даніель Д. Бернуллі.

Для ламінарної течії ідеальної (нестисненої) рідини рівняння Бернуллі має вигляд: :[math]h+\frac{v^{2}}{2g}+\frac{p}{\rho g}=\text{const}[/math]

або

[math]h\rho g+p+\frac{\rho v^{2}}{2}=\text{const}[/math],

де ρ — густина рідини; g — прискорення вільного падіння.

В останньому рівнянні всі члени мають розмірність тиску, p — статичний тиск; [math]\frac{\rho v^{2}}{2}[/math] — динамічний тиск; hρg — ваговий тиск.

BernoullisLawDerivationDiagram.png

Якщо такі рівняння записати для двох перерізів течії, то матимемо:

[math]\frac{v_{1}^{2}}{2}+g h_{1}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+g h_{2}+\frac{p_{2}}{\rho}[/math]

Для горизонтальної течії середні члени у лівій і правій частині рівняння скорочуються і воно набуває вигляду:

[math]\frac{v_{1}^{2}}{2}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+\frac{p_{2}}{\rho}[/math]

тобто в усталеній горизонтальній течії ідеальної нестисненої рідини в кожному її перерізі сума статичного і динамічного тисків буде сталою. Отже, в тих місцях течії, де швидкість рідини більша (вузькі перерізи), її динамічний тиск збільшується, а статичний зменшується. На цьому явищі заснована дія струминних насосів, ежекторів, витратомірів Вентурі і Піко, пульверизаторів.

Рівняння Бернуллі є наслідком закону збереження енергії. Якщо рідина не ідеальна, то її механічна енергія розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає. Для реальної в'язкої рідини в правій частині рівнянь, слід додати величину втрат тиску Δрвт на гідравлічний опір рухові.

Рівняння Бернуллі широко застосовують для розв'язання багатьох гідравлічних задач у нафтогазовій справі.

Приклади застосування закону Бернуллі

Трубка Вентурі застосовується для вимірювання швидкості у трубах за допомогою вимірювання тиску у двох різних точках трубопроводу та, таким чином, допомагає запобігти наслідкам кавітації. Трубка Вентурі поступово звужує діаметр трубопроводу. Такий звужувальний отвір обмежує потік рідини, що зумовлює різницю тисків у точках вимірювання (на початку звуження та у найвужчій частині). Базується дане вимірювання на ефекті Вентурі, формулу для якого можна отримати із рівняння безперервності та закону Бернуллі: V1S1=V2S2 (де S – площа взаємодії рідини з поверхнею трубки), V1=(S2/S1)V2; p1 - p2= ρ/2 (V22 - V12) = ρ/2 (V22 – [(S2/S1)V2]2); V = S1√((2(p1 - p2))/(ρ(S12-S22))).

Трубка Піто

Трубка Піто застосовується для вимірювання різниці тисків у двох точках, тобто за допомогою цієї трубки можна знайти динамічний тиск. Для рідин та газів відіграє роль манометра, один кінець якого спрямовано назустріч потоку, а інший виступає з нього та приєднаний до приладу, який вимірює тиск. Має вигляд букви “L”. Якщо перед отвором A швидкість зменшується до значення V2 = 0, то p2 – p1 = ρ/2 V12. При встановленні надлишкового тиску у трубці надлишковий тиск обчислюється за формулою p = ζ(V02ρ)/2, де ζ – коефіцієнт, V0 – швидкість налітаючого вихору.

Формула Торрічеллі

Закон Торрічеллі показує, що при витіканні ідеальної нестискувальної рідини зі щілини у боковій стінці або на дні посудини рідина набуває швидкості тіла, що падає з певної висоти. За допомогою цього можна обчислити максимальний рівень витоку рідини з посудини. Для підтвердження можна скористатись законом Бернуллі, вивівши з нього формулу Торрічеллі: ρgh + p0 = (pV2)/2 + p0, де p0 – атмосферний тиск, h – висота стовпу рідини у посудині, V – швидкість витікання рідини. Звідси V = √2gh.

У техніці та побуті

Пульверизатор

У пульверизаторі застосовується головний наслідок закону Бернуллі: зі зростанням швидкості відбувається зростання динамічного тиску та спадання статичного тиску. У капіляри пульверизатора вдувається повітря або пара. Вдування знижує атмосферний тиск у капілярі, і рідина з балону пульверизатора під дією більшого атмосферного тиску піднімається по капіляру. Там вона роздроблюється струменем повітря.

Водоструминний насос

Водоструминний насос – резервуар, у який впаяні дві трубки. Під дією тиску у першу трубку протікає вода, потрапляючи потім у другу трубку. У звуженій частині першої трубки виникає зменшений тиск, який менший за атмосферний. Тому у резервуарі створюється напруження. Трубку приєднують до резервуару, який проходить у посудину, з якої необхідно відкачати повітря.

Карбюратор

Карбюратор – пристрій у системі живлення карбюраторних двигунів внутрішнього згоряння, що застосовується для змішування бензину та повітря. Під час руху поршня у такті впускання тиск у циліндрі знижується. При цьому навколишнє повітря всмоктується циліндром через повітряну трубу карбюратора — дифузор. У найвужчій частині дифузора, де тиск відповідно найменший, розташовано розпилювач, із якого витікає паливо. Паливо подрібнюється струменем повітря на маленькі краплі, і утворюється горюча суміш.

Осушування боліт

Осушування боліт за принципом закону Бернуллі проводилося дуже давно. До болота підводили канали від найближчої річки. Внаслідок великої різниці тисків між водою з болота та водою з каналу вода з каналу “всмоктувала” воду з болота.

Ракета

У конструюванні ракет також застосовується закон Бернуллі. Для створення тяги у ракеті використовується паливо, яке спалюють у камері згоряння. Гази утворюють реактивний струмінь, який прискорюється, коли проходить через спеціальне звуження – сопло. Са́ме звуження сопла і є основною причиною прискорення реактивного струменя газів і збільшення реактивної тяги.

Свисток

Свисток являє собою приклад використання закону Бернуллі у газоструменевих випромінювачах звукових хвиль. Вихровий свисток являє собою циліндричну камеру, у подається потік повітря через тангенціально розташовану трубку. Утворений вихровий потік надходить у вихідну трубку меншого діаметру, яка розташована на осі. Там інтенсивність вихору різко підвищується та тиск в його центрі стає значно нижче атмосферного. Перепад тиску періодично вирівнюється за рахунок прориву газів з атмосфери у вихідну трубку та руйнування вихору.

Диск Релея

Диск Релея – прилад для вимірювання коливальної швидкості частинок у звуковій хвилі та сили звуку. Являє собою тонку пластинку круглої форми, із слюди або металу, підвішену на тонку кварцеву нитку. Зазвичай диск розміщують під кутом у 45º до напряму коливань частинок середовища, оскільки таке розташування найбільш чутливе до коливань. При розповсюдженні звукових хвиль диск повертається перпендикулярно до напряму коливань. Це відбувається через те, що при обтіканні пластинки тиск, згідно із законом Бернуллі більший у тому місці, де швидкість менша. Сили тиску уворюють обертальний момент, який урівноважується за рахунок пружності нитки. При цьому диск встановлюється до напряму потоку під кутом, що більший, ніж 45º. за кутом повороту диску визначають силу звуку. У постійному потоці кут повороту диска Релея пропорційний квадрату швидкості, при звукових коливаннях – квадрату амплітуди швидкості, і цей кут не залежить від частоти.

Неправильне застосування закону Бернуллі

Підіймальна сила літака зумовлюється специфічною будовою крила. Донедавна для пояснення причини підіймальної сили крила застосовували закон Бернуллі. Відповідно до закону Бернуллі, пояснення підіймальної сили літака виглядає так: крило має особливу будову – знизу воно має пряме, а його верхня частина заокруглена. Це дозволяє збільшити площу верхньої частини крила. Згідно із законом Бернуллі, із збільшенням швидкості тиск зменшується. А оскільки повітря долає шлях під крилом та над крилом за однаковий проміжок часу, під крилом виникає область із збільшеним тиском, що зумовлює підйом літака у повітря. Таким чином виникає підйомна сила.
Проте, згідно з сучасними уявленнями, підіймальна сила крила виникає не внаслідок закону Бернуллі. Рух повітряної маси перед крилом можна вважати суцільним, він характеризується одним показником швидкості. Коли повітряна маса контактує з крилом, вона розбивається на дві частини, які, внаслідок форми крила, мають різні швидкості і це зумовлює різний тиск. Однак це не може бути причиною підйомної сили, оскільки ці дві повітряні маси обтікають відповідно верхню і нижню частини крила не за однаковий час, бо, на відміну від колишніх уявлень, ці повітряні потоки не поєднуються на кінці крила. Отже, більша довжина верхньої частини крила не означає більшої швидкості руху повітря. Отже, хоча закон Бернуллі і можна застосувати для повітряних мас, які розсікаються крилом (більша швидкість зумовлює менший тиск), проте він один не пояснює підіймальну силу крила. Для повного пояснення слід застосовувати теорему Жуковського.

Отримано з https://wiki.tntu.edu.ua/index.php?title=Користувач:Valdemar88&oldid=5107