Відмінності між версіями «Нейронні мережі»
Symchak (обговорення • внесок) (→Список використаної літератури) |
Symchak (обговорення • внесок) (→Список використаних джерел) |
||
| Рядок 47: | Рядок 47: | ||
== Список використаних джерел == | == Список використаних джерел == | ||
#http://ru.wikipedia.org/wiki/Алгоритм_Левенберга_—_Марквардта | #http://ru.wikipedia.org/wiki/Алгоритм_Левенберга_—_Марквардта | ||
| − | #http://catalog.gaw.ru/index.php?page=document&id=1438 | + | #http://catalog.gaw.ru/index.php?page=document&id=1438 |
| − | #http://www.ukrreferat.com/index.php?referat=51882 | + | #http://www.ukrreferat.com/index.php?referat=51882 |
#http://www.machinelearning.ru/wiki/index.php?title=Нейронные_сети | #http://www.machinelearning.ru/wiki/index.php?title=Нейронные_сети | ||
Версія за 23:20, 23 лютого 2011
| Презентація доповіді на тему Нейронні мережі. Реалізація в MatLab. є розміщеною в Репозиторії. |
| {{{img}}} | ||
| Імя | Володимир | |
| Прізвище | Симчак | |
| По-батькові | Сергійович | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | СН-10-097 | |
Зміст
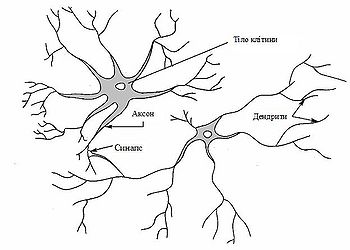
Біологічні нейронні мережі
Нервова система людини побудована з елементів (нейронів), має приголомшуючу складність. Близько 1011 нейронів беруть участь в приблизно 1015 передаючих зв'язках, що мають довжину метр і більше. Кожен нейрон володіє багатьма якостями, спільними з іншими елементами тіла, але його унікальною здатністю є прийом, обробка і передача електрохімічних сигналів по нервових шляхах, які утворюють комунікаційну систему мозку.Дендрити (входи нейрона) йдуть від тіла нервової клітини до інших нейронів, де вони приймають сигнали в точках з'єднання (синапсах). Прийняті синапсом вхідні сигнали підводяться до тіла нейрона. Тут вони підсумовуються, причому одні входи стимулюють активізацію нейрона, а інші – зниження його активності. Коли сумарна активність (збудження) нейрона перевищує деякий поріг, нейрон переходить в активний стан, посилаючи по аксону (виходу нейрона) сигнал іншим нейронам. У цієї основної функціональної схеми багато спрощень і виключень, проте більшість штучних нейронних мереж моделює лише ці прості властивості.
Штучний нейрон
Основними компонентами нейромережі є нейрони /neurons/ (елементи, вузли), які з’єднані зв’язками. Сигнали передаються по зваженим зв’язкам (connection), з кожним з яких пов’язаний ваговий коефіцієнт (weighting coefficient) або вага. Моделі НМ – програмні і апаратні, найбільш поширені – програмні. Використання – розпізнавання образів, прогнозування, створення асоціативної пам’яті. Штучний нейрон імітує в першому наближенні властивості біологічного нейрона. На вхід штучного нейрона поступає множина сигналів, які є виходами інших нейронів. Кожен вхід множиться на відповідну вагу, аналогічну його синаптичній силі, і всі виходи підсумовуються, визначаючи рівень активації нейрона.
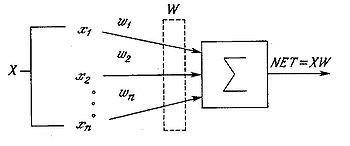
Хоча мережеві парадигми досить різноманітні, в основі майже всіх їх лежить ця конфігурація. Тут множина вхідних сигналів, позначених x1, x2,…, xn, поступає на штучний нейрон. Ці вхідні сигнали, в сукупності позначаються вектором X, відповідають сигналам, що приходять в синапси біологічного нейрона. Кожен сигнал множиться на відповідну вагу w1, w2,…, wn, і поступає на сумуючий блок, позначений Σ. Кожна вага відповідає «силі» одного біологічного синаптичного зв'язку (множина ваг в сукупності позначається вектором W). Сумуючий блок, який відповідає тілу біологічного нейрона, складає зважені входи алгебраїчно, створюючи вихід, який ми називатимемо NET.
Активіаційні функції
Сигнал NET далі, як правило, перетворюється активаційною функцією F і дає вихідний нейронний сигнал OUT = F(NET). Активаційна функція F(NET) може бути:
1. Пороговою бінарною функцією
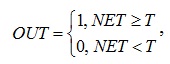
де Т – деяка постійна порогова величина, або ж функція, що точніше моделює нелінійну передавальну характеристику біологічного нейрона.
2. Лінійною обмеженою функцією
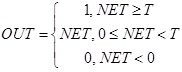
3. Функцією гіперболічного тангенса
![]()
де С > 0 – коефіцієнт ширини сигмоїди по осі абсцис (звичайно С=1).
4. Сигмоїдною (S-подібною) або логістичною функцією
![]()
З виразу для сигмоїда очевидно, що вихідне значення нейрона лежить в діапазоні [0,1]. Популярність сигмоїдної функції зумовлюють наступні її властивості:
- здатність підсилювати слабкі сигнали сильніше, ніж великі, і опиратися “насиченню” від потужних сигналів;
- монотонність і диференційованість на всій осі абсцис;
- простий вираз для похідної, що дає можливість використовувати широкий спектр оптимізаційних алгоритмів.