Відмінності між версіями «Дрейф неоднорідностей»
Shkod (обговорення • внесок) м (Відкинуто редагування Paseka Viktor (обговорення) до зробленого Northfear) |
|||
| (Не показані 17 проміжних версій 5 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name= Ярослав| Surname=Слойка | FatherNAme=|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
| − | + | Презентація доповіді (http://elartu.tstu.edu.ua/handle/123456789/403). | |
= Дрейф неоднорідностей = | = Дрейф неоднорідностей = | ||
| Рядок 10: | Рядок 11: | ||
Навантаження об’єму – це концентрація стружки в соці, точніше маса стружки, що припадає на одиницю об’єму суміші. Навантаження об’єму дифузійного апарата, що складає в середньому 0,4-0,5 кг/дм3, може знижуватися до 0,2-0,3 кг/дм3, або зростати до 0,6-0,7 кг/дм3, причому його зміну не можна пов’язати з плином часу. Тому при проведенні дослідження вирішено вибрати дрейф неоднорідностей за рахунок змін навантаження об’єму, а впливу решти шумових факторів уникнути, проводячи вимірювання теплопровідності в стаціонарному режимі через однаковий проміжок часу з моменту змішування стружки і соку для всіх зразків. | Навантаження об’єму – це концентрація стружки в соці, точніше маса стружки, що припадає на одиницю об’єму суміші. Навантаження об’єму дифузійного апарата, що складає в середньому 0,4-0,5 кг/дм3, може знижуватися до 0,2-0,3 кг/дм3, або зростати до 0,6-0,7 кг/дм3, причому його зміну не можна пов’язати з плином часу. Тому при проведенні дослідження вирішено вибрати дрейф неоднорідностей за рахунок змін навантаження об’єму, а впливу решти шумових факторів уникнути, проводячи вимірювання теплопровідності в стаціонарному режимі через однаковий проміжок часу з моменту змішування стружки і соку для всіх зразків. | ||
Перший основний параметр x1 (середню температуру зразка в стаціонарному режимі) встановлювали регулюванням потужності електронагрівача приладу, другий x2 (концентрацію цукру в соці) обчислювали по вихідній концентрації розчину c %. | Перший основний параметр x1 (середню температуру зразка в стаціонарному режимі) встановлювали регулюванням потужності електронагрівача приладу, другий x2 (концентрацію цукру в соці) обчислювали по вихідній концентрації розчину c %. | ||
| − | <center> '''Розв’язання''' </center> | + | <center> ''' |
| + | == Розв’язання == | ||
| + | ''' </center> | ||
Оскільки метою дослідів було з’ясувати, чи є навантаження об’єму шумовим чи основним фактором, планування було проведене з розрахунку простого дрейфу – ступінчастого. Рівні та інтервали вимірювання основних факторів для ПФЕ 22 наведене в таблиці 1. | Оскільки метою дослідів було з’ясувати, чи є навантаження об’єму шумовим чи основним фактором, планування було проведене з розрахунку простого дрейфу – ступінчастого. Рівні та інтервали вимірювання основних факторів для ПФЕ 22 наведене в таблиці 1. | ||
За правилами ортогональності розбиваємо матрицю планування на два блоки, які є напіврепліками 22-1. Порівнюємо парну взаємодію безрозмірних факторів z1 z2 з новою незалежною змінною, яка характеризує дрейф | За правилами ортогональності розбиваємо матрицю планування на два блоки, які є напіврепліками 22-1. Порівнюємо парну взаємодію безрозмірних факторів z1 z2 з новою незалежною змінною, яка характеризує дрейф | ||
| + | <center> '''z1 z2 = zд''' </center> | ||
| − | |||
Таблиця 1 Вхідні дані для ПФЕ в умовах ступінчастого дрейфу | Таблиця 1 Вхідні дані для ПФЕ в умовах ступінчастого дрейфу | ||
| Рядок 21: | Рядок 24: | ||
| − | У першому блоці проводилися досліди при zд = -1, як нижній рівень навантаження об’єму обрали величину 0,3 кг/дм3 , у 2-му - zд = +1, навантаження об’єму було | + | У першому блоці проводилися досліди при zд = -1, як нижній рівень навантаження об’єму обрали величину 0,3 кг/дм3 , у 2-му - zд = +1, навантаження об’єму було 0,6 кг/дм3. Матриця планування та результати вимірювання вихідної функції y, тобто коефіцієнти теплопровідності λ, Вт/(м*К), наведено в таб. 2 |
| − | |||
Таблиця 2 Матриця ПФЕ для умов ступінчастого дрейфу неоднорідності | Таблиця 2 Матриця ПФЕ для умов ступінчастого дрейфу неоднорідності | ||
| − | + | <center>[[Файл:Tab2.JPG]]</center> | |
| − | + | ||
| − | |||
| − | |||
| − | |||
Для обробки використовувалися рівняння, наведені в п.6,2 [1]. У результаті утворено математичну модель поведінки теплопровідності соко-стружкової суміші в процесі екстракції для безрозмірних факторів | Для обробки використовувалися рівняння, наведені в п.6,2 [1]. У результаті утворено математичну модель поведінки теплопровідності соко-стружкової суміші в процесі екстракції для безрозмірних факторів | ||
| − | y = 0.480 – 0.043* z1 + 0.026*z2 | + | <center> y = 0.480 – 0.043* z1 + 0.026*z2 </center> |
| + | |||
Перехід до вимірних параметрів проведено за допомогою звичайних способів | Перехід до вимірних параметрів проведено за допомогою звичайних способів | ||
| − | λ = 0,770 – 0,006*t + 0.008*c | + | |
| + | <center> λ = 0,770 – 0,006*t + 0.008*c </center> | ||
Таким чином, утворено залежність для λ тільки від основних факторів, виключивши вплив навантаження об’єму. Зазначимо, що звільнившись від впливу дрейфу (часового або неоднорідностей) можна оцінити його і вирішити, чи немає потреби перевести який-небудь із шумових факторів в основні. Для цього треба розрахувати коефіцієнт при zд за формулою. | Таким чином, утворено залежність для λ тільки від основних факторів, виключивши вплив навантаження об’єму. Зазначимо, що звільнившись від впливу дрейфу (часового або неоднорідностей) можна оцінити його і вирішити, чи немає потреби перевести який-небудь із шумових факторів в основні. Для цього треба розрахувати коефіцієнт при zд за формулою. | ||
| − | + | <center>[[Файл:formul1.JPG]]</center> | |
У нашому прикладі | У нашому прикладі | ||
| − | + | <center>[[Файл:formul2.JPG]]</center> | |
Потім треба розрахувати y для обох блоків у центрі плану експерименту. | Потім треба розрахувати y для обох блоків у центрі плану експерименту. | ||
Різниця між значеннями y для обох блоків дає оцінку зміни функції відклику. Розрахунки для прикладу λ за 1-м блоком: | Різниця між значеннями y для обох блоків дає оцінку зміни функції відклику. Розрахунки для прикладу λ за 1-м блоком: | ||
| − | y1 = 0,48 − 0,023 = 0,457 Вт/(м∙К) | + | <center>y1 = 0,48 − 0,023 = 0,457 Вт/(м∙К)</center> |
за 1-м блоком: | за 1-м блоком: | ||
| − | y2 = 0,48 + 0,023 = 0,503 Вт/(м∙К) | + | <center>y2 = 0,48 + 0,023 = 0,503 Вт/(м∙К)</center> |
Загальний дрейф функції відклику в результаті збільшення навантаження об’єму з 0,3 до 0,6 кг/м3 такий: | Загальний дрейф функції відклику в результаті збільшення навантаження об’єму з 0,3 до 0,6 кг/м3 такий: | ||
| − | ∆y = 0,503 – 0,457 = 0,046 Вт/(м∙К) | + | <center>∆y = 0,503 – 0,457 = 0,046 Вт/(м∙К)</center> |
Отже функція відклику змінилася на 10% при цілком реальній у виробничих умовах зміні навантаження об’єму. | Отже функція відклику змінилася на 10% при цілком реальній у виробничих умовах зміні навантаження об’єму. | ||
Аналіз утворених результатів показав, що цей вплив зіставлюваний з впливом незалежних змінних t і c , тому в подальшому при дослідженнях треба перейти від двофакторних до трифакторних експериментів. | Аналіз утворених результатів показав, що цей вплив зіставлюваний з впливом незалежних змінних t і c , тому в подальшому при дослідженнях треба перейти від двофакторних до трифакторних експериментів. | ||
| + | |||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 16:36, 17 грудня 2019
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Ярослав | |
| Прізвище | Слойка | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
Презентація доповіді (http://elartu.tstu.edu.ua/handle/123456789/403).
Дрейф неоднорідностей
Наведемо результати досліджень теплофізичних характеристик соко-стружкової суміші дифузійних апаратів цукрової промисловості. Відомо, що на коефіцієнт теплопровідності λ цукрових розчинів, в основному, впливають концентрація цукру і температура розчину. На ефективну теплопровідність соко-стружкової суміші впливають також численні фактори, які при проведенні експериментів спотворюватимуть вплив основних факторів. Серед них до часового дрейфу належить наявність на поверхні стружки адсорбованого повітря, кількість якого змінюватиметься в процесі контакту соку і стружки, а також зміна концентрації цукру в стружці в процесі дифузії. Проте серед факторів є один, який до часового дрейфу не належить. Це ступінь неоднорідності суміші або, як називають його виробничники, навантаження об’єму.
Навантаження об’єму – це концентрація стружки в соці, точніше маса стружки, що припадає на одиницю об’єму суміші. Навантаження об’єму дифузійного апарата, що складає в середньому 0,4-0,5 кг/дм3, може знижуватися до 0,2-0,3 кг/дм3, або зростати до 0,6-0,7 кг/дм3, причому його зміну не можна пов’язати з плином часу. Тому при проведенні дослідження вирішено вибрати дрейф неоднорідностей за рахунок змін навантаження об’єму, а впливу решти шумових факторів уникнути, проводячи вимірювання теплопровідності в стаціонарному режимі через однаковий проміжок часу з моменту змішування стружки і соку для всіх зразків. Перший основний параметр x1 (середню температуру зразка в стаціонарному режимі) встановлювали регулюванням потужності електронагрівача приладу, другий x2 (концентрацію цукру в соці) обчислювали по вихідній концентрації розчину c %.
Розв’язання
Оскільки метою дослідів було з’ясувати, чи є навантаження об’єму шумовим чи основним фактором, планування було проведене з розрахунку простого дрейфу – ступінчастого. Рівні та інтервали вимірювання основних факторів для ПФЕ 22 наведене в таблиці 1. За правилами ортогональності розбиваємо матрицю планування на два блоки, які є напіврепліками 22-1. Порівнюємо парну взаємодію безрозмірних факторів z1 z2 з новою незалежною змінною, яка характеризує дрейф
Таблиця 1 Вхідні дані для ПФЕ в умовах ступінчастого дрейфу

У першому блоці проводилися досліди при zд = -1, як нижній рівень навантаження об’єму обрали величину 0,3 кг/дм3 , у 2-му - zд = +1, навантаження об’єму було 0,6 кг/дм3. Матриця планування та результати вимірювання вихідної функції y, тобто коефіцієнти теплопровідності λ, Вт/(м*К), наведено в таб. 2
Таблиця 2 Матриця ПФЕ для умов ступінчастого дрейфу неоднорідності
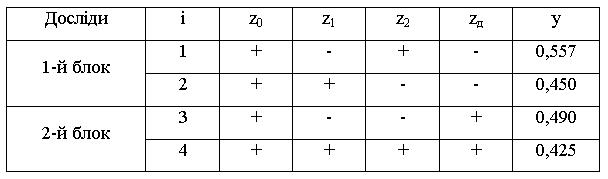
Для обробки використовувалися рівняння, наведені в п.6,2 [1]. У результаті утворено математичну модель поведінки теплопровідності соко-стружкової суміші в процесі екстракції для безрозмірних факторів
Перехід до вимірних параметрів проведено за допомогою звичайних способів
Таким чином, утворено залежність для λ тільки від основних факторів, виключивши вплив навантаження об’єму. Зазначимо, що звільнившись від впливу дрейфу (часового або неоднорідностей) можна оцінити його і вирішити, чи немає потреби перевести який-небудь із шумових факторів в основні. Для цього треба розрахувати коефіцієнт при zд за формулою.
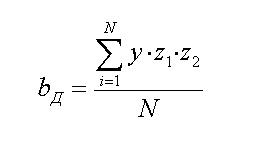
У нашому прикладі
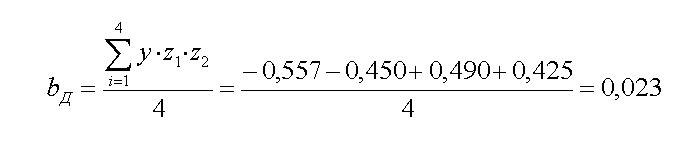
Потім треба розрахувати y для обох блоків у центрі плану експерименту. Різниця між значеннями y для обох блоків дає оцінку зміни функції відклику. Розрахунки для прикладу λ за 1-м блоком:
за 1-м блоком:
Загальний дрейф функції відклику в результаті збільшення навантаження об’єму з 0,3 до 0,6 кг/м3 такий:
Отже функція відклику змінилася на 10% при цілком реальній у виробничих умовах зміні навантаження об’єму. Аналіз утворених результатів показав, що цей вплив зіставлюваний з впливом незалежних змінних t і c , тому в подальшому при дослідженнях треба перейти від двофакторних до трифакторних експериментів.