Відмінності між версіями «Фонтан Герона»
Наталя (обговорення • внесок) |
Наталя (обговорення • внесок) |
||
| (Не показано 5 проміжних версій цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | '''Фонтан Герона''' - придуманий Героном Олександрійським дотепний прилад, який служить одним із зразків знань древніх греків(за 200 років до н. Е..) В галузі гідростатики і аеростатики. | + | '''Фонтан Герона''' - придуманий Героном Олександрійським дотепний прилад, який служить одним із зразків знань древніх греків (за 200 років до н. Е..) В галузі гідростатики і аеростатики. Це фонтан, який працює без енергетичних затрат. |
| + | |||
| + | == Принцип дії та схема фонтану Герона == | ||
| + | |||
| + | [[Файл:схема фонтану Герона.jpg|200px|thumb|right|рис.1]] | ||
| + | |||
| + | Фонтан складається з трьох частин: чашка А з фонтанною трубкою, а також дві посудини В і С які частково заповнені водою. Посудини з'єднані з двома гнучкими трубками як показано на рис.1: чашка A з більш низькою посудиною С і ємність C з вищою посудиною В. Посудина B з чашкою може бути розміщена на стільці, а інша нижче рівня стільця. Чаша А підтримується вище посудини B і з'єднана з нижньою посудиною C за допомогою гнучкого шланга. | ||
| + | Спочатку тиск в обох посудинах, B і C, рівний атмосферному тиску. Якщо заповнити чашку А водою, то вода з чашки A стікатиме в нижню посудину С, яка містить повітря і виробляє додатковий гідростатичний тиск | ||
| + | |||
| + | |||
| + | <math> P_2 = \rho\ g h_2 </math> , | ||
| + | |||
| + | |||
| + | де <math> \rho\ </math> - густина води. | ||
| + | |||
| + | |||
| + | [[Файл:фонтан Герона.png|200px|thumb|right|рис.2]] | ||
| + | |||
| + | [[Файл:Heron's_Fountain.png|200px|thumb|right|рис.3]] | ||
| + | |||
| + | За Паскалем цей додатковий тиск передається незмінним в усіх напрямках, а отже, і повітрю всередині посудини С. В результаті цього під дією тиску повітря переміщається з посудини C до верхньої посудини B. Витиснуте повітря з нижньої посудини C стискає повітря у верхній посудині B і змушує воду з фонтану переміщатись вверх по трубці. У цей момент гідростатичний тиск у верху посудини B дорівнює | ||
| − | |||
| − | |||
| − | |||
<math>P_1 = \rho\ g h_1 </math> | <math>P_1 = \rho\ g h_1 </math> | ||
| − | |||
| − | <math> \ | + | Отже, тиск води у фонтані є різницею гідростатичного тису у посудинах C і В. Тому |
| + | |||
| + | |||
| + | <math> \Delta\ P = P_2-P_1 = \rho\ g h_2 - \rho\ g h_1 = \rho\ g (h_2-h_1)\qquad(1)</math> | ||
| + | |||
| − | Іншими словами тиск <math> \ | + | Іншими словами тиск <math> \Delta\ P </math> стискає повітря у верхній посудині B і приводить в дію фонтан. |
| − | Якщо знехтувати висотою сопла над рівнем води в чашці А,перепад висоти <math> h_2 - h_1 </math> буде дорівнювати висоті рівня води у чашці А, виміряної по відношенню до рівня води в посудині С. Змінюючи цю висоту ми можемо підтримувати фонтан. | + | Якщо знехтувати висотою сопла над рівнем води в чашці А, перепад висоти <math> h_2 - h_1 </math> буде дорівнювати висоті рівня води у чашці А, виміряної по відношенню до рівня води в посудині С. Змінюючи цю висоту ми можемо підтримувати фонтан. |
Фонтан Герона є також гарним прикладом для демонстрації принципу Бернуллі. Принцип Бернуллі є результатом застосування теореми «Енергії роботи в одиниці об'єму рідини, що рухається». | Фонтан Герона є також гарним прикладом для демонстрації принципу Бернуллі. Принцип Бернуллі є результатом застосування теореми «Енергії роботи в одиниці об'єму рідини, що рухається». | ||
| − | Він стверджує , що робота на одиницю об'єму рідини з боку зовнішньої рідини дорівнює сумі змін кінетичної і потенціальної енергії на одиницю об'єму , які відбуваються під час потоку. | + | Він стверджує, що робота на одиницю об'єму рідини з боку зовнішньої рідини дорівнює сумі змін кінетичної і потенціальної енергії на одиницю об'єму, які відбуваються під час потоку. |
| − | Застосуємо принцип Бернуллі для води в резервуарі А і | + | Застосуємо принцип Бернуллі для води в резервуарі А і потоку води з сопла. Потенціальна енергія одиниці об'єму води на рівні резервуару А і сопла відповідно: <math> \rho\ g h_2 </math> і <math> \rho\ g h_1 </math> , і кінетичні енергії відповідно 0 і <math> \frac{\rho\ v^2}{2} </math> |
| − | Таким чином з рівняння Бернуллі: | + | Таким чином з рівняння Бернуллі: |
| − | + | ||
| − | + | ||
| − | де | + | <math> P_{atm} + \frac{\rho\ v^2}{2} + \rho\ g h_1 = P_{atm} + \rho\ g h_2 \qquad(2)</math> |
| − | + | ||
| − | + | ||
| − | В отриманому рівнянні(3) припущено, що наявне повітря є нестисливе, тому нехтуємо тертям. Звичайно, реальна швидкість води з сопла буде меншою, ніж це | + | де <math> P_{atm} </math> - атмосферний тиск. |
| − | + | ||
| + | |||
| + | Швидкість потоку води з сопла фонтану трубки може бути легко знайдена з рівнянь (1) і (2) як: | ||
| + | |||
| + | |||
| + | <math> v = \sqrt{2g (h_2 - h_1)} = \sqrt{\frac{2\Delta P}{\rho}} \qquad(3)</math> | ||
| + | |||
| + | |||
| + | В отриманому рівнянні(3) припущено, що наявне повітря є нестисливе, тому нехтуємо тертям. Звичайно, реальна швидкість води з сопла буде меншою, ніж це визначається рівнянням (3). Розглянемо знову рідини в ідеальному русі з посудини C вгору і вниз, ми можемо змінити надлишковий тиск <math> \Delta\ P </math>, і в результаті швидкість води з сопла буде змінюватися. | ||
| + | Якщо тиск <math> \Delta\ P </math> збільшиться, то швидкість води теж збільшиться і вода підніматиметься все вище по відношенню до сопла, створюючи фонтанний ефект. Якщо посудина C знизиться ще більше, то гідростатичний тиск зросте всередині посудини C, а отже і всередині посудини B, в результаті цього фонтан підніметься ще вище. І навпаки, якщо посудина C піднімається відносно посудини B, гідростатичний тиск зменшується, і бризки фонтану зменшується. | ||
| + | |||
| + | |||
| + | Як ви розумієте, час роботи подібних фонтанів не є нескінченним, зрештою вся вода з середньої посудини, перетече в нижню і фонтан перестане працювати. | ||
| + | |||
| + | == Застосування == | ||
| + | |||
| + | [[Файл:Рис_5.PNG|200px|thumb|right|рис.4]] | ||
| + | [[Файл:Рис_6.PNG|200px|thumb|right|рис.5]] | ||
| + | |||
| + | Використовуючи принцип фонтану Герона, можна створювати високопродуктивні насосні установки неперервної дії , які зможуть піднімати | ||
| + | воду на висоту кількох метрів, не витрачаючи при цьому ні грама вугілля або бензину , ні ватта електричної енергії. Як це можна здійснити, наочно показано иа рис.4. Упоперек річки встановлена гребля, верхній край якої трохи нижчий за рівень води. Вода, переливаючись через край, падає на ротор, зібраний з декількох великих бочок, які з'єднані трубками і обертає його. Але можна обійтися і без греблі , якщо цей самий ротор, як показано на рис.5, буде обертатися на валі в притоплену стані. Система з послідовно з'єднаних між собою бочок буде по черзі забирати всередину то повітря, то воду і піднімати її. Так дармова енергія течії річки зможе без проміжних перетворювачів подавати воду для поливу садів і городів, живити зрошувальні системи , використовуватися для інших потреб. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Література == | ||
| + | # Bennet Woodcroft, The Pneumatics of Hero of Alexandria, London, 1851. | ||
| + | # Freier and Anderson, A Demonstration Handbook for Physics. | ||
| + | # Perelman, Y., "Physics Can Be Fun" (Mir Publishers, English version 1975), Perelman, Y. "Modification of Heron's Fountain," Physics Can be Fun, pp. 300-303. | ||
| + | # Thomas B. Greenslade, Jr., "Nineteenth Century Textbook Illustrations, XLI. Hero's Fountain", Phys. Teach. 20, 169-70 (1982). | ||
| − | + | == Посилання == | |
| + | # [http://www.galileo-tv.ru/node/4087 Эксперимент. Фонтан Герона] | ||
Поточна версія на 16:38, 25 грудня 2013
Фонтан Герона - придуманий Героном Олександрійським дотепний прилад, який служить одним із зразків знань древніх греків (за 200 років до н. Е..) В галузі гідростатики і аеростатики. Це фонтан, який працює без енергетичних затрат.
Принцип дії та схема фонтану Герона
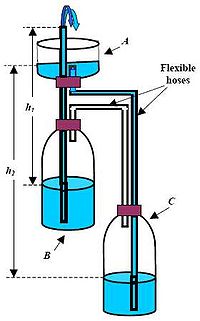
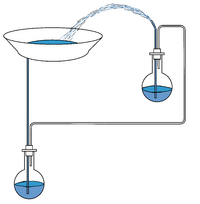
Фонтан складається з трьох частин: чашка А з фонтанною трубкою, а також дві посудини В і С які частково заповнені водою. Посудини з'єднані з двома гнучкими трубками як показано на рис.1: чашка A з більш низькою посудиною С і ємність C з вищою посудиною В. Посудина B з чашкою може бути розміщена на стільці, а інша нижче рівня стільця. Чаша А підтримується вище посудини B і з'єднана з нижньою посудиною C за допомогою гнучкого шланга. Спочатку тиск в обох посудинах, B і C, рівний атмосферному тиску. Якщо заповнити чашку А водою, то вода з чашки A стікатиме в нижню посудину С, яка містить повітря і виробляє додатковий гідростатичний тиск
[math]P_2 = \rho\ g h_2[/math] ,
де [math]\rho\[/math] - густина води.
За Паскалем цей додатковий тиск передається незмінним в усіх напрямках, а отже, і повітрю всередині посудини С. В результаті цього під дією тиску повітря переміщається з посудини C до верхньої посудини B. Витиснуте повітря з нижньої посудини C стискає повітря у верхній посудині B і змушує воду з фонтану переміщатись вверх по трубці. У цей момент гідростатичний тиск у верху посудини B дорівнює
[math]P_1 = \rho\ g h_1[/math]
Отже, тиск води у фонтані є різницею гідростатичного тису у посудинах C і В. Тому
[math]\Delta\ P = P_2-P_1 = \rho\ g h_2 - \rho\ g h_1 = \rho\ g (h_2-h_1)\qquad(1)[/math]
Іншими словами тиск [math]\Delta\ P[/math] стискає повітря у верхній посудині B і приводить в дію фонтан.
Якщо знехтувати висотою сопла над рівнем води в чашці А, перепад висоти [math]h_2 - h_1[/math] буде дорівнювати висоті рівня води у чашці А, виміряної по відношенню до рівня води в посудині С. Змінюючи цю висоту ми можемо підтримувати фонтан.
Фонтан Герона є також гарним прикладом для демонстрації принципу Бернуллі. Принцип Бернуллі є результатом застосування теореми «Енергії роботи в одиниці об'єму рідини, що рухається».
Він стверджує, що робота на одиницю об'єму рідини з боку зовнішньої рідини дорівнює сумі змін кінетичної і потенціальної енергії на одиницю об'єму, які відбуваються під час потоку.
Застосуємо принцип Бернуллі для води в резервуарі А і потоку води з сопла. Потенціальна енергія одиниці об'єму води на рівні резервуару А і сопла відповідно: [math]\rho\ g h_2[/math] і [math]\rho\ g h_1[/math] , і кінетичні енергії відповідно 0 і [math]\frac{\rho\ v^2}{2}[/math]
Таким чином з рівняння Бернуллі:
[math]P_{atm} + \frac{\rho\ v^2}{2} + \rho\ g h_1 = P_{atm} + \rho\ g h_2 \qquad(2)[/math]
де [math]P_{atm}[/math] - атмосферний тиск.
Швидкість потоку води з сопла фонтану трубки може бути легко знайдена з рівнянь (1) і (2) як:
[math]v = \sqrt{2g (h_2 - h_1)} = \sqrt{\frac{2\Delta P}{\rho}} \qquad(3)[/math]
В отриманому рівнянні(3) припущено, що наявне повітря є нестисливе, тому нехтуємо тертям. Звичайно, реальна швидкість води з сопла буде меншою, ніж це визначається рівнянням (3). Розглянемо знову рідини в ідеальному русі з посудини C вгору і вниз, ми можемо змінити надлишковий тиск [math]\Delta\ P[/math], і в результаті швидкість води з сопла буде змінюватися.
Якщо тиск [math]\Delta\ P[/math] збільшиться, то швидкість води теж збільшиться і вода підніматиметься все вище по відношенню до сопла, створюючи фонтанний ефект. Якщо посудина C знизиться ще більше, то гідростатичний тиск зросте всередині посудини C, а отже і всередині посудини B, в результаті цього фонтан підніметься ще вище. І навпаки, якщо посудина C піднімається відносно посудини B, гідростатичний тиск зменшується, і бризки фонтану зменшується.
Як ви розумієте, час роботи подібних фонтанів не є нескінченним, зрештою вся вода з середньої посудини, перетече в нижню і фонтан перестане працювати.
Застосування
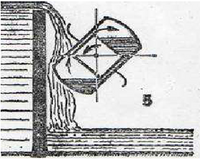
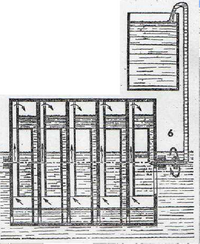
Використовуючи принцип фонтану Герона, можна створювати високопродуктивні насосні установки неперервної дії , які зможуть піднімати воду на висоту кількох метрів, не витрачаючи при цьому ні грама вугілля або бензину , ні ватта електричної енергії. Як це можна здійснити, наочно показано иа рис.4. Упоперек річки встановлена гребля, верхній край якої трохи нижчий за рівень води. Вода, переливаючись через край, падає на ротор, зібраний з декількох великих бочок, які з'єднані трубками і обертає його. Але можна обійтися і без греблі , якщо цей самий ротор, як показано на рис.5, буде обертатися на валі в притоплену стані. Система з послідовно з'єднаних між собою бочок буде по черзі забирати всередину то повітря, то воду і піднімати її. Так дармова енергія течії річки зможе без проміжних перетворювачів подавати воду для поливу садів і городів, живити зрошувальні системи , використовуватися для інших потреб.
Література
- Bennet Woodcroft, The Pneumatics of Hero of Alexandria, London, 1851.
- Freier and Anderson, A Demonstration Handbook for Physics.
- Perelman, Y., "Physics Can Be Fun" (Mir Publishers, English version 1975), Perelman, Y. "Modification of Heron's Fountain," Physics Can be Fun, pp. 300-303.
- Thomas B. Greenslade, Jr., "Nineteenth Century Textbook Illustrations, XLI. Hero's Fountain", Phys. Teach. 20, 169-70 (1982).