Відмінності між версіями «Реактивне сопло»
Taras (обговорення • внесок) |
Taras (обговорення • внесок) (→Принцип дії) |
||
| (Не показано 29 проміжних версій цього користувача) | |||
| Рядок 4: | Рядок 4: | ||
Сопло являє собою канал, звужений в середині. У простому випадку таке сопло може складатися з пари усічених конусів, сполучених вузькими кінцями. Ефективні сопла сучасних ракетних двигунів профілюються на підставі газодинамічних розрахунків. | Сопло являє собою канал, звужений в середині. У простому випадку таке сопло може складатися з пари усічених конусів, сполучених вузькими кінцями. Ефективні сопла сучасних ракетних двигунів профілюються на підставі газодинамічних розрахунків. | ||
Пріоритет Годдарда на застосування сопла Лаваля для ракет підтверджується малюнком в описі винаходу в патенті США "US Patet 1102653" від 7 липня 1914 р., на двоступеневу твердопаливну ракету, заявленому в жовтні 1913 р. | Пріоритет Годдарда на застосування сопла Лаваля для ракет підтверджується малюнком в описі винаходу в патенті США "US Patet 1102653" від 7 липня 1914 р., на двоступеневу твердопаливну ракету, заявленому в жовтні 1913 р. | ||
| − | У Росії в ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні використовувалось сопло Лаваля, а з корпусом був зв'язаний кільцевий стабілізатор. | + | У Росії в ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні використовувалось сопло Лаваля, а з корпусом був зв'язаний кільцевий стабілізатор. |
У реактивному двигуні застосовують: | У реактивному двигуні застосовують: | ||
* звужуюче реактивне сопло для створення дозвукових швидкостей; | * звужуюче реактивне сопло для створення дозвукових швидкостей; | ||
| Рядок 21: | Рядок 21: | ||
* Масова витрата газу однакова у всіх поперечних перерізах потоку. | * Масова витрата газу однакова у всіх поперечних перерізах потоку. | ||
* Вплив всіх зовнішніх сил і полів (в тому числі гравітаційного) дуже мале. | * Вплив всіх зовнішніх сил і полів (в тому числі гравітаційного) дуже мале. | ||
| − | * Вісь симетрії сопла є просторовою координатою, x. | + | * Вісь симетрії сопла є просторовою координатою '''<math>\, x </math>'''. |
| + | |||
| + | Відношення локальної швидкості '''<math>\,v</math>''' до локальної швидкості звуку '''<math>\, C </math>''' позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати '''<math>\, x </math>''': | ||
| + | <center><math>M = \frac{v}{C}</math> '''(1)'''</center> | ||
| + | |||
| + | З рівняння стану ідеального газу:<math>\frac{dp}{d\rho}=C^2</math>, тут <math>\,\rho</math> - локальна щільність газу, <math>\, p </math> - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера приймає вигляд: | ||
| + | |||
| + | <center><math> | ||
| + | v\frac{dv}{dx} | ||
| + | = - \frac{1}{\rho}\cdot \frac{dp}{dx} | ||
| + | = - \frac{1}{\rho}\cdot \frac{dp}{d\rho}\cdot \frac{d\rho}{dx} | ||
| + | = - \frac{C^2}{\rho}\cdot \frac{d\rho}{dx} | ||
| + | </math>,</center> | ||
| + | |||
| + | якщо врхувати рівняння (1), то отримаємо: | ||
| + | |||
| + | <center><math>\frac{1}{\rho}\cdot \frac{d\rho}{dx} = -M^2\cdot \frac{1}{v}\cdot \frac{dv}{dx}</math>. '''(2)'''</center> | ||
| + | |||
| + | '''Рівняння (2) є ключовим''' <br /> | ||
| + | Переглянемо його в наступній формі: <br /> | ||
| + | <center><math>\frac{1}{\rho} \frac{d\rho}{dx} / \frac{1}{v} \frac{dv}{dx} = -M^2 </math> '''(2.1)'''</center><br /> | ||
| + | Велмчмнм <math>\frac{1}{\rho} \frac{d\rho}{dx} </math> і <math>\frac{1}{v} \frac{dv}{dx} </math> характеризують відносну ступінь змінності по координаті <math> \, x </math> щільності газу і його швидкості відповідно. Причому рівняння (2.1) показує, що співвідношення між цими величинами дорівнює квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність зменшується). Таким чином, на дозвукових швидкостях <math> \, (M <1) </math> щільність змінюється у меншій мірі, ніж швидкість, а на надзвукових <math> \, (M> 1) </math> - навпаки. Як буде видно далі, це і визначає звужуючо-розширюючу форму сопла. | ||
| + | |||
| + | Оскільки масовий розхід газу постіний: | ||
| + | |||
| + | <center><math>\rho\cdot v\cdot A = \mathsf{const}</math>,</center> | ||
| + | где <math>\, A </math> — площа поперечного перерізу сопла, | ||
| + | |||
| + | <center><math>\ln \rho + \ln v + \ln A = \ln(\mathsf{const})</math>,</center> | ||
| + | |||
| + | диференціюючи обидві частини цього рівняння по <math>\, x </math>, отримуємо: | ||
| + | |||
| + | <center><math>\frac{1}{\rho}\cdot \frac{d\rho}{dx} + \frac{1}{v}\cdot \frac{dv}{dx} + \frac{1}{A}\cdot \frac{dA}{dx} = 0</math></center>. | ||
| + | |||
| + | Післяпідстановки з (2) в це рівняння, остаточно отримуємо: | ||
| + | |||
| + | <center><math>\frac{dA}{dx} = \frac{A}{v}\cdot\frac{dv}{dx}\cdot ({M^2 - 1})</math> '''(3)'''</center> | ||
| + | |||
| + | При збільшенні швидкості газу в соплі знак фиразу <math>\frac{A}{v}\cdot\frac{dv}{dx}</math> додатній і, знак похідниї <math>\frac{dA}{dx}</math> визначається знаком виразу: <math>\,({M^2 - 1})</math> | ||
| + | |||
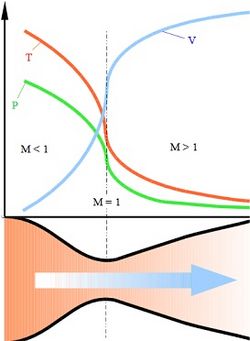
| + | [[Файл:Nozzle de Laval diagram.jpg|thumb|right|250px|Ілюстрація роботи сопла Лаваля. По мірі руху газу по соплу, його абсолютна температура Т і тиск Р понижуються, а швидкість V збільшується. М — число Маха.]] | ||
| + | '''З чого можна зробити наступні висновки:''' | ||
| + | |||
| + | |||
| + | * При '''дозвуковій швидкості''' рух газу <math>\,(M<1)</math>, похідна <math>\frac{dA}{dx}<0</math> ''' — сопло звужується'''. | ||
| + | * При '''надзвуковій швидкості''' рух газу <math>\,(M>1)</math>, похідна <math>\frac{dA}{dx}>0</math> ''' — сопло розширюється'''. | ||
| + | * При русі газу '''зі швидкістю звуку''' <math>\,(M = 1)</math>, похідна <math>\frac{dA}{dx}=0</math> — площа поперечного перерізу досягає '''екстремума''', тобто має місце '''найвужчий переріз''' сопла, яке називається '''критичним'''. | ||
| + | |||
| + | Отже, на звужуючій, докритичній ділянці сопла рух газу відбувається з дозвуковими швидкостями. У найвужчому, критичному перетині сопла локальна швидкість газу досягає звуковій. На розширюючих, закритичних ділянках, газовий потік рухається з надзвуковими швидкостями. | ||
| + | Переміщаючись по соплу, газ розширюється, його температура і тиск падають, а швидкість зростає. Внутрішня енергія газу перетворюється в кінетичну енергію його спрямованого руху. ККД цього перетворення в деяких випадках (наприклад, в соплах сучасних ракетних двигунів) може перевищувати 70%, що значно перевершує ККД реальних теплових двигунів всіх інших типів. Це пояснюється тим, що робоче тіло не передає механічну енергію ніякому посереднику (поршню або лопатям турбіни). В інших теплових двигунах на цій передачі зазнаються значні втрати. Крім того, газ, проходячи через сопло на значній швидкості, не встигає передати його стінкам певну кількість своєї теплової енергії, що дозволяє вважати процес адіабатним. У реальних теплових двигунів інших типів нагрів конструкції становить істотну частину втрат. Автомобільний двигун, наприклад, працює більше на радіатор охолодження, ніж на вихідний вал. | ||
| + | |||
| + | == Швидкість виходу газу із сопла == | ||
| + | З рівняння стану ідеального газу рівняння стану ідеального газу, і Закон збереження енергії | балансу енергії в газовому потоці виводиться формула розрахунку лінійної швидкості витікання газу з сопла Лаваля: | ||
| + | |||
| + | <center><math>v_e = \sqrt{\;\frac{T\;R}{M}\cdot\frac{2\;k}{k-1}\cdot\bigg[ 1-\bigg(\frac {p_e} {p}\bigg)^{(k-1)/k}\bigg]} </math> '''(4)'''</center> | ||
| + | |||
| + | де: | ||
| + | |||
| + | <math>\,v_e</math> — Швидкість газу на виході із сопла, м/с, | ||
| + | |||
| + | <math>\,T</math> — Абсолютна температура газу на вході, | ||
| + | |||
| + | <math>\,R</math> — Универсальна газова стала <math>\,R=8314,5</math> Дж/(кіломоль·К), | ||
| + | |||
| + | <math>\,M</math> — молярна маса газу, кг/кіломоль, | ||
| + | |||
| + | <math>\,k</math> — Показник адіабати <math>\,k=c_p/c_v</math>, | ||
| + | |||
| + | <math>\,c_p</math> — Питома теплоємність при при постійному тиску, Дж/(кіломоль·К), | ||
| + | |||
| + | <math>\,c_v</math> — Удельная теплоёмкость при постоянном объеме, Дж/(кіломоль·К), | ||
| + | |||
| + | <math>\,p_e</math> — Абсолютний тиск газу на виході із сопла, Па | ||
| + | |||
| + | <math>\,p</math> — Абсолютний тиск газу на вході в сопло, Па | ||
| + | |||
| + | == Перспективи == | ||
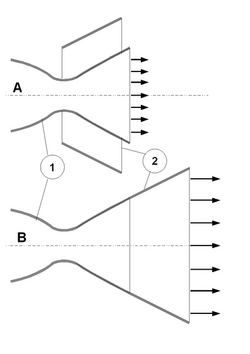
| + | [[Файл:424px-Variable extension nozzle.png|right|250px|thumb|Регулювання степені розширення сопла з насадкою. <br />1 — собственно сопло Лаваля; <br />2 — соплова насадка; <br />А — положення насадки при роботі в нижніх, найбільш щільних, слоях атмосфери; <br />В — положення насадки на великій висоті.]] | ||
| + | Прагнення досягти ефективної роботи двигуна як на Землі, так і на висоті змушує конструкторів шукати технічні рішення, що дозволяють досягти цю мету. Одним з таких рішень з'явився рухливий сопловий насадок - «продовження» сопла, яке пристиковується до нього по досягненні ракетою розріджених шарів атмосфери, збільшуючи, таким чином, ступінь розширення сопла. Схема дії насадки зображена на малюнку справа. Ця схема була практично реалізована, зокрема, в конструкції двигуна [http://uk.wikipedia.org/wiki/%D0%9D%D0%9A-33 НК-33-1]. | ||
| + | |||
| + | [[Файл:800px-F-15_Eagle_Nozzles.jpg|thumb|250px|Регулюючі сопла винищувача F-15]] | ||
| + | Регульовані сопла винищувача F-15 | ||
| + | Проблема оптимізації ступеня розширення сопла дуже актуальна і при розробці авіаційних реактивних двигунів, оскільки літак призначений для польотів в широкому діапазоні висот, а від питомої імпульсу його двигунів в сильній мірі залежить економічність і, отже, дальність польоту. У сучасних турбореактивних двигунах застосовуються регульовані сопла Лаваля. Такі сопла складаються з поздовжніх пластин, що мають можливість переміщення одна відносно одної, зі спеціальним механізмом з гідравлічним або пневматичним приводом, що дозволяє в польоті змінювати площу вихідного і / або критичного перетинів, і, таким чином, домагатися оптимального ступеня розширення сопла при польоті на будь-якій висоті. Регулювання площі прохідних перерізів виконується, як правило, автоматично спеціальною системою управління. Цей же механізм дозволяє по команді пілота змінювати в деяких межах і напрямок реактивного струменя, а отже, напрямок вектора тяги, що істотно підвищує маневреність літака. | ||
| + | |||
| + | |||
| + | |||
| + | <h2>Список використаної літератури</h2> | ||
| + | |||
| + | |||
| + | * Ландау Л. Д., Ліфшиц Е. М. Розділ X. Одновимірний рух газу. § 97. Витік газу із сопла // Теоретична фізика. — Т. 6. Гідродинаміка. | ||
| + | * Моравський А. В., Файн М. А. Як винаходять теплові двигуни. — М.: Знання, 1990. — 192 с. — (Життя чудових ідей). — 50 000 екз. | ||
Поточна версія на 19:45, 9 грудня 2012
Сопло Лаваля - технічне пристосування, яке розганяє газовий потік до надзвукових швидкостей. Широко використовується на деяких типах парових турбін і є важливою частиною сучасних ракетних двигунів і надзвукових реактивних авіаційних двигунів. Сопло являє собою канал, звужений в середині. У простому випадку таке сопло може складатися з пари усічених конусів, сполучених вузькими кінцями. Ефективні сопла сучасних ракетних двигунів профілюються на підставі газодинамічних розрахунків. Пріоритет Годдарда на застосування сопла Лаваля для ракет підтверджується малюнком в описі винаходу в патенті США "US Patet 1102653" від 7 липня 1914 р., на двоступеневу твердопаливну ракету, заявленому в жовтні 1913 р. У Росії в ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні використовувалось сопло Лаваля, а з корпусом був зв'язаний кільцевий стабілізатор. У реактивному двигуні застосовують:
- звужуюче реактивне сопло для створення дозвукових швидкостей;
- звужуюче-розширяюче реактивне сопло (сопло Лаваля) - для отримання надзвукових швидкостей .
- косе сопло - для отримання надзвукових швидкостей при постійному профілі і широкому діапазоні робочих швидкостей.
Принцип дії
Феномен прискорення газу до надзвукових швидкостей в соплі Лаваля був виявлений в кінці XIX ст. експериментальним шляхом. Пізніше це явище знайшло теоретичне пояснення в рамках газової динаміки.
При наступному аналізі перебігу газу в соплі Лаваля приймаються наступні допущення:
- Газ вважається ідеальним.
- Газовий потік є ізоентропним (тобто має постійну ентропію, сили тертя і дисипативні втрати не враховуються) і адіабатичним (тобто теплота не підводиться і не відводиться).
- Газовий протік є стаціонарним і одновимірним, тобто в будь фіксованій точці сопла всі параметри потоку постійні в часі і змінюються тільки уздовж осі сопла, причому у всіх точках обраного поперечного перерізу параметри потоку однакові, а вектор швидкості газу всюди паралельний осі симетрії сопла.
- Масова витрата газу однакова у всіх поперечних перерізах потоку.
- Вплив всіх зовнішніх сил і полів (в тому числі гравітаційного) дуже мале.
- Вісь симетрії сопла є просторовою координатою [math]\, x[/math].
Відношення локальної швидкості [math]\,v[/math] до локальної швидкості звуку [math]\, C[/math] позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати [math]\, x[/math]:
З рівняння стану ідеального газу:[math]\frac{dp}{d\rho}=C^2[/math], тут [math]\,\rho[/math] - локальна щільність газу, [math]\, p[/math] - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера приймає вигляд:
якщо врхувати рівняння (1), то отримаємо:
Рівняння (2) є ключовим
Переглянемо його в наступній формі:
Велмчмнм [math]\frac{1}{\rho} \frac{d\rho}{dx}[/math] і [math]\frac{1}{v} \frac{dv}{dx}[/math] характеризують відносну ступінь змінності по координаті [math]\, x[/math] щільності газу і його швидкості відповідно. Причому рівняння (2.1) показує, що співвідношення між цими величинами дорівнює квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність зменшується). Таким чином, на дозвукових швидкостях [math]\, (M \lt 1)[/math] щільність змінюється у меншій мірі, ніж швидкість, а на надзвукових [math]\, (M\gt 1)[/math] - навпаки. Як буде видно далі, це і визначає звужуючо-розширюючу форму сопла.
Оскільки масовий розхід газу постіний:
где [math]\, A[/math] — площа поперечного перерізу сопла,
диференціюючи обидві частини цього рівняння по [math]\, x[/math], отримуємо:
Післяпідстановки з (2) в це рівняння, остаточно отримуємо:
При збільшенні швидкості газу в соплі знак фиразу [math]\frac{A}{v}\cdot\frac{dv}{dx}[/math] додатній і, знак похідниї [math]\frac{dA}{dx}[/math] визначається знаком виразу: [math]\,({M^2 - 1})[/math]
З чого можна зробити наступні висновки:
- При дозвуковій швидкості рух газу [math]\,(M\lt 1)[/math], похідна [math]\frac{dA}{dx}\lt 0[/math] — сопло звужується.
- При надзвуковій швидкості рух газу [math]\,(M\gt 1)[/math], похідна [math]\frac{dA}{dx}\gt 0[/math] — сопло розширюється.
- При русі газу зі швидкістю звуку [math]\,(M = 1)[/math], похідна [math]\frac{dA}{dx}=0[/math] — площа поперечного перерізу досягає екстремума, тобто має місце найвужчий переріз сопла, яке називається критичним.
Отже, на звужуючій, докритичній ділянці сопла рух газу відбувається з дозвуковими швидкостями. У найвужчому, критичному перетині сопла локальна швидкість газу досягає звуковій. На розширюючих, закритичних ділянках, газовий потік рухається з надзвуковими швидкостями. Переміщаючись по соплу, газ розширюється, його температура і тиск падають, а швидкість зростає. Внутрішня енергія газу перетворюється в кінетичну енергію його спрямованого руху. ККД цього перетворення в деяких випадках (наприклад, в соплах сучасних ракетних двигунів) може перевищувати 70%, що значно перевершує ККД реальних теплових двигунів всіх інших типів. Це пояснюється тим, що робоче тіло не передає механічну енергію ніякому посереднику (поршню або лопатям турбіни). В інших теплових двигунах на цій передачі зазнаються значні втрати. Крім того, газ, проходячи через сопло на значній швидкості, не встигає передати його стінкам певну кількість своєї теплової енергії, що дозволяє вважати процес адіабатним. У реальних теплових двигунів інших типів нагрів конструкції становить істотну частину втрат. Автомобільний двигун, наприклад, працює більше на радіатор охолодження, ніж на вихідний вал.
Швидкість виходу газу із сопла
З рівняння стану ідеального газу рівняння стану ідеального газу, і Закон збереження енергії | балансу енергії в газовому потоці виводиться формула розрахунку лінійної швидкості витікання газу з сопла Лаваля:
де:
[math]\,v_e[/math] — Швидкість газу на виході із сопла, м/с,
[math]\,T[/math] — Абсолютна температура газу на вході,
[math]\,R[/math] — Универсальна газова стала [math]\,R=8314,5[/math] Дж/(кіломоль·К),
[math]\,M[/math] — молярна маса газу, кг/кіломоль,
[math]\,k[/math] — Показник адіабати [math]\,k=c_p/c_v[/math],
[math]\,c_p[/math] — Питома теплоємність при при постійному тиску, Дж/(кіломоль·К),
[math]\,c_v[/math] — Удельная теплоёмкость при постоянном объеме, Дж/(кіломоль·К),
[math]\,p_e[/math] — Абсолютний тиск газу на виході із сопла, Па
[math]\,p[/math] — Абсолютний тиск газу на вході в сопло, Па
Перспективи
Прагнення досягти ефективної роботи двигуна як на Землі, так і на висоті змушує конструкторів шукати технічні рішення, що дозволяють досягти цю мету. Одним з таких рішень з'явився рухливий сопловий насадок - «продовження» сопла, яке пристиковується до нього по досягненні ракетою розріджених шарів атмосфери, збільшуючи, таким чином, ступінь розширення сопла. Схема дії насадки зображена на малюнку справа. Ця схема була практично реалізована, зокрема, в конструкції двигуна НК-33-1.
Регульовані сопла винищувача F-15 Проблема оптимізації ступеня розширення сопла дуже актуальна і при розробці авіаційних реактивних двигунів, оскільки літак призначений для польотів в широкому діапазоні висот, а від питомої імпульсу його двигунів в сильній мірі залежить економічність і, отже, дальність польоту. У сучасних турбореактивних двигунах застосовуються регульовані сопла Лаваля. Такі сопла складаються з поздовжніх пластин, що мають можливість переміщення одна відносно одної, зі спеціальним механізмом з гідравлічним або пневматичним приводом, що дозволяє в польоті змінювати площу вихідного і / або критичного перетинів, і, таким чином, домагатися оптимального ступеня розширення сопла при польоті на будь-якій висоті. Регулювання площі прохідних перерізів виконується, як правило, автоматично спеціальною системою управління. Цей же механізм дозволяє по команді пілота змінювати в деяких межах і напрямок реактивного струменя, а отже, напрямок вектора тяги, що істотно підвищує маневреність літака.
Список використаної літератури
- Ландау Л. Д., Ліфшиц Е. М. Розділ X. Одновимірний рух газу. § 97. Витік газу із сопла // Теоретична фізика. — Т. 6. Гідродинаміка.
- Моравський А. В., Файн М. А. Як винаходять теплові двигуни. — М.: Знання, 1990. — 192 с. — (Життя чудових ідей). — 50 000 екз.