Відмінності між версіями «Алгоритм Лемпеля-Зіва»
Tsezar (обговорення • внесок) |
Tsezar (обговорення • внесок) |
||
| Рядок 31: | Рядок 31: | ||
Якщо черговий символ в парі з наступним за ним вже зустрічався то в принципі від цієї пари можна вивести два біта 01 і вказівку на існуючу аналогічну пару. Тоді декодувальник, побачивши 01, по цій вказівці подивиться на вже розшифровану частину тексту, візьме потрібну пару і припише таку саму в кінець розшифрованої частини.<br> | Якщо черговий символ в парі з наступним за ним вже зустрічався то в принципі від цієї пари можна вивести два біта 01 і вказівку на існуючу аналогічну пару. Тоді декодувальник, побачивши 01, по цій вказівці подивиться на вже розшифровану частину тексту, візьме потрібну пару і припише таку саму в кінець розшифрованої частини.<br> | ||
В нашому прикладі достатньо двох байт них посилань. Отже на вихід пошлемо:<br> | В нашому прикладі достатньо двох байт них посилань. Отже на вихід пошлемо:<br> | ||
| − | 001 11 | + | <center>001 11</center> |
Далі від букви Я по відомих правилах піде 9 бітів. Залишок тексту шифрується сімома бітами:<br> | Далі від букви Я по відомих правилах піде 9 бітів. Залишок тексту шифрується сімома бітами:<br> | ||
| − | 00001 01< | + | <center>00001 01</center> |
Перша група з нулів, що закінчується одиницею, означає, що раніше в тексті вже була аналогічна п'ятірка символів. Друга група представляє число одиницю, вказуюче, на якій відстані треба шукати прототип. Прототип добудовуватиметься по ходу будівництва копії з нього, але випереджаючими темпами, достатніми для того, щоб копіювання не простоювало.<br> | Перша група з нулів, що закінчується одиницею, означає, що раніше в тексті вже була аналогічна п'ятірка символів. Друга група представляє число одиницю, вказуюче, на якій відстані треба шукати прототип. Прототип добудовуватиметься по ходу будівництва копії з нього, але випереджаючими темпами, достатніми для того, щоб копіювання не простоювало.<br> | ||
Таким чином, початковий текст в стислому вигляді при декілька вільному зображенні з'явиться у вигляді:<br> | Таким чином, початковий текст в стислому вигляді при декілька вільному зображенні з'явиться у вигляді:<br> | ||
| − | 1 А 1 Би 1 В 001 11 00001 01< | + | <center>1 А 1 Би 1 В 001 11 00001 01</center> |
Правильніше (але менш наочно) було б вписати замість А, Би і В їх восьмибітові уявлення<br>. | Правильніше (але менш наочно) було б вписати замість А, Би і В їх восьмибітові уявлення<br>. | ||
| + | Дерево Лемпеля-Зіва виглядає так:<br> | ||
| + | [[Файл:Derevo.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | Щоб програма розшифровки годилася не тільки для розглянутого прикладу, ще до стислого тексту треба прикласти деякі параметри: довжину стислого або розгорненого тексту, а також довжину посилань. Само дерево прикладати не треба, якщо воно підкоряється простим широкоспоживаним правилам.Отже дерево Лемпеля-Зіва може бути достатнє складним і розлогим.<br> | ||
| + | |||
| + | |||
| + | |||
Версія за 11:25, 28 квітня 2010
| {{{img}}} | ||
| Імя | Володимир | |
| Прізвище | Стодола | |
| По-батькові | Романович | |
| Факультет | ФІС | |
| Група | СН-41 | |
| Залікова книжка | № ПК 06-065 | |
Алгоритм Лемпеля — Зіва(Lempel-ziv, LZ) — це універсальний алгоритм стискування даних без втрат, створений Абрамом Лемпелем (Abraham Lempel), Якобом Зівом (Jacob Ziv) . Він був опублікований Велчем в 1984 році, як покращувана реалізація алгоритму Lz78, опублікованого Лемпелем і Зівом в 1978 році. Алгоритм розроблений так, щоб його можна було швидко реалізувати, але він не обов'язково оптимальний, оскільки він не проводить жодного аналізу вхідних даних.
Історія винекнення
Більше тридцяти років алгоритм стиснення Хаффмана і його варіанти залишалися найбільш популярними методами. Проте в 1977 два дослідники з Ізраїлю запропонували абсолютно інший підхід до цієї проблеми. Абрам Лемпел і Якоб Зів висунули ідею формування "словника" загальних послідовностей даних.
При цьому стиснення даних здійснюється за рахунок заміни записів відповідними кодами із словника. Існують два алгоритми, LZ77 і LZ78. Вони вже не вимагають включення словника даних в архів, оскільки якщо ви формуєте ваш словник визначеним способом, програма декодування може його відновлювати безпосередньо з ваших даних. На жаль, LZ77 і LZ78 витрачають багато часу на створення ефективного словника. Лемпел був запрошений фірмою Sperry для допомоги в розробці способу найбільш ефективної упаковки даних на комп'ютерних стрічках. У цій же фірмі Тері Велч (Terry Welch) розширив алгоритм LZ78, створивши новий варіант, широко відомий, як LZW.
На роботу Велча звернула увагу група програмістів Unix, які використали його алгоритм в їх додатку LZW, що отримав назву compress. Вони додали декілька удосконалень і опублікували загальнодоступну версію цієї програми в телеконференції Internet, завдяки чому багато користувачів змогли почати з нею працювати.
Популярність алгоритму LZW в значній мірі пов'язана з успіхом програми compress. Початковий текст останньої версії програми що здійснює як стиснення, так і декомпресію, займає всього 1200 рядків. Ядро коду стиснення займає не більше сотні рядків, а коду декомпресії не набагато більше. Програмісти вважають, що це полегшує читання і розуміння
алгоритму, а також дозволяє адаптувати його для самих різних цілей.
Метод стиснення
Існує багато практичних алгоритмів стиснення даних, але всі вони базуються на трьох теоретичних способах зменшення надлишковості даних. Перший спосіб полягає в зміні вмісту даних, другий - у зміні структури даних, а третій - в одночасній зміні як структури, так і вмісту даних.
Якщо при стисненні даних відбувається зміна їх вмісту, то метод стиснення є незворотнім, тобто при відновленні (розархівуванні) даних з архіву не відбувається повне відновлення інформації. Такі методи часто називаються методами стиснення з регульованими втратами інформації. Зрозуміло, що ці методи можна застосовувати тільки для таких типів даних, для яких втрата частини вмісту не приводить до суттєвого спотворення інформації. До таких типів даних відносяться відео- та аудіодані, а також графічні дані. Методи стиснення з регульованими втратами інформації забезпечують значно більший ступінь стиснення, але їх не можна застосовувати до текстових даних. Прикладами форматів стиснення з втратами інформації можуть бути: JPEG (Joint Photographic Experts Group) для графічних даних:
- MPG - для для відеоданих;
- MP3 - для аудіоданих
Якщо при стисненні даних відбувається тільки зміна структури даних, то метод стиснення є зворотнім. У цьому випадкові з архіву можна відновити інформацію повністю. Зворотні методи стиснення можна застосовувати до будь-яких типів даних, але вони дають менший ступінь стиснення у порівнянні з незворотними методами стиснення. Приклади форматів стиснення без втрати інформації: GIF (Graphics Interchange Format), TIFF (Tagged Image File Format) - для графічних даних; AVI - для відеоданих; ZIP, ARJ, RAR, CAB, LH - для довільних типів даних. Існує багато різних практичних методів стиснення без втрати інформації, які, як правило, мають різну ефективність для різних типів даних та різних обсягів.
Кодування методом Лемпеля-Зіва
Візьмемо набір символів
АБВАБВЯЯЯЯЯЯ
У нім двічі зустрічається поєднання АБВ, тому його можна записати в так званому словнику, а в початковому тексті тільки залишити силку на словник. Тоді початковий текст можна перетворити, наприклад, в
11ЯЯЯЯЯЯ
і окремо запам'ятати, що за символом 1 насправді ховається трійця АБВ . Ясно, що якщо в тексті поєднання АБВ зустрілося не 2 а 100 або ще краще 1000 разів, то стиснення було б вельми відчутним. Проте в реальних ситуаціях на таке везіння розраховувати не слід. Треба все вичавлювати навіть з небагатьох повторень в початковому тексті. Подивимося, чи багато ми вигадали в розглянутому прикладі.
Текст стискувався на 4 символи, але і, як мінімум, 4 символи опинилися у словнику. Крім того, побудова словника зажадає введення роздільників і ін.
Але і це ще не все. А якщо в тексті вже є символи 1 ? Як зрозуміти, що це саме 1, а не посилання на словник? Як же поступити найбільш грамотно? Ось тут відповідь далеко неоднозначна. Вона і не може бути однозначна, тому що стиснення - це не таблиця множення. Один текст краще стискається одним методом інший - абсолютно іншим способом. Спершу ми розглянемо дуже спрощений варіант, щоб від чого відштовхуватиметься надалі.
Для визначеності вважатимемо, що кожен символ в тексті - це впорядкований набір з 8 бітів, тобто байт, або, що те ж саме ціле число від 0 до 255.
Послідовно читаємо початковий текст і одночасно формуємо вихідний файл. Якщо чергова буква зустрілася вперше, або вона виявилася останньою в тексті, то на вихід посилаємо біт 1 і 8 бітів від самої цієї букви. Так само треба поступити, якщо символ не новий але в парі з наступним ще не зустрічався. Отже в нашому прикладі перші три символи дадуть на виході 27 бітів. Тоді при зворотній операції як тільки той, що розшифровує побачив черговий біт 1, він відразу знатиме, наступні за ним 8 бітів треба вивести, так би мовити відкритим текстом.
Якщо черговий символ в парі з наступним за ним вже зустрічався то в принципі від цієї пари можна вивести два біта 01 і вказівку на існуючу аналогічну пару. Тоді декодувальник, побачивши 01, по цій вказівці подивиться на вже розшифровану частину тексту, візьме потрібну пару і припише таку саму в кінець розшифрованої частини.
В нашому прикладі достатньо двох байт них посилань. Отже на вихід пошлемо:
Далі від букви Я по відомих правилах піде 9 бітів. Залишок тексту шифрується сімома бітами:
Перша група з нулів, що закінчується одиницею, означає, що раніше в тексті вже була аналогічна п'ятірка символів. Друга група представляє число одиницю, вказуюче, на якій відстані треба шукати прототип. Прототип добудовуватиметься по ходу будівництва копії з нього, але випереджаючими темпами, достатніми для того, щоб копіювання не простоювало.
Таким чином, початковий текст в стислому вигляді при декілька вільному зображенні з'явиться у вигляді:
Правильніше (але менш наочно) було б вписати замість А, Би і В їх восьмибітові уявлення
.
Дерево Лемпеля-Зіва виглядає так:
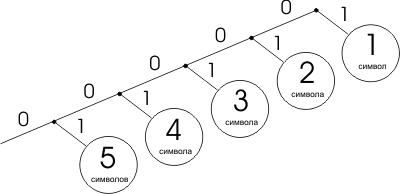
Щоб програма розшифровки годилася не тільки для розглянутого прикладу, ще до стислого тексту треба прикласти деякі параметри: довжину стислого або розгорненого тексту, а також довжину посилань. Само дерево прикладати не треба, якщо воно підкоряється простим широкоспоживаним правилам.Отже дерево Лемпеля-Зіва може бути достатнє складним і розлогим.