Відмінності між версіями «Неньютонівські рідини і їх класифікація»
| (Не показано 13 проміжних версій цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | '''Неньютонівська рідина'''– модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя, спричиненого відносним проковзуванням (зсувом) шарів рідини описуються нелінійною залежністю від градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування. На відміну від ньютонівських рідин, коли динамічний коефіцієнт в'язкості є константою при заданій температурі і тиску, особливість неньютонівських рідин полягає у залежності параметра в'язкості від градієнту швидкості. | + | '''Неньютонівська рідина''' – модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя, спричиненого відносним проковзуванням (зсувом) шарів рідини описуються нелінійною залежністю від градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування. На відміну від ньютонівських рідин, коли динамічний коефіцієнт в'язкості є константою при заданій температурі і тиску, особливість неньютонівських рідин полягає у залежності параметра в'язкості від градієнту швидкості. |
| − | Як синонім до терміну | + | Як синонім до терміну «неньютонівська рідина» вживається, також, термін «аномальна рідина». |
| − | |||
| − | + | ==Закон в'язкого тертя Ньютона == | |
| − | де | + | |
| + | |||
| + | Для ньютонівських рідин закон в’язкого тертя Ньютона матиме вигляд | ||
| + | |||
| + | <math>\tau\ = \mu\(\frac{du}{dn})</math>, | ||
| + | |||
| + | де <math>\tau\</math>— напруження зсуву, що виникають між двома паралельними шарами, що лежать у напрямку потоку; | ||
| + | |||
| + | <math>du/dn</math> — градієнт швидкості, тобто зміна швидкості на одиницю довжини у перпендикулярному до потоку напрямку (швидкісить зсуву); | ||
| + | |||
| + | μ — коефіцієнт пропорційності, який є фізичним параметром і називається динамічною в'язкістю | ||
| + | (як показують дослідження μ залежить від природи рідини або газу, а також від температури). | ||
| + | |||
| + | Для неньютонівських рідин вищенаведений закон не підходить, тобто крива течії не є лінійною. Тому в більш загальному вигляді рівняння слід записати так: | ||
| + | |||
| + | <math>f(\tau\) = \frac{du}{dn}</math> | ||
| + | |||
| + | Очевидно, що для ньютонівських рідин <math>f(\tau\) = \frac{ \tau\ }{ \mu\ } </math>, а для неньютонівських — функція <math>f(\tau\)</math> може мати різний вигляд залежно від роду рідини. | ||
| + | |||
| + | |||
| + | [[Файл:Рисунок1.gif|400px|right| Класифікація рідин за видом залежності дотичних напружень від градієгту швидкості.]] | ||
| + | |||
| + | |||
| + | == Класифікація неньютонівських рідин == | ||
| + | |||
| + | Якщо <math>f(\tau\)= \frac{\tau\ - (\tau_0\)}{\eta\ }</math>, де <math>\tau_0\</math>— граничне напруження зсуву, а <math>\eta\</math>—пластична в’язкість, то рідина являє собою '''''бінгамовський пластик'''''. | ||
| + | |||
| + | Коли ж <math>f(\tau\)= \tau^ (\frac{ \1\ }{ \ n \ } )\ / k </math> , де ''n'' і ''k'' — сталі для даної рідини, то при n<1 маємо так звану '''''псевдопластичну рідину''''', а при n>1 — '''''дилатантну рідину'''''. | ||
| + | |||
| + | Стала ''n'' характеризує ступінь неньютонівської поведінки матеріалу, а k — міру консистенції рідини. | ||
| + | |||
| + | |||
| + | == Бінгамовська рідина == | ||
| + | |||
| + | В статичних умовах бінгамовська рідина веде себе як твердий матеріал, а при силовому впливі починає текти. | ||
| + | |||
| + | Прикладами бінгамовської рідини можуть бути: | ||
| + | <li> шлами | ||
| + | <li> бурові розчини | ||
| + | <li> масляні фарби | ||
| + | <li> стічні води | ||
| + | <li> різні емульсії та інші рідини | ||
| + | |||
| + | |||
| + | == Псевдопластичні рідини == | ||
| + | |||
| + | Псевдопластичні рідини не виявляють меж текучості, і крива течії в них показує, що відношення напруження зсуву і градієнта швидкості, яке в даному випадку характеризує'' уявну'', або ''ефективну'', ''в’язкість'', поступово знижується зі зростанням градієнта швидкості. | ||
| + | |||
| + | Приклади псевдопластичних рідин: | ||
| + | <li> розчини каучука | ||
| + | <li> розчини мастила | ||
| + | <li> розчини полімерів | ||
| + | <li> фармацевтичні розчини | ||
| + | <li> різні харчові продукти | ||
| + | <li> біологічні рідини тощо. | ||
| + | |||
| + | |||
| + | |||
| + | == Дилатантні рідини == | ||
| + | Стаціонарно реологічно аномальна рідина, в'язкість якої із зростанням градієнту швидкості зростає. | ||
| + | |||
| + | Приклади дилатантних рідин: | ||
| + | <li> висококонцентровані водні суспензії порошків двоокису титану, заліза, слюди | ||
| + | <li> системи пісок/вода | ||
| + | <li> гідрозоль крохмалю | ||
| + | <li> солодкі суміші | ||
| + | <li> водні розчини гуміарабіку та ін. | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | Крім перелічених вище існують й інші типи неньютонівськнх рідин (в’язко- і пружнопластичні, еластичні тощо). Для багатьох з них зв’язок між напруженням і градієнтом швидкості залежить також від часу дії напруження і передісторії рідини. Значення їх ефективної в’язкості залежить не лише від швидкості зсуву, але й його тривалості. | ||
| + | |||
| + | |||
| + | |||
| + | == Література == | ||
| + | <li> Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с. | ||
| + | <li> Константінов Ю.М., Гіжа О.О. Технічна механіка рідини і газу: Підручник.- К.: Вища школа, 2002.-277с | ||
| + | <li> Астарита Дж., Марруччи Дж., Основы гидромеханики неньютоновских жидкостей, пер. с англ., М., 1978 | ||
Поточна версія на 13:21, 20 травня 2012
Неньютонівська рідина – модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя, спричиненого відносним проковзуванням (зсувом) шарів рідини описуються нелінійною залежністю від градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування. На відміну від ньютонівських рідин, коли динамічний коефіцієнт в'язкості є константою при заданій температурі і тиску, особливість неньютонівських рідин полягає у залежності параметра в'язкості від градієнту швидкості.
Як синонім до терміну «неньютонівська рідина» вживається, також, термін «аномальна рідина».
Зміст
Закон в'язкого тертя Ньютона
Для ньютонівських рідин закон в’язкого тертя Ньютона матиме вигляд
[math]\tau\ = \mu\(\frac{du}{dn})[/math],
де [math]\tau\[/math]— напруження зсуву, що виникають між двома паралельними шарами, що лежать у напрямку потоку;
[math]du/dn[/math] — градієнт швидкості, тобто зміна швидкості на одиницю довжини у перпендикулярному до потоку напрямку (швидкісить зсуву);
μ — коефіцієнт пропорційності, який є фізичним параметром і називається динамічною в'язкістю (як показують дослідження μ залежить від природи рідини або газу, а також від температури).
Для неньютонівських рідин вищенаведений закон не підходить, тобто крива течії не є лінійною. Тому в більш загальному вигляді рівняння слід записати так:
[math]f(\tau\) = \frac{du}{dn}[/math]
Очевидно, що для ньютонівських рідин [math]f(\tau\) = \frac{ \tau\ }{ \mu\ }[/math], а для неньютонівських — функція [math]f(\tau\)[/math] може мати різний вигляд залежно від роду рідини.
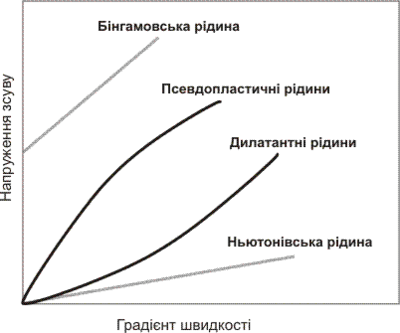
Класифікація неньютонівських рідин
Якщо [math]f(\tau\)= \frac{\tau\ - (\tau_0\)}{\eta\ }[/math], де [math]\tau_0\[/math]— граничне напруження зсуву, а [math]\eta\[/math]—пластична в’язкість, то рідина являє собою бінгамовський пластик.
Коли ж [math]f(\tau\)= \tau^ (\frac{ \1\ }{ \ n \ } )\ / k[/math] , де n і k — сталі для даної рідини, то при n<1 маємо так звану псевдопластичну рідину, а при n>1 — дилатантну рідину.
Стала n характеризує ступінь неньютонівської поведінки матеріалу, а k — міру консистенції рідини.
Бінгамовська рідина
В статичних умовах бінгамовська рідина веде себе як твердий матеріал, а при силовому впливі починає текти.
Прикладами бінгамовської рідини можуть бути:
Псевдопластичні рідини
Псевдопластичні рідини не виявляють меж текучості, і крива течії в них показує, що відношення напруження зсуву і градієнта швидкості, яке в даному випадку характеризує уявну, або ефективну, в’язкість, поступово знижується зі зростанням градієнта швидкості.
Приклади псевдопластичних рідин:
Дилатантні рідини
Стаціонарно реологічно аномальна рідина, в'язкість якої із зростанням градієнту швидкості зростає.
Приклади дилатантних рідин:
Крім перелічених вище існують й інші типи неньютонівськнх рідин (в’язко- і пружнопластичні, еластичні тощо). Для багатьох з них зв’язок між напруженням і градієнтом швидкості залежить також від часу дії напруження і передісторії рідини. Значення їх ефективної в’язкості залежить не лише від швидкості зсуву, але й його тривалості.