Відмінності між версіями «Неньютонівські рідини і їх класифікація»
| Рядок 30: | Рядок 30: | ||
Наприклад, якщо <math>f(\tau\)= \frac{\tau\ - (\tau_0\)}{\eta\ }</math>, де <math>\tau_0\</math>— граничне напруження зсуву, а <math>\eta\</math>—пластична в’язкість, то рідина являє собою '''''бінгамовський пластик'''''. | Наприклад, якщо <math>f(\tau\)= \frac{\tau\ - (\tau_0\)}{\eta\ }</math>, де <math>\tau_0\</math>— граничне напруження зсуву, а <math>\eta\</math>—пластична в’язкість, то рідина являє собою '''''бінгамовський пластик'''''. | ||
| − | Коли ж <math>f(\tau\)= \tau^ (\frac{ \1\ }{ \ | + | Коли ж <math>f(\tau\)= \tau^ (\frac{ \1\ }{ \ n \ } )\ / k </math> , де ''n'' і ''k'' — сталі для даної рідини,то при n<1 маємо так звону '''''псевдопластичну рідину''''', а при n>1 — '''''дилатантну рідину'''''. |
| − | Стала n характеризує ступінь неньютонівської поведінки матеріалу,а k — міру консистенції рідини. | + | Стала ''n'' характеризує ступінь неньютонівської поведінки матеріалу,а k — міру консистенції рідини. |
Версія за 11:11, 20 травня 2012
Неньютонівська рідина– модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя, спричиненого відносним проковзуванням (зсувом) шарів рідини описуються нелінійною залежністю від градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування. На відміну від ньютонівських рідин, коли динамічний коефіцієнт в'язкості є константою при заданій температурі і тиску, особливість неньютонівських рідин полягає у залежності параметра в'язкості від градієнту швидкості.
Як синонім до терміну «неньютонівська рідина» вживається, також, термін «аномальна рідина».
Зміст
Закон в'язкого тертя Ньютона
Для неньютонівських рідин закон в’язкого тертя Ньютона ([math]\tau\ = \mu\(\frac{du}{dn})[/math]) не підходить, тобто крива течії не є лінійною. Тому в більш загальному вигляді рівняння слід записати так:
[math]f(\tau\) = \frac{du}{dn}[/math]
де [math]\tau\[/math]— напруження зсуву, що виникають між двома паралельними шарами,що лежать у напрямку потоку
[math]du/dn[/math] — градієнт швидкості, тобто зміна швидкості на одиницю довжини у перпендикулярному до потоку напрямку (швидкісить зсуву)
μ — коефіцієнт пропорційності, який є фізичним параметром і називається динамічною в'язкістю (як показують дослідження μ залежить від природи рідини або газу, а також від температури)
Очевидно, що для ньютонівських рідин [math]f(\tau\) = \frac{ \tau\ }{ \mu\ }[/math], а для неньютонівських — функція [math]f(\tau\)[/math] може мати різний вигляд залежно від роду рідини.
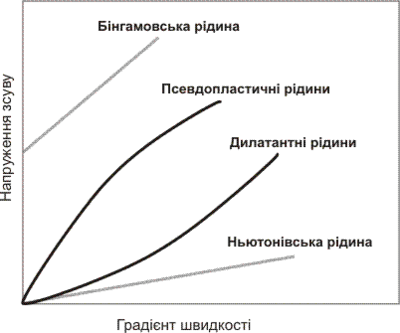
Класифікація неньютонівських рідин
Наприклад, якщо [math]f(\tau\)= \frac{\tau\ - (\tau_0\)}{\eta\ }[/math], де [math]\tau_0\[/math]— граничне напруження зсуву, а [math]\eta\[/math]—пластична в’язкість, то рідина являє собою бінгамовський пластик.
Коли ж [math]f(\tau\)= \tau^ (\frac{ \1\ }{ \ n \ } )\ / k[/math] , де n і k — сталі для даної рідини,то при n<1 маємо так звону псевдопластичну рідину, а при n>1 — дилатантну рідину.
Стала n характеризує ступінь неньютонівської поведінки матеріалу,а k — міру консистенції рідини.
Бінгамовська рідина
Модель Бінгама схожа до моделі сухого тертя. В статичних умовах рідина веде себе як твердий матеріал, а при силовому впливі починає текти
прикладом бінгамовської рідини може бути:
Псевдопластичні рідини
Псевдопластичні рідини не виявляють меж текучості, і крива течії в них показує, що відношення напруження зсуву і градієнта швидкості, яке в даному випадку характеризує уявну, або ефективну, в’язкість, поступово знижується зі зростанням градієнта швидкості. Для дилатантних рідин ефективна в’язкість зростає зі збільшенням швидкості зсуву.
приклади псевдопластичних рідин:
Дилатантні рідини
Стаціонарно реологічно аномальна рідина, в'язкість якої із зростанням градієнту швидкості зростає
прикладом дилатантних рідин є:
Крім перелічених вище існують й інші типи неньютонівськнх рідин (в’язко- і пружнопластичні, еластичні тощо). Для багатьох з них зв’язок між напруженням і градієнтом швидкості залежить також від часу дії напруження і передісторії рідини. Значення їх ефективної в’язкості залежить не лише від швидкості зсуву, але й його тривалості.