Відмінності між версіями «Середня швидкість потоку»
| (Не показані 37 проміжних версій 2 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
=='''Середня швидкість потоку'''== | =='''Середня швидкість потоку'''== | ||
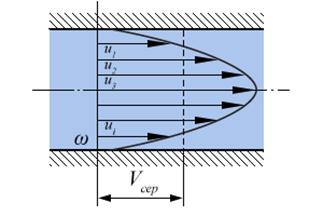
| + | '''Середньою швидкістю потоку''' <math> V </math> м/с у перерізі називається така однакова для всіх точок перерізу потоку швидкість руху речовини, при якій через цей переріз проходить та ж витрата, що і при дійсному розподілі швидкостях руху речовини. | ||
| + | |||
| + | [[Файл:image026.jpg]] | ||
| + | |||
| + | Рис.1. Епюра швидкостей. | ||
Широке коло питань технічної механіки рідини може бути вирішене за допомогою специфічного підходу до вивчення руху рідини, котрий називається методом [http://www.ru.wikipedia.org/wiki/Гидравлика.com ''гідравліки'']. | Широке коло питань технічної механіки рідини може бути вирішене за допомогою специфічного підходу до вивчення руху рідини, котрий називається методом [http://www.ru.wikipedia.org/wiki/Гидравлика.com ''гідравліки'']. | ||
| Рядок 8: | Рядок 13: | ||
[[Файл:Karp.PNG]] | [[Файл:Karp.PNG]] | ||
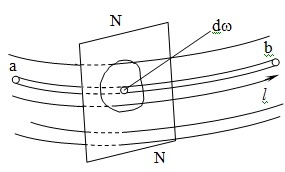
| − | Рис. | + | Рис.2. Рух потоку рідини. |
Потім дійсну течію з різними швидкостями окремих струминок заміняють розрахунковою моделлю потоку, котрий рухається як одне суцільне ціле з сталою для всіх частинок в даному перерізі швидкістю. При такій схематизації течії швидкості і прискорення в напряму, нормальному до основного руху, не враховуються. Для опису такої течії достатньо тільки однієї координати простору – відстані l вздовж вісі потоку від перерізу, що розглядається, відносно деякої початкової точки О. | Потім дійсну течію з різними швидкостями окремих струминок заміняють розрахунковою моделлю потоку, котрий рухається як одне суцільне ціле з сталою для всіх частинок в даному перерізі швидкістю. При такій схематизації течії швидкості і прискорення в напряму, нормальному до основного руху, не враховуються. Для опису такої течії достатньо тільки однієї координати простору – відстані l вздовж вісі потоку від перерізу, що розглядається, відносно деякої початкової точки О. | ||
| Рядок 21: | Рядок 26: | ||
де W – об’єм рідини в м3, який протікає за час t в секундах (хвилинах, годинах) через живий переріз потоку. | де W – об’єм рідини в м3, який протікає за час t в секундах (хвилинах, годинах) через живий переріз потоку. | ||
| − | * | + | * |
''Середня швидкість потоку'' V , м/с, визначається за допомогою формули: | ''Середня швидкість потоку'' V , м/с, визначається за допомогою формули: | ||
| Рядок 30: | Рядок 35: | ||
<math>V = \int_\omega (u) d\omega/\omega</math> | <math>V = \int_\omega (u) d\omega/\omega</math> | ||
| + | |||
| + | == Приклади застосування == | ||
| + | |||
| + | *'''Середня швидкість потоку''' - використовують для обчислення масової витрати. | ||
| + | Масова витрата може бути обчислена через густину речовини, площу перетину потоку і середню швидкість потоку у цьому перетині: | ||
| + | |||
| + | [[Файл:123.PNG]] | ||
| + | |||
| + | де: | ||
| + | |||
| + | Q — масова витрата; | ||
| + | ρ — густина речовини; | ||
| + | V — середня швидкість потоку; | ||
| + | S — площа перетину потоку. | ||
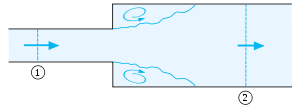
| + | *Також, '''середня швидкість''' потоку використовується у Формулі Борда-Карно. У перетині 1 середня швидкість потоку дорівнює ''V''<sub>1</sub>, тиск становить ''p''<sub>1</sub> і площа поперечного перерізу ''S''<sub>1</sub>. Відповідні величини для потоку у перетині 2 — після розширення становлять ''V''<sub>2</sub>, ''p''<sub>2</sub> і ''S''<sub>2</sub>, відповідно. Коефіцієнт втрат ''ξ'' для цього раптового розширення дорівнює одиниці :''ξ'' = 1,0. Виходячи із закону збереження маси, вважаючи сталою густину рідини ''ρ'', ''об'ємна витрата'' через обидва перерізи повинна бути однаковою (умова нерозривності): | ||
| + | :<math>S_1\, V_1\, = S_2\, V_2</math> звідки <math>V_2\, =\, \frac{S_1}{S_2}\, V_1.</math> | ||
| + | |||
| + | [[Файл:300.svg.png]] | ||
| + | |||
| + | Рис.3. Раптове розширення потоку у трубі. | ||
| + | |||
| + | *'''Використання середньої швидкості''' у формулі Дарсі-Вейсбаха, яка визначає втрати напору або втрати тиску при турбулентному режимі протікання нестискуваної рідини на гідравлічних опорах. | ||
| + | Вперше формула була запропонована Ю. Вейсбахом (J. Weisbach) у 1845 році і була записана у вигляді: | ||
| + | [[Файл:1.PNG]] | ||
| + | |||
| + | де: | ||
| + | Δh — втрати напору на гідравлічному опорі; | ||
| + | ξ — коефіцієнт втрат на тертя; | ||
| + | V — середня швидкість руху рідини; | ||
| + | g — прискорення вільного падіння. | ||
| + | Величина називається швидкісним (або динамічним) напором. | ||
| Рядок 38: | Рядок 74: | ||
[[Файл:Karp1.jpg]] | [[Файл:Karp1.jpg]] | ||
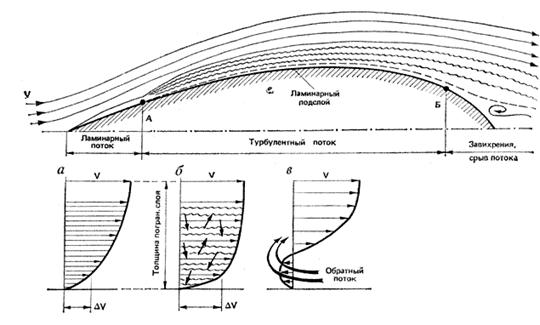
| − | Рис. | + | Рис.4. Режими руху рідини. |
| − | + | Існування двох принципово різних режимів руху рідини було помічено Г.Хагеном у 1839р. При вивченні особливостей протікання рідин з різними фізичними властивостями Рейнольдс встановив, що рух буває : ламінарний (від латинського lamina –шар) і турбулентний (від лат. turbulentus - безладний ). | |
| − | + | Ламінарним називається такий режим, коли потік рідини рухається окремими струминками або шарами і траєкторії окремих часток між собою не перетинаються. На практиці ламінарний режим має місце при русі рідин з великою в'язкістю (нафти, оливи), при русі рідин через тонкі трубки та в трубопроводах при малих швидкостях потоку.(a) | |
| − | + | Турбулентним називається такий режим, коли струминність потоку порушується, всі струминки перемішуються, і траєкторії часток, що рухаються набувають складної форми, перетинаючись між собою. На практиці частіше має місце турбулентний режим руху рідини.(b) | |
| − | Рейнольдс встановив, що критерієм режиму руху рідини є безрозмірна величина, | + | [[Файл:121212.png]] |
| + | |||
| + | В 1883р. Рейнольдс за результатом експериментальних досліджень встановив, що критерієм режиму руху рідини є безрозмірна величина, що являє собою відношення добутку середньої швидкості потоку V і характерного для випадку, що розглядається лінійного розміру L до кінематичної в'язкості рідини ν : VL/ν. Цей критерій (критерій подібності, див. розділ 8.2) називається числом Рейнольдса і позначається Re. Таким чином, число Рейнольдса можна визначити за формулою | ||
| + | |||
| + | [[Файл:image323.gif]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Джерела == | == Джерела == | ||
| Рядок 58: | Рядок 93: | ||
* Колчунов В.І. Теоретична та прикладна гідромеханіка: Навч. Посібник.-К.:НАУ, 2004.-336с. | * Колчунов В.І. Теоретична та прикладна гідромеханіка: Навч. Посібник.-К.:НАУ, 2004.-336с. | ||
* Конспект лекцій з Гідрогазодинаміки для студентів груп КА,КТ. | * Конспект лекцій з Гідрогазодинаміки для студентів груп КА,КТ. | ||
| + | |||
| + | == == | ||
Поточна версія на 14:48, 26 квітня 2012
Середня швидкість потоку
Середньою швидкістю потоку [math]V[/math] м/с у перерізі називається така однакова для всіх точок перерізу потоку швидкість руху речовини, при якій через цей переріз проходить та ж витрата, що і при дійсному розподілі швидкостях руху речовини.
Рис.1. Епюра швидкостей.
Широке коло питань технічної механіки рідини може бути вирішене за допомогою специфічного підходу до вивчення руху рідини, котрий називається методом гідравліки.
Течію рідини подумки розбивають на ряд елементарних струминок,щоб вісь кожної з них була дотична до напрямку швидкості.
Рис.2. Рух потоку рідини.
Потім дійсну течію з різними швидкостями окремих струминок заміняють розрахунковою моделлю потоку, котрий рухається як одне суцільне ціле з сталою для всіх частинок в даному перерізі швидкістю. При такій схематизації течії швидкості і прискорення в напряму, нормальному до основного руху, не враховуються. Для опису такої течії достатньо тільки однієї координати простору – відстані l вздовж вісі потоку від перерізу, що розглядається, відносно деякої початкової точки О.
- Живим перерізом [math]{\omega}[/math] м² називається площа поперечного перерізу потоку, яка нормальна до напрямку течії.
Для розрахунку витрат використовують значення середньої швидкості потоку як усередненої характеристики інтенсивності протікання речовини.
- Витратою потоку [math]Q[/math] м3/c називається об’єм рідини , який протікає за одиницю часу через живий переріз потоку.
[math]Q = \frac{W}{\tau}[/math]
де W – об’єм рідини в м3, який протікає за час t в секундах (хвилинах, годинах) через живий переріз потоку.
Середня швидкість потоку V , м/с, визначається за допомогою формули:
[math]V = \frac{Q} {\omega}[/math]
- Середня швидкість зв’язана з місцевими швидкостями u в окремих точках живого перерізу співвідношеннями:
[math]V = \int_\omega (u) d\omega/\omega[/math]
Приклади застосування
- Середня швидкість потоку - використовують для обчислення масової витрати.
Масова витрата може бути обчислена через густину речовини, площу перетину потоку і середню швидкість потоку у цьому перетині:
де:
Q — масова витрата; ρ — густина речовини; V — середня швидкість потоку; S — площа перетину потоку.
- Також, середня швидкість потоку використовується у Формулі Борда-Карно. У перетині 1 середня швидкість потоку дорівнює V1, тиск становить p1 і площа поперечного перерізу S1. Відповідні величини для потоку у перетині 2 — після розширення становлять V2, p2 і S2, відповідно. Коефіцієнт втрат ξ для цього раптового розширення дорівнює одиниці :ξ = 1,0. Виходячи із закону збереження маси, вважаючи сталою густину рідини ρ, об'ємна витрата через обидва перерізи повинна бути однаковою (умова нерозривності):
- [math]S_1\, V_1\, = S_2\, V_2[/math] звідки [math]V_2\, =\, \frac{S_1}{S_2}\, V_1.[/math]
Рис.3. Раптове розширення потоку у трубі.
- Використання середньої швидкості у формулі Дарсі-Вейсбаха, яка визначає втрати напору або втрати тиску при турбулентному режимі протікання нестискуваної рідини на гідравлічних опорах.
Вперше формула була запропонована Ю. Вейсбахом (J. Weisbach) у 1845 році і була записана у вигляді:
де: Δh — втрати напору на гідравлічному опорі; ξ — коефіцієнт втрат на тертя; V — середня швидкість руху рідини; g — прискорення вільного падіння. Величина називається швидкісним (або динамічним) напором.
Режими руху рідини
Режими руху рідини. Критерій Рейнольдса.
Рис.4. Режими руху рідини.
Існування двох принципово різних режимів руху рідини було помічено Г.Хагеном у 1839р. При вивченні особливостей протікання рідин з різними фізичними властивостями Рейнольдс встановив, що рух буває : ламінарний (від латинського lamina –шар) і турбулентний (від лат. turbulentus - безладний ).
Ламінарним називається такий режим, коли потік рідини рухається окремими струминками або шарами і траєкторії окремих часток між собою не перетинаються. На практиці ламінарний режим має місце при русі рідин з великою в'язкістю (нафти, оливи), при русі рідин через тонкі трубки та в трубопроводах при малих швидкостях потоку.(a)
Турбулентним називається такий режим, коли струминність потоку порушується, всі струминки перемішуються, і траєкторії часток, що рухаються набувають складної форми, перетинаючись між собою. На практиці частіше має місце турбулентний режим руху рідини.(b)
В 1883р. Рейнольдс за результатом експериментальних досліджень встановив, що критерієм режиму руху рідини є безрозмірна величина, що являє собою відношення добутку середньої швидкості потоку V і характерного для випадку, що розглядається лінійного розміру L до кінематичної в'язкості рідини ν : VL/ν. Цей критерій (критерій подібності, див. розділ 8.2) називається числом Рейнольдса і позначається Re. Таким чином, число Рейнольдса можна визначити за формулою
Джерела
- Ландау Лев Давидович | Ландау Л.Д., Ліфшиц, Євген Михайлович | Ліфшиц О.М. - Курс теоретичної фізики Ландау і Ліфшиця | Теоретична фізика (Том 6. Гідродинаміка). Глава III. В'язка рідина. § 17. Середня швидкість потоку. Течії.
- Колчунов В.І. Теоретична та прикладна гідромеханіка: Навч. Посібник.-К.:НАУ, 2004.-336с.
- Конспект лекцій з Гідрогазодинаміки для студентів груп КА,КТ.