Відмінності між версіями «Методи визначення в'язкості»
(→Ротаційний метод) |
(→Ротаційний метод) |
||
| Рядок 129: | Рядок 129: | ||
де <math>\varepsilon=\frac{R_{o}}{R_{i}}</math>; <math>\omega</math> - кутова швидкість обертання ротора. | де <math>\varepsilon=\frac{R_{o}}{R_{i}}</math>; <math>\omega</math> - кутова швидкість обертання ротора. | ||
| − | Якщо зовнішній циліндр відсутній <math>(R_{o}\to\ | + | Якщо зовнішній циліндр відсутній <math>(R_{o}\to\infty)</math>, в'язкість обчислюють за формулою: |
<math>\eta=\frac{M}{4\pi H R_{i}^2\omega}</math> | <math>\eta=\frac{M}{4\pi H R_{i}^2\omega}</math> | ||
Версія за 21:33, 25 квітня 2012
Зміст
Загальні положення
В сучасних умовах розвитку промисловості і транспорту України актуальним є підвищення надійності й ефективності функціювання технологічного обладнання, що безпосередньо пов’язано з необхідністю раціонального підбору і використання палива, олив, мастил та спеціальних рідин.
- В’язкість і густина є основними фізико-хімічними параметрами, що визначають властивості та характеризують склад й структуру нафтопродуктів, більшість з яких є ньютонівськими рідинами.
У зв’язку з цим, кінематична в’язкість і густина займають важливе значення в системі нормованих показників палива для реактивних, газотурбінних і дизельних двигунів та мазуту, а для всіх видів олив й мастил - кінематична в’язкість є обов’язковим показником якості, що визначає їх хіммотологічні властивості.
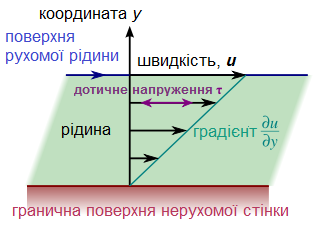
- В'язкість або внутрішнє тертя - властивість текучих тіл рідин і газів чинити опір переміщенню однієї їх частини відносно іншої,
характеристика сил внутрішнього тертя. Сила тертя залежно від в'язкості, рідини або газу виражається формулою:
[math]F= -\mu\frac{\partial v}{\partial l}[/math]
де F - сила опору переміщенню шарів середовища, що спрямоване убік убування швидкості (знак мінус у формулі).
Рідини, характеристики в'язкості яких опусуються вище заданими ріняннями називаються ньютонівськими або ідеально в'язкими.
Рис.1 Розподіл швидкості у ньютонівській рідині
- Одиниця в'язкості в системі СВ - Паскаль секунда. У системі CGS одиниця в'язкості - Пуаз:
1Па с = 10 Пуаз.
Іноді в техніці користуються поняттям питомої в'язкості, тобто відношенням в'язкості рідини до в'язкості води:
[math]A=\frac{\mu}{\mu}[/math]
Існує поняття кінематичної в'язкості - це в'язкість, віднесена до одиничної щільності, тобто:
- [math]\nu=\frac{\mu}{\rho}[/math]
Виміряється кінематична в'язкість в одиницях L2T-1 , тобто M2 /сек у системі СВ. Та ж одиниця в Сгс-Системі називається стоксом 1Стокс.
Віскозиметри
Прилади для виміру в'язкості називаються віскозиметрами. У віскозиметрах використовуються два різних принципи: -по швидкості витікання рідини з малого отвору або з капіляра; -по швидкості падіння кульки в грузлої рідини.
- Перший принцип заснований на формулі Пуазейля, що дає залежність між об'ємом рідини, що випливає із трубки радіусом R і довжиною I:
[math]V=\frac{1}{\mu}\frac{\pi R^4}{8l }+(P1-P2)t[/math]
де P1 і P2 - тиск на торцях трубки; R - радіус трубки; I - довжина; t - час витікання.
- Другий принцип виміру в'язкості заснований на вимірі швидкості падіння кулі в грузлому середовищу (формула Стокса):
[math]V=\frac{2(\rho-\rho')qr^2}{9\mu}[/math]
де v - швидкість падіння кулі в рідині; р - щільність матеріалу кулі; р' - щільність рідини; r - радіус кулі.
Віскозиметри Брукфильда підрозділяються на три основних типи: аналогові (із круговою шкалою), цифрові й програмувальні. Основне розходження між ними полягає в способі відображення результатів. В аналогових віскозиметрів результат зчитується по покажчику на круговій шкалі, а в цифрових виводиться на дисплей. Крім того, цифрові віскозиметри обладнані аналоговим виходом 0-10 мВ, до якого можна підключити різні зовнішні пристрої, такі як дисплей, контролер або самопис. Внутрішній пристрій аналогових і цифрових віскозиметрів практично однаково й також однакова методика використання.
Методи визначення в'язкості
Методи вимірювання в’язкості підрозділяються на дві групи:
- при протіканні середовища через канали:
а) метод капілярного витікання (віскозиметри); б) вібраційні; в) ротаційні методи.
- при русі твердого тіла в середовищі:
а) метод падаючої кульки; б) пенетрація; в) пластометрія.
Метод капілярного витікання
Метод капілярного витікання базується на використанні формули Гагена–Пуазейля, згідно з якою об’єм рідини V, що протікає за час t через капіляр (трубку малого поперечного перетину) довжиною l та радіусом R при наявності перепаду тиску ΔP на кінцях капіляра, дорівнює:
[math]V=\frac{\pi R^4\Delta P t}{8\eta l}[/math]
Закон Пуазейля описує закономірності руху рідини в капілярі. Вимірявши об’єм, різницю тисків та знаючи геометричні розміри труби, можна визначити коефіцієнт в’язкості:
[math]\eta=\frac{\pi R^4\Delta P t}{8 l V}[/math]
Вібраційний метод
Вібраційний метод заснований на визначенні змін параметрів вимушених коливань тіла при зануренні його у в’язке середовище. Метод вимагає створення складної електромеханічної коливальної системи. Вимірюється логарифмічний декремент затухання коливань системи у середовищі k і без нього k'. Тоді
[math]\eta=\frac{k-k'}{\tau C}[/math]
де [math]\tau[/math] - тривалість одного повного коливання; C - деяка константа, що визначається типом вимірювального приладу. Найкраще її визначити для середовища відомої в’язкості.
Метод падаючої кульки
Метод падаючої кульки (метод Стокса) заснований на дослідженні падіння кульки радіусу R в рідині, поміщеній в циліндричну склядну посудину.
Через деякий час після падіння рух кульки стає рівномірним. Це свідчить про те, що сили, які на неї діяли, врівноважились, а саме:
[math]F_{t}=F_{a}+F_{c}[/math]
де [math]F_{t}[/math] - сила тяжіння; [math]F_{a}[/math] - сила виштовхування (Архімедові сила); [math]F_{c}[/math] - сила опору внаслідок в’язкості (сила Стокса).
Сила опору твердому тілу,що падає в рідині, сила Стокса є:
[math]F_{c}=6\pi V R\eta[/math]
де [math]\eta[/math] – в’язкість рідини; R - радіус кульки; V - швидкість кульки.
Підкладаючи у форму рівності сил їх значення, маємо:
[math]\frac{4}{3}\pi R^3\rho_{k} g=\frac{4}{3}\pi R^3\rho_{p}g+6\pi R V\eta[/math]
Звідси одержуємо робочу формулу Стокса:
[math]\eta=\frac{2 R^2 (\rho_{k}-\rho_{p})g}{9 V}[/math]
Ротаційний метод
Ротаційний метод побудований на вимірюванні обертального моменту М, який виникає на осі ротора (циліндра, диска і т.п.), зануреного у вимірювальне середовище, при взаємному їх переміщенні.
В одному з основних варіантів методу шар досліджуваної рідини висотою Н перебуває між двома коаксіальними циліндрами з внутрішніми радіусами [math]R_{i}[/math] і [math]R_{o}[/math] ([math]R_{i}[/math]<[math]R_{o}[/math]), які обертаються один щодо іншого.
В'язкість обчислюється за формулою Маргулеса:
[math]\eta=\frac{M(\varepsilon^2-1)}{4\pi H\varepsilon^2\omega}[/math]
де [math]\varepsilon=\frac{R_{o}}{R_{i}}[/math]; [math]\omega[/math] - кутова швидкість обертання ротора.
Якщо зовнішній циліндр відсутній [math](R_{o}\to\infty)[/math], в'язкість обчислюють за формулою:
[math]\eta=\frac{M}{4\pi H R_{i}^2\omega}[/math]
Див. також
Джерела
- Колчунов В.І. Теоретична та прикладна гідромеханіка: Навч. Посібник.-К.:НАУ, 2004.-336с.
- Конспект лекцій з Гідрогазодинаміки для студентів груп КА,КТ.