Відмінності між версіями «Розкладання дисперсії на складові»
(Створена сторінка: {{Завдання|Пріян Н.|Назаревич О. Б.|14 березня 2012}}) |
|||
| (Не показані 9 проміжних версій 2 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
{{Завдання|Пріян Н.|Назаревич О. Б.|14 березня 2012}} | {{Завдання|Пріян Н.|Назаревич О. Б.|14 березня 2012}} | ||
| + | |||
| + | Розглянемо задачу розкладання дисперсії як характеристики коливальності (розкиду, розсіювання, зміни) на простому абстрактному прикладі. | ||
| + | |||
| + | Нехай вимірювана величина <math>y</math> набувала в <math>N</math> дослідах таких значень <math>y_1,y_2,y_3, ..., y_k, ..., y_N</math>, які характеризуються деякими середніми <math>\overline{y}</math> та оцінкою дисперсії <math>S_y^2</math>. Відкладемо результати вимірювань <math>y</math> на осі ординат (рис. 1), а вісь абсцис для одного із випливаючих на <math>y</math> фаторів <math>x</math>. | ||
| + | |||
| + | [[Файл:Img1.jpg ]] | ||
| + | |||
| + | Рисунок - 1 | ||
| + | |||
| + | |||
| + | Відрізком довжиною <math>S_y</math> зобразимо показник загального розкиду значення <math>y</math> (скористатися дисперсією <math>S_y^2</math> не можна, оскільки її розмірність не збігається з розмірністю <math>y</math>). Припустимо, що одночасно з <math>y</math> реєструвалася величина певного фактора, який за припущенням впливає на <math>y</math>. Цей фактор в усіх дослідах набував лише трьох значень. Результати сумісних вимірювань пар значень <math>y</math> і <math>x</math> зображено на рис. 2. помітна загальна тенденція зростання <math>y</math> зі збільшенням <math>x</math>. Однак говорять лише про зміни <math>y</math> у середньому. оскільки в окремих випадках спостерігається , наприклад <math>y_1>y_5</math>, хоча <math>y_5</math> відповідає більшому <math>x</math>. Ішими словами, кожному <math>x_i</math> відповідає середнє <math>y_i</math>, яке можна розрахувати у даному випадку за чотирма значеннями <math>y</math>. Умовні середні <math>y_i</math> зображено на рис. 3. Розглядаючи <math>\overline{y_i}</math> як самостійні значення, говорять про їх розкид відносно загального середнього <math>\overline{y_i}</math>. Охарактеризуємо цей розкид величиною <math>S^2_{y/x}</math>, яка при певному числі дослідів (в даному випадку 3) залежить від суми квадратів відхилень умовних середніх <math>\overline{y_i}</math> від загального середнього <math>\overline{y}</math>. | ||
| + | |||
| + | [[Файл:Img2.jpg ]] [[Файл:Img3.jpg ]] | ||
| + | |||
| + | Рисунок - 2 Рисунок -3 | ||
| + | |||
| + | |||
| + | Природно, що від того, наскільки зміни <math>x</math> впливають на середні зміни <math>y</math>, залежать значення <math>S^2_{y/x}</math> і показник загального розкиду <math>S^2_y</math>. | ||
| + | Зазначимо, що при одному й тому ж значенні <math>x</math> в чотирьох дослідах дістали різні значення <math>y</math> (див. рис. 2). Наявність даного розкиду при фіксованому значенні фактора <math>x</math> пояснюється діянням невраховуваних факторів <math>z</math>, тобто різними випадковими причинами. Не виділяючи будь-яку з них, охарактеризуємо сумарний ефект від них залишковою дисперсією <math>S^2_{y/z}</math>, яка, представляючи розкид результатів вимірювань <math>y</math> відносно <math>\overline{y}</math>, залежить від суми квадратів відхилень <math>y</math>, виміряних при кожному значенні <math>x</math>, від відповідних умовних середніх <math>\overline{y_i}</math>. На рис. 3 відрізками зображено показник розкиду для кожного <math>x</math>, а також показник розкиду <math>S_{y/x}</math> середніх значень <math>\overline{y_i}</math>. | ||
| + | |||
| + | Очевидно, що, коли усунути вплив невраховуваних факторів, розкид <math>y</math> при фіксованому <math>x</math> не спостерігатиметься і загальний розкид <math>y</math> визначатиметься тільки діяннями <math>x</math> (див. рис. 4). З іншого боку, якби вплив фактора <math>x</math> на <math>y</math> був відсутній, а випадкові причини виявляли своє діяння (див. рис. 5), то загальний розкид <math>y</math> визначався б тільки ними і характеризувався лише залишковою дисперсією від діяння невраховуваних факторів. | ||
| + | |||
| + | [[Файл:Img4.jpg ]] [[Файл:Img5.jpg ]] | ||
| + | |||
| + | Рисунок - 4 Рисунок - 5 | ||
| + | |||
| + | |||
| + | Детально розглянемо основні принципи сучасного експерименту: рандомізацію, багатофакторність, оптимізацію та автоматизацію. Пояснимо перший з них. Дисперсійний аналіз стає об’єктивним інструментом дослідження лише при умові, що кожне значення змінної вибрано з генеральної сукупності випадковим чином. Відбір випадкових значень змінної, який забезпечує однакову імовірність потрапити до вибірки будь-якого з них для всієї генеральної сукупності, називається рандомізацією (від англійського random – вибраний навмання). У біометрії це слово прийнято записувати і вимовляти як рендомізація. Щоб забезпечити однакову імовірність для будь-якого члена генеральної сукупності, найчастіше користуються таблицею випадкових чисел. | ||
| + | |||
| + | Таким чином, при сумісності діяння фактора <math>x</math> та випадкових причин <math>z</math> наступною буде рівність | ||
| + | <math>S^2= S^2_{y/x}+ S^2_{y/z}</math>, | ||
| + | яка і виражає властивість адитивної дисперсії. | ||
| + | |||
| + | Зазначимо, що ця формула правильна лише при незалежних (некорельованих) факторах, які впливають на <math>y</math>. У противному разі вона ускладнюється: | ||
| + | <math>S^2= S^2_{y/x} + S^2_{y/z} - 2 S_{y/x} S_{y/z} r_{xz} </math>, | ||
| + | де <math> r_{xz}</math> - коефіцієнт кореляції. | ||
| + | |||
| + | Формула адитивності дисперсії є основною всього дисперсійного аналізу. Її застосування часто зустрічається з боку експерименту внутрішній опір. Оскільки при всій своїй простоті вона не є очевидною. Тому, перш ніж дістати на основі цієї формули розрахункові рівняння, доведемо її правильність. Для цього скористаємось формальним перетворенням суми квадратів відхилень від загального середнього: | ||
| + | <math>\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y})^2 = \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i} + \overline{y_j} + \overline{y})^2 + \sum_{j=1}^n \sum_{i=1}^m [(y_{ij} - \overline{y_i}) + (\overline{y_i} - \overline{y})]^2 = </math> | ||
| + | |||
| + | <math> = \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})^2 + \sum_{j=1}^n \sum_{i=1}^m (\overline{y_i} - \overline{y})^2 + 2\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})(\overline{y_i}-\overline{y}) </math>. | ||
| + | |||
| + | Враховуючи, що | ||
| + | <math> \overline{y_i} = \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij} </math> ; | ||
| + | |||
| + | <math> \overline{y} = \frac{\mathrm 1}{\mathrm mn}\, \sum_{j=1}^n \sum_{i=1}^m y_ij = \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij} = \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m \overline{y_i} </math>; | ||
| + | |||
| + | <math> \sum_{j=1}^n \overline{y_i} = n \overline{y_i} </math> ; | ||
| + | <math> \sum_{j=1}^n \overline{y} = n \overline{y} </math> , | ||
| + | |||
| + | покажемо, як останній доданок при розкладанні перетворюється в нуль: | ||
| + | |||
| + | <math> \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})(\overline{y_i}-\overline{y}) = \sum_{j=1}^n \sum_{i=1}^m y_{ij}\overline{y_i} - \sum_{j=1}^n \sum_{i=1}^m \overline{y_i} \overline{y_i} - </math> | ||
| + | |||
| + | <math> - \sum_{j=1}^n \sum_{i=1}^m y_{ij} \overline{y} + \sum_{j=1}^n \sum_{i=1}^m \overline{y_i} \overline{y} = \sum_{i=1}^m \overline{y_i} n \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij}-</math> | ||
| + | |||
| + | <math> - \sum_{i=1}^m \overline{y_i} \sum_{j=1}^n \overline{y_i} - mn \frac{\mathrm 1}{\mathrm mn}\, \sum_{j=1}^n \sum_{i=1}^m y_{ij} y + m \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m y_i \sum_{j=1}^n \overline{y} = </math> | ||
| + | |||
| + | <math> = \sum_{i=1}^m n \overline{y_i} \overline{y_i} - \sum_{i=1}^m n \overline{y_i} \overline{y_i} - m n \overline{y} \overline{y} + m n \overline{y} \overline{y}= 0 </math> | ||
| + | |||
| + | Отже, | ||
| + | |||
| + | <math> \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})^2 = \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y})^2 + \sum_{j=1}^n \sum_{i=1}^m (\overline{y_i} - \overline{y})^2 </math>, | ||
| + | |||
| + | що й треба було довести, оскільки | ||
| + | <math> S^2_y \approx \sum \sum (y_{ij} - \overline{y})^2 </math>; <math> S^2_{y/x} \tilde \sum \sum (y_{ij} - \overline{y_i})^2 </math>; <math> S^2_{y/z} \approx \sum \sum (\overline{y_i} - \overline{y})^2 </math>. | ||
| + | |||
| + | Другий доданок в здобутому результаті містить тільки одну змінну <math> y_i </math>, яка підсумовується за <math> m </math> . Тому підсумовування за змінною <math> j</math> сталою <math> (\overline{y_i} - \overline{y})^2 </math> рівнозначне помноженню на <math> n </math>, тобто <math> \sum_{j=1}^n = n </math>, тоді | ||
| + | <math> \sum_{j=1}^n \sum_{i=1}^m = (\overline{y_i} - \overline{y})^2 = \sum_{i=1}^m n (\overline{y_i} - \overline{y})^2 </math>. | ||
| + | |||
| + | Така сума називається зваженою, оскільки <math>n</math> у загальному випадку для кожного <math>i</math> може бути різними. | ||
| + | |||
| + | При використанні дисперсійного аналізу запишемо останні формули через вихідні значення <math>y_{ij}</math>: | ||
| + | <math> \sum \sum (y_{ij} - \overline{y})^2 = \sum \sum y^2_{ij} + \sum \sum \overline{y^2} + 2 \sum \sum y_{ij} \overline{y} = </math> | ||
| + | <math> \sum \sum y_{ij}^2 + m n \overline{y^2} - 2 m n y^2 = \sum \sum y^2_{ij} - m n \overline{y^2} = </math> | ||
| + | <math> \sum \sum y_{ij}^2 - \frac{\mathrm mn}{\mathrm m^2 n^2}\, (\sum \sum y_{ij})^2 = \sum_{j=1}^n \sum_{i=1}^m y^2_{ij} - \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 </math>; | ||
| + | <math> \sum \sum (\overline{y_i} - \overline{y})^2 - \sum^n \sum^m \overline{y^2_i} + \sum^n \sum^m \overline{y^2} - 2\sum^n \sum^m \overline{y_i} \overline{y} = </math> | ||
| + | <math> \sum^n \sum^m y^2_i + \frac{\mathrm mn}{\mathrm m^2 n^2}\, (\sum \sum y_{ij})^2 - 2 m \overline{y} n \overline{y} = </math> | ||
| + | <math> \sum^2 n \frac{\mathrm 1}{\mathrm n^2}\, (\sum^n y_{ij})^2 + \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 - 2 \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 = </math> | ||
| + | <math> = \frac{\mathrm 1}{\mathrm n}\, \sum^m (\sum^n y_{ij})^2 - \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 </math>; | ||
| + | |||
| + | <math> \sum \sum (y_{ij} - \overline{y_i})^2 = \sum \sum y^2_{ij} + \sum \sum \overline{y^2_i} - 2 \sum \sum y_{ij} \overline{y_i} = </math> | ||
| + | <math> \sum^m \sum^n y^2_{ij} + n\sum^m y^2_i - 2\sum^m \sum^n y_{ij} \frac{\mathrm 1}{\mathrm n}\, \sum^n y_{ij} = </math> | ||
| + | <math>\sum \sum y^2_{ij} +n \sum^m \frac{\mathrm 1}{\mathrm n^2}\, (\sum^n y_{ij})^2 - 2\sum^m \frac{\mathrm 1}{\mathrm n}\, (\sum^n y_{ij})^2 = </math> | ||
| + | <math> \sum \sum y^2_{ij} - \frac{\mathrm 1}{\mathrm n}\, \sum^m (\sum^n y_{ij})^2 </math>. | ||
| + | |||
| + | Ці формули є робочими при одно факторному дисперсійному аналізі. Якщо розглядати дисперсії не функції, а не залежного параметра, а замість <math>y</math> покласти <math>x</math>, то структура формул зберігатиметься. | ||
| + | |||
| + | ==Посилання== | ||
| + | В.О. АНІСТРАТЕНКО, В.Г. ФЕДОРОВ. Математичне планування експериментів в АПК: Навч. посібник. - К.: Вища шк., 1993. - 375 с.: іл. | ||
| + | |||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 10:33, 20 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
Розглянемо задачу розкладання дисперсії як характеристики коливальності (розкиду, розсіювання, зміни) на простому абстрактному прикладі.
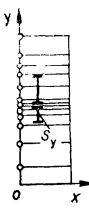
Нехай вимірювана величина [math]y[/math] набувала в [math]N[/math] дослідах таких значень [math]y_1,y_2,y_3, ..., y_k, ..., y_N[/math], які характеризуються деякими середніми [math]\overline{y}[/math] та оцінкою дисперсії [math]S_y^2[/math]. Відкладемо результати вимірювань [math]y[/math] на осі ординат (рис. 1), а вісь абсцис для одного із випливаючих на [math]y[/math] фаторів [math]x[/math].
Рисунок - 1
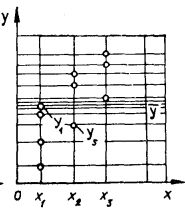
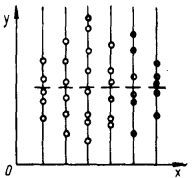
Відрізком довжиною [math]S_y[/math] зобразимо показник загального розкиду значення [math]y[/math] (скористатися дисперсією [math]S_y^2[/math] не можна, оскільки її розмірність не збігається з розмірністю [math]y[/math]). Припустимо, що одночасно з [math]y[/math] реєструвалася величина певного фактора, який за припущенням впливає на [math]y[/math]. Цей фактор в усіх дослідах набував лише трьох значень. Результати сумісних вимірювань пар значень [math]y[/math] і [math]x[/math] зображено на рис. 2. помітна загальна тенденція зростання [math]y[/math] зі збільшенням [math]x[/math]. Однак говорять лише про зміни [math]y[/math] у середньому. оскільки в окремих випадках спостерігається , наприклад [math]y_1\gt y_5[/math], хоча [math]y_5[/math] відповідає більшому [math]x[/math]. Ішими словами, кожному [math]x_i[/math] відповідає середнє [math]y_i[/math], яке можна розрахувати у даному випадку за чотирма значеннями [math]y[/math]. Умовні середні [math]y_i[/math] зображено на рис. 3. Розглядаючи [math]\overline{y_i}[/math] як самостійні значення, говорять про їх розкид відносно загального середнього [math]\overline{y_i}[/math]. Охарактеризуємо цей розкид величиною [math]S^2_{y/x}[/math], яка при певному числі дослідів (в даному випадку 3) залежить від суми квадратів відхилень умовних середніх [math]\overline{y_i}[/math] від загального середнього [math]\overline{y}[/math].
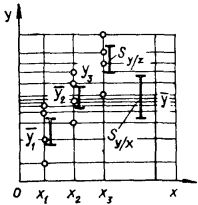
Рисунок - 2 Рисунок -3
Природно, що від того, наскільки зміни [math]x[/math] впливають на середні зміни [math]y[/math], залежать значення [math]S^2_{y/x}[/math] і показник загального розкиду [math]S^2_y[/math].
Зазначимо, що при одному й тому ж значенні [math]x[/math] в чотирьох дослідах дістали різні значення [math]y[/math] (див. рис. 2). Наявність даного розкиду при фіксованому значенні фактора [math]x[/math] пояснюється діянням невраховуваних факторів [math]z[/math], тобто різними випадковими причинами. Не виділяючи будь-яку з них, охарактеризуємо сумарний ефект від них залишковою дисперсією [math]S^2_{y/z}[/math], яка, представляючи розкид результатів вимірювань [math]y[/math] відносно [math]\overline{y}[/math], залежить від суми квадратів відхилень [math]y[/math], виміряних при кожному значенні [math]x[/math], від відповідних умовних середніх [math]\overline{y_i}[/math]. На рис. 3 відрізками зображено показник розкиду для кожного [math]x[/math], а також показник розкиду [math]S_{y/x}[/math] середніх значень [math]\overline{y_i}[/math].
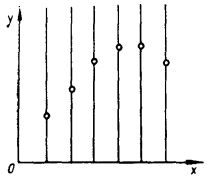
Очевидно, що, коли усунути вплив невраховуваних факторів, розкид [math]y[/math] при фіксованому [math]x[/math] не спостерігатиметься і загальний розкид [math]y[/math] визначатиметься тільки діяннями [math]x[/math] (див. рис. 4). З іншого боку, якби вплив фактора [math]x[/math] на [math]y[/math] був відсутній, а випадкові причини виявляли своє діяння (див. рис. 5), то загальний розкид [math]y[/math] визначався б тільки ними і характеризувався лише залишковою дисперсією від діяння невраховуваних факторів.
Рисунок - 4 Рисунок - 5
Детально розглянемо основні принципи сучасного експерименту: рандомізацію, багатофакторність, оптимізацію та автоматизацію. Пояснимо перший з них. Дисперсійний аналіз стає об’єктивним інструментом дослідження лише при умові, що кожне значення змінної вибрано з генеральної сукупності випадковим чином. Відбір випадкових значень змінної, який забезпечує однакову імовірність потрапити до вибірки будь-якого з них для всієї генеральної сукупності, називається рандомізацією (від англійського random – вибраний навмання). У біометрії це слово прийнято записувати і вимовляти як рендомізація. Щоб забезпечити однакову імовірність для будь-якого члена генеральної сукупності, найчастіше користуються таблицею випадкових чисел.
Таким чином, при сумісності діяння фактора [math]x[/math] та випадкових причин [math]z[/math] наступною буде рівність [math]S^2= S^2_{y/x}+ S^2_{y/z}[/math], яка і виражає властивість адитивної дисперсії.
Зазначимо, що ця формула правильна лише при незалежних (некорельованих) факторах, які впливають на [math]y[/math]. У противному разі вона ускладнюється: [math]S^2= S^2_{y/x} + S^2_{y/z} - 2 S_{y/x} S_{y/z} r_{xz}[/math], де [math]r_{xz}[/math] - коефіцієнт кореляції.
Формула адитивності дисперсії є основною всього дисперсійного аналізу. Її застосування часто зустрічається з боку експерименту внутрішній опір. Оскільки при всій своїй простоті вона не є очевидною. Тому, перш ніж дістати на основі цієї формули розрахункові рівняння, доведемо її правильність. Для цього скористаємось формальним перетворенням суми квадратів відхилень від загального середнього: [math]\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y})^2 = \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i} + \overline{y_j} + \overline{y})^2 + \sum_{j=1}^n \sum_{i=1}^m [(y_{ij} - \overline{y_i}) + (\overline{y_i} - \overline{y})]^2 =[/math]
[math]= \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})^2 + \sum_{j=1}^n \sum_{i=1}^m (\overline{y_i} - \overline{y})^2 + 2\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})(\overline{y_i}-\overline{y})[/math].
Враховуючи, що [math]\overline{y_i} = \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij}[/math] ;
[math]\overline{y} = \frac{\mathrm 1}{\mathrm mn}\, \sum_{j=1}^n \sum_{i=1}^m y_ij = \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij} = \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m \overline{y_i}[/math];
[math]\sum_{j=1}^n \overline{y_i} = n \overline{y_i}[/math] ; [math]\sum_{j=1}^n \overline{y} = n \overline{y}[/math] ,
покажемо, як останній доданок при розкладанні перетворюється в нуль:
[math]\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})(\overline{y_i}-\overline{y}) = \sum_{j=1}^n \sum_{i=1}^m y_{ij}\overline{y_i} - \sum_{j=1}^n \sum_{i=1}^m \overline{y_i} \overline{y_i} -[/math]
[math]- \sum_{j=1}^n \sum_{i=1}^m y_{ij} \overline{y} + \sum_{j=1}^n \sum_{i=1}^m \overline{y_i} \overline{y} = \sum_{i=1}^m \overline{y_i} n \frac{\mathrm 1}{\mathrm n}\, \sum_{j=1}^n y_{ij}-[/math]
[math]- \sum_{i=1}^m \overline{y_i} \sum_{j=1}^n \overline{y_i} - mn \frac{\mathrm 1}{\mathrm mn}\, \sum_{j=1}^n \sum_{i=1}^m y_{ij} y + m \frac{\mathrm 1}{\mathrm m}\, \sum_{i=1}^m y_i \sum_{j=1}^n \overline{y} =[/math]
[math]= \sum_{i=1}^m n \overline{y_i} \overline{y_i} - \sum_{i=1}^m n \overline{y_i} \overline{y_i} - m n \overline{y} \overline{y} + m n \overline{y} \overline{y}= 0[/math]
Отже,
[math]\sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y_i})^2 = \sum_{j=1}^n \sum_{i=1}^m (y_{ij} - \overline{y})^2 + \sum_{j=1}^n \sum_{i=1}^m (\overline{y_i} - \overline{y})^2[/math],
що й треба було довести, оскільки [math]S^2_y \approx \sum \sum (y_{ij} - \overline{y})^2[/math]; [math]S^2_{y/x} \tilde \sum \sum (y_{ij} - \overline{y_i})^2[/math]; [math]S^2_{y/z} \approx \sum \sum (\overline{y_i} - \overline{y})^2[/math].
Другий доданок в здобутому результаті містить тільки одну змінну [math]y_i[/math], яка підсумовується за [math]m[/math] . Тому підсумовування за змінною [math]j[/math] сталою [math](\overline{y_i} - \overline{y})^2[/math] рівнозначне помноженню на [math]n[/math], тобто [math]\sum_{j=1}^n = n[/math], тоді [math]\sum_{j=1}^n \sum_{i=1}^m = (\overline{y_i} - \overline{y})^2 = \sum_{i=1}^m n (\overline{y_i} - \overline{y})^2[/math].
Така сума називається зваженою, оскільки [math]n[/math] у загальному випадку для кожного [math]i[/math] може бути різними.
При використанні дисперсійного аналізу запишемо останні формули через вихідні значення [math]y_{ij}[/math]: [math]\sum \sum (y_{ij} - \overline{y})^2 = \sum \sum y^2_{ij} + \sum \sum \overline{y^2} + 2 \sum \sum y_{ij} \overline{y} =[/math] [math]\sum \sum y_{ij}^2 + m n \overline{y^2} - 2 m n y^2 = \sum \sum y^2_{ij} - m n \overline{y^2} =[/math] [math]\sum \sum y_{ij}^2 - \frac{\mathrm mn}{\mathrm m^2 n^2}\, (\sum \sum y_{ij})^2 = \sum_{j=1}^n \sum_{i=1}^m y^2_{ij} - \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2[/math]; [math]\sum \sum (\overline{y_i} - \overline{y})^2 - \sum^n \sum^m \overline{y^2_i} + \sum^n \sum^m \overline{y^2} - 2\sum^n \sum^m \overline{y_i} \overline{y} =[/math] [math]\sum^n \sum^m y^2_i + \frac{\mathrm mn}{\mathrm m^2 n^2}\, (\sum \sum y_{ij})^2 - 2 m \overline{y} n \overline{y} =[/math] [math]\sum^2 n \frac{\mathrm 1}{\mathrm n^2}\, (\sum^n y_{ij})^2 + \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 - 2 \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2 =[/math] [math]= \frac{\mathrm 1}{\mathrm n}\, \sum^m (\sum^n y_{ij})^2 - \frac{\mathrm 1}{\mathrm mn}\, (\sum \sum y_{ij})^2[/math];
[math]\sum \sum (y_{ij} - \overline{y_i})^2 = \sum \sum y^2_{ij} + \sum \sum \overline{y^2_i} - 2 \sum \sum y_{ij} \overline{y_i} =[/math] [math]\sum^m \sum^n y^2_{ij} + n\sum^m y^2_i - 2\sum^m \sum^n y_{ij} \frac{\mathrm 1}{\mathrm n}\, \sum^n y_{ij} =[/math] [math]\sum \sum y^2_{ij} +n \sum^m \frac{\mathrm 1}{\mathrm n^2}\, (\sum^n y_{ij})^2 - 2\sum^m \frac{\mathrm 1}{\mathrm n}\, (\sum^n y_{ij})^2 =[/math] [math]\sum \sum y^2_{ij} - \frac{\mathrm 1}{\mathrm n}\, \sum^m (\sum^n y_{ij})^2[/math].
Ці формули є робочими при одно факторному дисперсійному аналізі. Якщо розглядати дисперсії не функції, а не залежного параметра, а замість [math]y[/math] покласти [math]x[/math], то структура формул зберігатиметься.
Посилання
В.О. АНІСТРАТЕНКО, В.Г. ФЕДОРОВ. Математичне планування експериментів в АПК: Навч. посібник. - К.: Вища шк., 1993. - 375 с.: іл.