Відмінності між версіями «Сфери застосування планування експерементів»
| (Не показані 5 проміжних версій 4 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name=Андрій | Surname=Бурак | FatherNAme=Михайлович|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
[http://elartu.tstu.edu.ua/handle/123456789/405] Презентація доповіді (університетський репозиторій). | [http://elartu.tstu.edu.ua/handle/123456789/405] Презентація доповіді (університетський репозиторій). | ||
| Рядок 23: | Рядок 24: | ||
Намагаючись дістати якомога точніші результати вимірювання, дослідник має усвідомлювати, що похибки вимірювання є органічними, неусувними властивостями самого процесу вимірювання. Тому моделі, що перевіряються на практиці, мають не тільки бути гіпотезами про досліджуваний об’єкт, а й ураховувати гіпотези щодо точності вхідної інформації. | Намагаючись дістати якомога точніші результати вимірювання, дослідник має усвідомлювати, що похибки вимірювання є органічними, неусувними властивостями самого процесу вимірювання. Тому моделі, що перевіряються на практиці, мають не тільки бути гіпотезами про досліджуваний об’єкт, а й ураховувати гіпотези щодо точності вхідної інформації. | ||
| − | Хоча для проведення експерименту необхідна модель відповідного об’єкта, а для уточнення моделі об’єкта необхідний експеримент, тут немає хибного кола: після завершення чергового циклу наступний починається з нової, зміненої моделі. Ми починаємо з найпростішої моделі вхід—вихід («чорної скриньки») і намагаємось побудувати модель «білої скриньки». | + | Хоча для проведення експерименту необхідна модель відповідного об’єкта [http://metallkovka.com.ua/<span style="color:black;font-weight:normal; text-decoration:none!important; background:none!important; text-decoration:none;">художественная ковка</span>] |
| + | , а для уточнення моделі об’єкта необхідний експеримент, тут немає хибного кола: після завершення чергового циклу наступний починається з нової, зміненої моделі. Ми починаємо з найпростішої моделі вхід—вихід («чорної скриньки») і намагаємось побудувати модель «білої скриньки». | ||
Можна виокремити два основні напрямки в теорії планування експериментів: планування екстремальних експериментів та планування експериментів зі з’ясування механізмів явищ. | Можна виокремити два основні напрямки в теорії планування експериментів: планування екстремальних експериментів та планування експериментів зі з’ясування механізмів явищ. | ||
| Рядок 162: | Рядок 164: | ||
[[Категорія:Виступ на семінарі]] | [[Категорія:Виступ на семінарі]] | ||
[[Категорія:Планування експеримента]] | [[Категорія:Планування експеримента]] | ||
| − | |||
Поточна версія на 10:06, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Андрій | |
| Прізвище | Бурак | |
| По-батькові | Михайлович | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
[1] Презентація доповіді (університетський репозиторій).
Зміст
ВСТУП.
Класичне уявлення про експерименти.
Незважаючи на велике значення експерименту в науковому пізнанні, не існує єдиного загальновизнаного визначення відповідного терміна (це саме стосується, як уже зазначалося й інших фундаментальних понять кібернетики — «система», «модель», «інформація», «управління»). Як правило, під експериментом розуміють створення деякого комплексу умов R, в результаті яких можуть відбуватись чи не відбуватись події з деякої заданої множини S. Предметом теорії експерименту є вивчення відображення цієї множини R, яка називається комплексом умов, на множину S подій — результатів експерименту.
Наведемо ще кілька класичних інтуїтивних визначень.
Експеримент (від лат. experimentum — проба, досвід) — науково поставлене випробування, спостереження досліджуваного явища за певних фіксованих умов, завдяки чому його можна відтворити повторенням цих умов.
Експеримент — випробування, дія чи операція, спрямована на виявлення нових фактів або на перевірку гіпотез.
Зупинимося на деяких аспектах сучасного розуміння експерименту.
Нині вже усвідомлено той факт, що існують явища, які не піддаються числовому (кількісному) вимірюванню, але які можна фіксувати в «слабких», «якісних» шкалах і ці результати враховувати в моделях, дістаючи якісні, проте цілком обґрунтовані висновки.
Розпливчастість деяких спостережень визнається як їхня невід’ємна природна властивість, яку можна математично формалізувати за допомогою апарату теорії нечітких множин.
Намагаючись дістати якомога точніші результати вимірювання, дослідник має усвідомлювати, що похибки вимірювання є органічними, неусувними властивостями самого процесу вимірювання. Тому моделі, що перевіряються на практиці, мають не тільки бути гіпотезами про досліджуваний об’єкт, а й ураховувати гіпотези щодо точності вхідної інформації.
Хоча для проведення експерименту необхідна модель відповідного об’єкта художественная ковка , а для уточнення моделі об’єкта необхідний експеримент, тут немає хибного кола: після завершення чергового циклу наступний починається з нової, зміненої моделі. Ми починаємо з найпростішої моделі вхід—вихід («чорної скриньки») і намагаємось побудувати модель «білої скриньки».
Можна виокремити два основні напрямки в теорії планування експериментів: планування екстремальних експериментів та планування експериментів зі з’ясування механізмів явищ.
Завдання екстремального експерименту полягає у визначенні оптимальних значень функції регресії (чи комбінації факторів, за яких функція відгуку набуває екстремальних значень). Методи планування такого експерименту тісно пов’язані з регресійним та факторним аналізом і методами стохастичного програмування.
У плануванні експериментів зі з’ясування механізмів явищ розрізняють:
• експерименти з перевірки статистичних гіпотез;
• експерименти, що відсіюють другорядні та незначущі фактори;
• імітаційні експерименти, які пов’язані з комп’ютерним відтворенням досліджуваного явища. Цей тип експериментів базується на застосуванні методу Монте-Карло.
Особливості проведення експериментів в економіці.
При дослідженні відносно простих систем дослідник може з достатнім ступенем точності стабілізувати (зафіксувати) усі незалежні змінні. Потім, по черзі варіюючи деякі з них, можна встановити вигляд функціональної (статистичної) залежності між ними. Що ж до економіки, то варто звернути увагу на такі її особливості як об’єкта моделювання.
1. В економіці неможливі моделі за принципом подібності, широко застосовувані в техніці. Наприклад, у літакобудуванні, гідротехніці часто використовується такий прийом: будується точна копія (макет) системи (у деякому масштабі) і на цій копії відпрацьовуються з необхідним коригуванням усі режими її роботи. Однак такий прийом неприйнятний щодо економіки — не можна побудувати точну копію економіки і на ній відпрацювати різні варіанти економічної політики.
2. В економіці обмежена можливість проведення прямих (активних) експериментів. Прямі експерименти з економікою мають як позитивний, так і негативний бік. Перевага таких експериментів полягає в тому, що практично відразу виявляються короткострокові результати здійснюваної економічної політики, а недолік — в тому, що неможливо безпосередньо передбачати середньо- та довгострокові наслідки прийнятих рішень. Адже передбачати такі наслідки можна лише на основі концептуальних моделей розвитку економіки, що спираються на минулий досвід. Проте прямі експерименти з економікою вкрай небезпечні, оскільки в разі невдалої та неефективної економічної політики вони можуть призвести до стагнації економіки та негативних соціальних наслідків.
3. В економіці можливості «чистих» експериментів вельми обмежені, оскільки економічні системи належать до класу великих складних динамічних систем, в яких існують численні контури прямих і зворотних зв’язків. У таких системах не можна встановити «непроникні перегородки», що розмежовують вплив різних факторів. Такі системи називають «погано організованими», або дифузійними.
З огляду на сказане, досліджуючи економіку будь-якої країни, спираються на її минулий досвід та досвід інших країн. Такий досвід важко переоцінити, але далеко не завжди його можна безпосередньо перенести в умови конкретної економічної ситуації. Проте, зважаючи на вельми обмежену можливість безпосереднього експериментування з усією економікою, вдаються до концептуальних моделей, на яких ґрунтується побудова ЕММ. Адекватність таких моделей встановлюється за допомогою сучасної теорії планування (імітаційних) експериментів.
Приклади планування експериментів в медицині та сільському господарстві.
Доволі часто виникає необхідність у визначенні частоти випадків одужання після якогось захворювання - або при випробуванні того чи іншого препарату, або при порівнянні ефективності двох препаратів. Чудова особливість такого статистичного аналізу полягає в тому, що всі види неминучої природної мінливості, що становить як би "фон", на якому виявляється мінливість, пов'язана з досліджуваним фактором, що враховуються в комплексі шляхом використання відповідного розподілу ймовірностей. Якщо фонова мінливість дуже велика, то для отримання остаточних результатів може знадобитися дуже велике число спостережень, а коли вона порівняно мала, результат буде отримано значно швидше.
Якщо який-небудь ефект викликається дуже великим числом різних факторів, то цілком можливо, що фонова мінливість буде вельми велика. У таких випадках доцільно спробувати виділити деякі з цих факторів, навіть якщо їх неможливо повністю контролювати або виключити. Часто виявляється можливим розбити загальну мінливість на окремі компоненти, з яких один відповідає досліджуваного фактору, кілька інших - інших дій, які припускають можливість роздільної оцінки, і останній - інших дій, роздільна оцінка яких неможлива. Оскільки вплив останньої групи чинників, безумовно, буде слабшим, ніж вплив досліджуваного фактора, то це забезпечує більш точну статистичну перевірку.
Мистецтво розташовувати спостереження в певному порядку або проводити спеціально сплановані перевірки з метою повного використання можливостей цих методів і складає зміст предмета "планування експерименту". Тут наведені лише деякі основні переваги свідомого та продуманого планування експерименту.
Перший приклад. Потрібно порівняти болезаспокійливу дію двох різних лікарських препаратів А та В. Нехай підібрано 16 хворих і прийнято рішення розділити їх випадковим чином (щоб уникнути будь-якої свідомо чи мимоволі вноситься систематичної помилки) на дві групи, по 8 хворих в кожній . Одна група отримує препарат А, а інша - препарат В. Потім вимірюють час, протягом якого кожен з хворих відчуває полегшення, і порівнюють середні значення по обох групах. Якщо середній час для препарату А значимо перевищує середній час для препарату В, то можна зробити висновок, що перший препарат більш ефективний. (В даному випадку несуттєво, який статистичний критерій використовується. Оскільки розглядається невелика кількість об'єктів, це може бути один з критеріїв Стьюдента.)
Відомо, що хворі по-різному реагують на один і той самий лікарський препарат, тому тривалість періоду полегшення зазвичай сильно варіює, що значно знижує точність порівняння цих двох препаратів. Проте в даному експерименті відмінності між хворими не становлять для нас особливого інтересу, і це джерело похибки можна виключити такий спосіб. Замість того щоб ділити хворих на дві групи, перевіряють на кожному з них обидва препарати, призначаючи їх послідовно через досить великі проміжки часу (щоб уникнути взаємодії) і у випадковому порядку (або, можливо, в одному порядку для однієї половини хворих і в іншому порядку для іншої).
Тепер для кожного хворого визначають відносну перевагу препарату А перед препаратом В, для чого обчислюють сумарну тривалість періоду полегшення для кожного з них і знаходять різницю цих двох величин. Таким чином отримують 16 чисел, що характеризують відносну перевагу одного препарату перед іншим, що дозволяє перевірити, чи значимо відрізняється від нуля їх середнє значення. Позитивна різниця tA-tB свідчить про статистично значущу перевагу препарату А, негативна - про зворотне співвідношення. Розглядаючи показники відносної переваги, ми виключаємо вплив реакції окремих хворих і в загальному випадку добиваємося більш ефективного порівняння цих двох ліків.
Така проста перевірка методом попарного порівняння являє собою найпростіший план експерименту, який має на меті отримати максимальну кількість інформації з даного числа спостережень. Зауважимо, що цей план має і свої додаткові особливості, тому що вимагає особливої уваги до низки практичних питань, наприклад до того, щоб препарати призначалися у випадковому порядку (щоб уникнути небажаної систематичної помилки) і через досить великі проміжки часу (для виключення ефектів взаємодії) ; однак тут ми не можемо детально розглядати ці питання.
Ми показали, яким чином під час перевірки методом попарного порівняння можна контролювати або виключати з розгляду будь-яке одне важливе і явне джерело мінливості. У більш загальному випадку можуть бути сплановані факторні експерименти, за допомогою яких можна визначити внесок кожного з кількох факторів в загальну мінливість. Деякі з цих факторів можуть становити особливий інтерес, тоді як інші мають другорядне значення. Ідея та практичне застосування цього нового підходу, що належить головним чином Р. Фішером, набули широкого поширення після появи його книги "Планування експериментів", що вийшла першим виданням в 1935 р.
Більшість фундаментальних робіт в області планування експерименту було присвячено сільськогосподарським додаткам. Другий приклад. Припустимо, потрібно зрівняти середню врожайність кількох сортів пшениці при застосуванні різних добрив в різної концентрації, враховуючи при цьому коливання в родючості грунту на досить великих ділянках землі, які можна розбити на ділянки відповідних розмірів. Для початку можна спробувати скласти план експерименту, в якому будуть розглядатися всі можливі комбінації значень, або рівнів, різних факторів. Так, якщо є чотири сорти пшениці і три різних види добрив, що застосовуються в трьох різних концентраціях, то загальна кількість комбінацій умов дорівнюватиме 36. Таким чином, вихідне число ділянок в одному блоці факторного експерименту буде дорівнює 36 - по одній ділянці на кожну комбінацію умов. Внаслідок можливого коливання в родючості грунту від одного блоку до іншого може виявитися доцільним мати не менше двох повних блоків.
Проводиться застосування факторного плану замість класичної схеми, згідно з якою кожен раз змінюється тільки один фактор, що має ряд серйозних і навіть кілька несподіваних переваг. Перш за все в цьому випадку найбільш повною є картина впливу кожного фактора, оскільки воно вивчається в самих різних умовах (внаслідок одночасної зміни інших факторів). По-друге, велика кількість комбінацій факторів, що використовуються в експерименті, полегшує передбачення результатів, які можуть бути досягнуті при певній комбінації умов. По-третє, якщо ефекти, що викликаються кожним фактором, включених в експеримент, статистично незалежні, то про кожному факторі можна отримати не менше інформації, ніж якщо б у процесі експерименту змінювався тільки один цей чинник, а інші залишалися постійними. По-четверте, якщо (як це часто буває) різні фактори не є незалежними, а викликають ефекти, які більшою чи меншою мірою корельовані, то в цьому випадку тільки факторний експеримент може дати інформацію про характер цих взаємодій. За наявності декількох взаємопов'язаних істотних факторів обійтися без постановки факторного експерименту неможливо. Для ряду часто зустрічаються спеціальних завдань розроблено велику кількість стандартних планів такого типу.
Згідно з деякими з цих найпростіших планів, експеримент проводять на декілька блоків і всередині кожного з них на окремих ділянках перевіряють вплив усіх рівнів якогось одного фактора. При правильному плануванні отримують рандомізований блочний план. У сільськогосподарських задачах блоками можуть служити ділянки землі на різних полях, а рівнями одного фактора - ступінчаста послідовність концентрацій добрив або просто різні сорти пшениці. У лабораторному експерименті, в якому, скажімо, перевіряється вплив різних раціонів харчування на щурів, раціони харчування будуть випробовуватись умовами, а щури - окремими експериментальними одиницями (відповідними ділянках в сільськогосподарському експерименті). У розглянутої вище простій перевірці методом попарного порівняння також можна було б застосувати рандомізований блочний план; тоді кожного хворого можна було б розглядати як окремий блок, а лікарські препарати - як умови експерименту.
Логічна схема.
Хоча іноді буває важко перенести плани експериментів, розроблені для однієї області, особливо для сільського господарства, у зовсім іншу область, що лежить в їх основі логічна схема часто опиняється досить сприятливою. Тому доцільно ретельно обміркувати можливість того, щоб при належноій інтерпретації елементів якого-небудь певного плану експерименту можна було б забезпечити його успішне застосування в задачах зовсім іншого характеру. Це ілюструє великі можливості математичних методів планування експерименту. В основі планування повинна, зрозуміло, лежати деяка вихідна математична модель. Опишемо найпростішу з них, яка в тому чи іншому варіанті використовується найбільш широко. Хай потрібно досліджувати вплив тільки двох факторів А та В. Припустимо, що спостерігається на деякій експериментальної одиниці вплив i-го рівня фактора А і j-го рівня фактора В можна записати у вигляді
де[math]yij[/math] – досліджувана величина, m – загальне середнє, [math]ai[/math] і [math]bj[/math] - відносні вклади цих двох чинників при заданих рівнях кожного з них, a [math]zij[/math] - випадкова зміна, що накладається на основну лінійну адитивну схему. Крім того, часто приймається, що всі величини мають один і той же нормальний розподіл і незалежні один від одного.
Ці обмеження досить серйозні, проте часто прийняття їх в якості першого наближення цілком виправдано. Так, якщо вплив цих факторів малий, то помітну величину будуть мати тільки лінійні члени та можливими членами другого порядку можна знехтувати. При незалежності факторів формула (1.1) цілком задовільна. Але якщо вони взаємодіють один з одним, то слід включити в неї додаткові члени сij, що враховують цю взаємодію. Можна, однак, виконати перевірку значущості на основі формули (1.1), щоб переконатися, чи потрібні члени, що характеризують взаємодію. Крім того, якщо випадкові величини zij не розподілені за нормальним законом, то можна використовувати будь-яку функцію емпіричних результатів (наприклад, квадратні корені або логарифми), для якої зберігається нормальний закон розподілу.
На основі елементарної формули (1.1) легко побудувати моделі, що враховують безліч чинників, блоків, взаємодій і інших ускладнень, спричинених практичною необхідністю в кожному даному експерименті. Справа в тому, що в дуже багатьох випадках необхідні обчислення відносно прості і виконуються безпосередньо. Зазвичай доводиться виробляти повторювані обчислення сум і сум квадратів даних, обраних відповідним чином. Результати представляють у вигляді таблиці дисперсійного аналізу, за допомогою якої можна встановити значимість всіх різних факторів, що впливають на результати експерименту.
Послідовна схема.
Одним із сучасних варіантів планування експериментів, який слід розглянути окремо, є послідовна схема експерименту. В експерименті стандартного типу необхідно заздалегідь вирішити, скільки спостережень потрібно набрати. Якщо після аналізу виявиться, що кількість спостережень занадто мало, то потрібно спробувати продовжити експеримент, однак може виявитися, що на даному етапі зробити це важко або неможливо. Якщо ж з'ясується, що отримано значно більше спостережень, ніж необхідно для досягнення необхідної точності, то буде втрачено час і гроші. У медичних задачах це має особливо істотне значення. Жоден лікар не зацікавлений в тому, щоб експеримент тривав довше, ніж це строго необхідно, тому що його мета - дати своїм хворим найкращий з існуючих препаратів, як тільки він пройде клінічні випробування. Таким чином, в медицині вибір і планування експерименту найтіснішим чином пов'язані з етичними міркуваннями.
Послідовна схема передбачає проведення експерименту окремими серіями. Оцінка результатів проводиться на кожному етапі, з тим щоб негайно можна було вирішити, застосовувати препарат А, препарат В або ж продовжувати експеримент, оскільки остаточного висновку зробити ще не можна. За такої схеми експерименту тривалість його буде мінімальна і він закінчиться значно раніше, ніж у будь-якому іншому випадку. Крім того, в медицині часто буває дуже важко або навіть взагалі неможливо провести звичайну експериментальну перевірку, тому що після кількох невдалих результатів, які можуть закінчитися смертю хворого, починаються гострі суперечки про те, чи варто продовжувати експеримент взагалі. Послідовних схема означає, що заздалегідь можна ретельно і спокійно розглянути різні лінії поведінки, зумовлюється різними результатами експерименту. При цьому значно легше вибрати найкращі рішення безпосередньо в ході експерименту і сумістити вимоги етики з статистичною ефективністю.
Приклад застосування в хімії.
Розрахунок швидкості корозії.
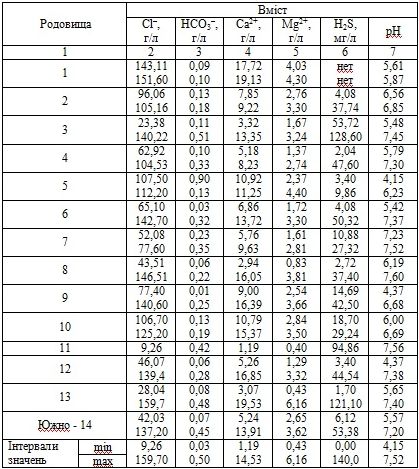
Розрахунок швидкості корозії в промислових водах проводиться з метою оцінки корозійної характеристики середовища за змістом корозійно-активних компонентів. Згідно з РД 39-0147323-339-89-Р основними корозійно-активними складовими промислових вод є рН, HCO3-, Cl-, Ca2 +, Mg2 +, H2S. Оскільки рН є похідним від змісту HCO3-, H2S і вплив іонів Ca2 + і Mg2 + аналогічно, були взяті чотири складові - HCO3-, Cl-, Ca2 + + Mg2 +, H2S.
На першому етапі роботи була зібрана апріорна інформація за даними складу промислових вод за період з 1995 по 1999 роки по родовищах (таблиця 1). Джерелом інформації служили результати аналізів промислових вод, проведені хіміко-аналітичною лабораторією за період часу. Найбільш істотним в таблиці є мінімальне та максимальне утримання кожного компонента. Як фактори були взяті:
х1 - вміст HCO3-, г / л;
х2 - вміст Ca2 + + Mg2 +, г / л;
х3 - вміст Cl-, г / л;
х4 - вміст H2S, мг / л.
Таблиця 1 - Зміна змісту корозійно-активних компонентів в стічній воді по родовищах за 1995-1999 роки
У ході дослідження важливим було відстеження взаємодії факторів. Виходячи з цього, було прийнято математичний опис процесу у вигляді рівняння регресії для чотирьох змінних:
[math]vcor = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b11x12 + b22x22 + b33x33 + b44x44 + b12x1x2 + B13x1x3 + b14x1x4 + b23x2x3 + b24x2x4 + b34x3x4.[/math]
Використання в якості моделі полінома другого порядку вимагає варіювання факторів на п'яти рівнях. Відповідно до апріорної інформацією були прийняті значення рівнів, представлені в таблиці 2.
Таблиця 2 - Значення рівнів варіювання факторів.
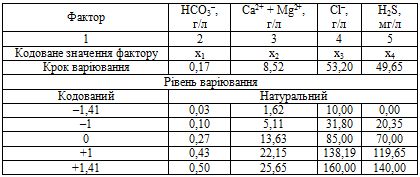
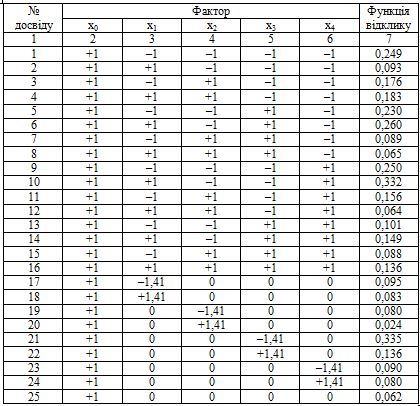
Так як в якості моделі взяли поліном другого порядку для розрахунку коефіцієнтів зручно скористатися методом центрального композиційного планування (ЦКОП). В основному експерименті в центрі плану передбачався один досвід, тому значення «зоряного» плеча α береться рівним +1. Кількість експериментів рівне 25. З огляду на вимоги, які розглядаються, була складена матриця планування в умовному масштабі. При проведенні основного експерименту досліди були рандомізовані.
Таблиця 3 - Матриця планування чотирьохфакторного експерименту.
Коррозия и защита в нефтегазовой промышленности: Экономическая эффективность катодной защиты обсадных колонн скважин / Под ред. Г.С. Кесельмана, В.Б. Максимова. - М.: ВНИИОЭНГ, 1974. - 74 с. http://nature.web.ru/db/msg.html?mid=1156624&uri=2_3.htm http://buklib.net/component/option,com_jbook/task,view/Itemid,36/catid,128/id,3694/
Список використаних джерел
- Коррозия и защита в нефтегазовой промышленности: Экономическая эффективность катодной защиты обсадных колонн скважин / Под ред. Г.С. Кесельмана, В.Б. Максимова. - М.: ВНИИОЭНГ, 1974. - 74 с.
- http://nature.web.ru/db/msg.html?mid=1156624&uri=2_3.htm;
- http://buklib.net/component/option,com_jbook/task,view/Itemid,36/catid,128/id,3694.

- Студент: Користувач:zvizdar
- Виступ відбувся: 8 березня 2010
- Тема: Приклади задач у народному господарстві, в тому числі у багатьох областях медицини та ін.