Відмінності між версіями «Прогнозування за допомогою нейронних мереж»
| (Не показано 4 проміжні версії 2 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| + | {{Студент | Name=Юля | Surname=Чорнописька | FatherNAme=|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | ||
[http://elartu.tstu.edu.ua/handle/123456789/401] Презентація доповіді (університетський репозиторій). | [http://elartu.tstu.edu.ua/handle/123456789/401] Презентація доповіді (університетський репозиторій). | ||
| Рядок 296: | Рядок 297: | ||
[[Категорія:ПЕ-2010]] | [[Категорія:ПЕ-2010]] | ||
[[Категорія:Виступ на семінарі]] | [[Категорія:Виступ на семінарі]] | ||
| − | [[Категорія:Планування | + | [[Категорія:Планування експеримента]] |
| − | |||
| − | |||
Поточна версія на 10:01, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Юля | |
| Прізвище | Чорнописька | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
[1] Презентація доповіді (університетський репозиторій).
Зміст
Означення нейронної мережі
Штучні нейронні мережі (ШНМ) – математичні моделі, а також їх програмні або апаратні реалізації, побудовані за принципом організації й функціонування біологічних нейронних мереж – мереж нервових кліток живого організму. Це поняття виникло при вивченні процесів, що протікають у мозку, і при спробі змоделювати ці процеси. Першою такою спробою були нейронні мережі Маккалока й Піттса. Згодом, після розробки алгоритмів навчання, одержувані моделі стали використовувати в практичних цілях: у завданнях прогнозування, для розпізнавання образів, у завданнях керування й ін.
ШНМ являють собою систему з'єднаних і взаємодіючих між собою простих процесорів (штучних нейронів). Такі процесори звичайно досить прості, особливо в порівнянні із процесорами, використовуваними в персональних комп'ютерах. Кожний процесор подібної мережі має справу тільки із сигналами, які він періодично одержує, і сигналами, які він періодично посилає іншим процесорам. Проте, з'єднавши їх в досить велику мережу з керованою взаємодією, такі локально прості процесори разом здатні виконувати досить складні завдання. З погляду машинного навчання, нейронна мережа являє собою окремий випадок методів розпізнавання образів, методів кластеризації й т.п. З математичної точки зору, навчання нейронних мереж – це багатопараметричне завдання нелінійної оптимізації. З погляду кібернетики, нейронна мережа використовується в завданнях адаптивного керування і як алгоритми для робототехніки. З погляду розвитку обчислювальної техніки й програмування, нейронна мережа – спосіб розв'язку проблеми ефективного паралелізму. А з погляду штучного інтелекту, ИНС є основним напрямком у структурному підході по вивченню можливості побудови (моделювання) природнього інтелекту за допомогою комп'ютерних алгоритмів.
Нейронні мережі не програмуються у звичному змісті цього слова, вони навчаються. Можливість навчання – одне з головних переваг нейронних мереж перед традиційними алгоритмами. Технічно навчання полягає в знаходженні коефіцієнтів зв'язків між нейронами. У процесі навчання нейронна мережа здатна виявляти складні залежності між вхідними даними й вихідними, а також виконувати узагальнення. Це значить, що, у випадку успішного навчання, мережа зможе повернути вірний результат на підставі даних, які були відсутні в навчальній вибірці, а також неповних і/або «зашумлених», частково перекручених даних.
Біологічний нейрон
Нейрон (нервова клітка) складається з тіла клітини –соми (soma, cell body), і двох типів зовнішніх деревоподібних відгалужень: аксона (axon) і дендритів (dendrites). Тіло клітини вміщує ядро (nucleus), що містить інформацію про властивості нейрона, і плазму, яка продукує необхідні для нейрона матеріали. Нейрон отримує сигнали (імпульси) від інших нейронів через дендрити (приймачі) і передає сигнали, згенеровані тілом клітки, вздовж аксона (передавач), що наприкінці розгалужується на волокна (strands). На закінченнях волокон знаходяться синапси (synapses).
Рисунок 1. – Схема біологічного нейрона
Синапс є функціональним вузлом між двома нейронами (волокно аксона одного нейрона і дендрит іншого). Коли імпульс досягає синаптичного закінчення, продукуються хімічні речовини, названі нейротрансмітерами. Нейротрансмітери проходять через синаптичну щілину, збуджуючи або гальмуючи, у залежності від типу синапсу, здатність нейрона-приймача генерувати електричні імпульси. Результативність синапсу налаштовується минаючими через нього сигналами, тому синапси навчаються в залежності від активності процесів, у яких вони приймають участь. Нейрони взаємодіють за допомогою короткої серії імпульсів. Повідомлення передається за допомогою частотно-імпульсної модуляції.
Структура штучного нейрона
Нейрон є складовою частиною нейронної мережі. На рисунку 2.1 представлена його структура. Він складається з елементів трьох типів: помножувачів (синапсів), суматора і нелінійного перетворювача. Синапси здійснюють зв’язок між нейронами, множать вхідний сигнал на число, що характеризує силу зв’язку, (вагу синапса). Суматор виконує додавання сигналів, що надходять по синаптичним зв’язках від інших нейронів і зовнішніх вхідних сигналів. Нелінійний перетворювач реалізує нелінійну функцію одного аргументу – виходу суматора. Ця функція називається функцією активації чи передатною функцією нейрона.
Рисунок 2. – Структура штучного нейрона
Архітектура нейронної мережі
Існуючі на даний час, нейромережі є групуванням штучних нейронів. Це групування обумовлено створенням з'єднанних між собою прошарків. На рис. 3 показана типова структура штучних нейромереж. Хоча існують мережі, які містять лише один прошарок, або навіть один елемент, більшість застосувань вимагають мережі, які містять як мінімум три нормальних типи прошарків – вхідний, прихований та вихідний. Прошарок вхідних нейронів отримує дані або з вхідних файлів, або безпосередньо з електронних давачів. Вихідний прошарок пересилає інформацію безпосередньо до зовнішнього середовища, до вторинного комп'ютерного процесу, або до інших пристроїв. Між цими двома прошарками може бути багато прихованих прошарків, які містять багато нейронів у різноманітних зв'язаних структурах. Входи та виходи кожного з прихованих нейронів просто йдуть до інших нейронів.
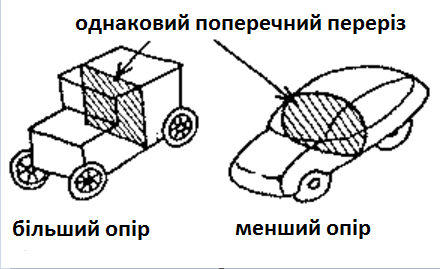
Рисунок 3. – Діаграма простої нейронної мережі
Напрямок зв'язку від одного нейрону до іншого є важливим аспектом нейромереж. У більшості мереж кожен нейрон прихованого прошарку отримує сигнали від всіх нейронів попереднього прошарку та звичайно від нейронів вхідного прошарку. Після виконання операцій над сигналами, нейрон передає свій вихід до всіх нейронів наступних прошарків, забезпечуючи шлях передачі вперед (feedforward) на вихід. Багатошарові нейронні мережі можна поділити на: - мережі прямого розповсюдження ; - мережі зі зворотними зв’язками. У мережах прямого розповсюдження нейрони вхідного шару отримають вхідні сигнали, перетворюють і передають їх нейронам першого шару, останні – нейронам другого, потім третього і так дальше аж до вихідного шару, який видає їх користувачу. У мережах зі зворотними зв’язками інформація з подальших шарів передається на попередні.
Навчання штучної нейронної мережі
Здатність до навчання є фундаментальною властивістю мозку. Процес навчання може розглядатися як визначення архітектури мережі і налаштування ваг зв'язків для ефективного виконання спеціальної задачі. Нейромережа налаштовує ваги зв'язків по наявній навчальній множині. Властивість мережі навчатися на прикладах робить їх більш привабливими в порівнянні із системами, які функціонують згідно визначеній системі правил, сформульованої експертами.
Для процесу навчання необхідно мати модель зовнішнього середовища, у якій функціонує нейронна мережа – потрібну для вирішення задачі інформацію. По-друге, необхідно визначити, як модифікувати вагові параметри мережі. Алгоритм навчання означає процедуру, в якій використовуються правила навчання для налаштування ваг.
Існують три загальні парадигми навчання: "з вчителем", "без вчителя" (самонавчання) і змішана.
У першому випадку нейромережа має у своєму розпорядженні правильні відповіді (виходи мережі) на кожен вхідний приклад. Ваги налаштовуються так, щоб мережа виробляла відповіді як можна більш близькі до відомих правильних відповідей.
Навчання "без вчителя" не вимагає знання правильних відповідей на кожен приклад навчальної вибірки. У цьому випадку розкривається внутрішня структура даних та кореляція між зразками в навчальній множині, що дозволяє розподілити зразки по категоріях.
При змішаному навчанні частина ваг визначається за допомогою навчання зі вчителем, у той час як інша визначається за допомогою самонавчання.
У загальному використанні є багато правил навчання, але більшість з цих правил є деякою зміною відомого та найстаршого правила навчання, правила Хеба. Дослідження різних правил навчання триває, і нові ідеї регулярно публікуються в наукових та комерційних виданнях. Представимо декілька основних правил навчання.
Правило Хеба
Опис правила з'явився у його книзі "Організація поведінки" у 1949 р. "Якщо нейрон отримує вхідний сигнал від іншого нейрону і обидва є високо активними (математично мають такий самий знак), вага між нейронами повинна бути підсилена". При збудженні одночасно двох нейронів з виходами (хj, уі) на t-тому кроці навчання вага синаптичного з'єднання між ними зростає, в інакшому випадку - зменшується, тобто
[math]Wij(k)=r xj (k) yi (k)[/math],
де r - коефіцієнт швидкості навчання.
Може застосовуватись при навчанні "з вчителем" і "без вчителя".
Правило Хопфілда
Є подібним до правила Хеба за винятком того, що воно визначає величину підсилення або послаблення. "Якщо одночасно вихідний та вхідний сигнал нейрона є активними або неактивними, збільшуємо вагу з'єднання оцінкою навчання, інакше зменшуємо вагу оцінкою навчання".
Правило "дельта".
Це правило є подальшою зміною правила Хеба і є одним із найбільш загально використовуваних. Це правило базується на простій ідеї неперервної зміни синаптичних ваг для зменшення різниці ("дельта") між значенням бажаного та біжучого вихідного сигналу нейрона.
[math]Wij= xj (di - yi).[/math]
За цим правилом мінімізується середньоквадратична похибка мережі. Це правило також згадується як правило навчання Відрова-Хофа та правило навчання найменших середніх квадратів.
У правилі "дельта" похибка отримана у вихідному прошарку перетворюється похідною передатної функції і послідовно пошарово поширюється назад на попередні прошарки для корекції синаптичних ваг. Процес зворотного поширення похибок мережі триває до досягнення першого прошарку.
При використанні правила "дельта" важливим є невпорядкованість множини вхідних даних. При добре впорядкованому або структурованому представленні навчальної множини результат мережі може не збігтися до бажаної точності і мережа буде вважатись нездатною до навчання.
Правило градієнтного спуску
Це правило подібне до правила "дельта" використанням похідної від передатної функції для змінювання похибки "дельта" перед тим, як застосувати її до ваг з'єднань. До кінцевого коефіцієнта зміни, що діє на вагу, додається пропорційна константа, яка пов'язана з оцінкою навчання. І хоча процес навчання збігається до точки стабільності дуже повільно, це правило поширене і є загально використовуване.
Доведено, що різні оцінки навчання для різних прошарків мережі допомагає процесу навчання збігатись швидше. Оцінки навчання для прошарків, близьких до виходу, встановлюються меншими, ніж для рівнів, ближчих до входу.
Навчання методом змагання
На відміну від навчання Хеба, у якому множина вихідних нейронів може збуджуватись одночасно, при навчанні методом змагання вихідні нейрони змагаються між собою за активізацію. Це явище, відоме як правило "переможець отримує все". Подібне навчання має місце в біологічних нейронних мережах. Навчання за допомогою змагання дозволяє кластеризувати вхідні дані: подібні приклади групуються мережею відповідно до кореляцій і представляються одним елементом.
При навчанні модифікуються синаптичні ваги нейрона-переможця. Ефект цього правила досягається за рахунок такої зміни збереженого в мережі зразка (вектора синаптичних ваг нейрона-переможця), при якому він стає подібним до вхідного приклада. Нейрон з найбільшим вихідним сигналом оголошується переможцем і має можливість гальмувати своїх конкурентів і збуджувати сусідів. Використовується вихідний сигнал нейрона-переможця і тільки йому та його сусідам дозволяється коректувати свої ваги з'єднань.
[math]Wij (k+1)= Wij(k)+r [xj - Wij(k)][/math]
Розмір області сусідства може змінюватись під час періоду навчання. Звичайна парадигма повинна починатись з великої області визначення сусідства і зменшуватись під час процесу навчання. Оскільки елемент-переможець визначається по найвищій відповідності до вхідного зразку, мережі Коxонена моделюють розподіл входів. Це правило використовується в самоорганізованих картах.
Задачі прогнозування
Особливе значення мають задачі передбачення та прогнозування часових рядів, серед яких виділяються завдання з набором певних специфічних ознак, тому варто провести їх класифікацію. Задачі дослідження явищ, розвиток яких пов'язаний із часом, можна поділити на декілька класів:
За характером основних ознак об'єкту:
• прогнозування явищ, реалізації яких представлені у вигляді детермінованих часових рядів. Такі задачі, зокрема, можна вирішити шляхом застосування методів математичного аналізу;
• прогнозування явищ, реалізації яких представлені у вигляді індетермінованих часових рядів. Вирішення цих задач традиційно здійснюється шляхом застосування методів теорії ймовірностей та математичної статистики. Зокрема, реалізації таких явищ, можуть мати вигляд:
а) стаціонарного часового ряду, який характеризується однорідністю в часі, без суттєвих змін характеру коливань та їх середньої амплітуди;
б) нестаціонарного часового ряду, який характеризується певною тенденцією розвитку в часі; при дослідженні нестаціонарних процесів можна виділити ділянки, на яких процес можна вважати стаціонарним; вибір проміжку для формування навчальної множини в такому випадку обирається згідно задачі прогнозування;
За числом ознак об'єкту досліджень:
• одновимірна задача; явище представлене лише однією ознакою, зміни якої відбуваються в часі;
• багатовимірна задача; об'єкт або явище представлені кількома ознаками; задача прогнозування може бути розширена завдяки представленню даних в просторі.
За часом випередження розрізняють види прогнозів:
• згладжування, R= 0;
• короткотерміновий прогноз, R= 1… 2;
• середньотерміновий прогноз, R= 3 … 7;
• довготерміновий прогноз, R= 10 … 15.
Очевидно, що вид прогнозу суттєво впливає на вибір засобів і методику його реалізації.
Загальні підходи до прогнозування за допомогою нейронних мереж
Дані про поведінку об'єкта, ознаки якого пов'язані з часом, представлені як результати спостережень в рівномірні відліки часу. Для моментів часу t=1, 2, ..., n дані спостережень набувають вигляду часового ряду х(t1), х(t2), ..., х(tn). Інформація про значення часового ряду до моменту n дозволяє давати оцінки параметрів x(tn+1), x(n+2), ..., x(n+m). Для здійснення прогнозування елементів часових рядів широко використовують так званий метод "часових вікон".
В залежності від кількості ознак, що представляють значення рядів при формуванні множин даних, виділимо задачі двох типів.
Однопараметрична задача прогнозування
Нехай часовий ряд x(t) задано відліками процесу x(t1), x(t2),..., x(tі) в дискретні моменти часу t. Задамо ширину (кількість дискретних відліків) вхідного часового вікна m, ширину вихідного вікна р. Вхідне та вихідне вікна накладаються на дані ряду, починаючи з першого елемента (рис. 4).
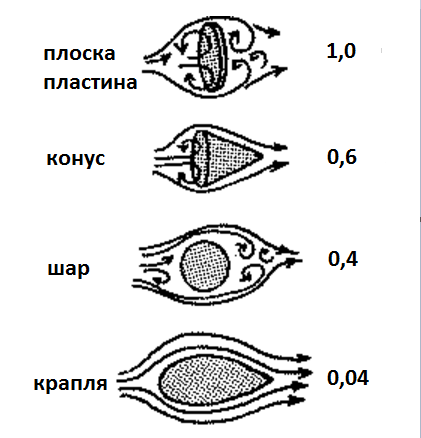
Рисунок 4. – Формування множин даних для однопараметричної задачі за методом "часових вікон"
Вхідне вікно формує дані для входів нейронної мережі, а вихідне, відповідно, для виходів. Подібна пара вхідного та вихідного векторів приймається за одну реалізацію часового ряду. При зсуві часових вікон за часовим рядом з кроком s, отримуємо другу і наступні реалізації.
Значення ширини вікон та кроку зміщення повинні узгоджуватись з особливостями часового ряду, що забезпечується шляхом проведення експериментів. Нехай вхідне вікно має ширину m, вихідне вікно р=1, крок зміщення s=1. Тоді сформована множина значень для однопараметричної задачі матиме вигляд, наведений нижче:
Таблиця 1. – Множина даних для однопараметричної задачі
Багатопараметрична задача прогнозування
В багатопараметричних задачах прогнозування підходи до розв'язання проблеми залишаються подібними (рис.5).
Рисунок 5. – Формування множин даних для багатопараметричної задачі
Нехай потрібно спрогнозувати взаємозалежні величини x(t), y(t), ..., z(t). Якщо прийняти ширину вхідного вікна m, вихідного р=1, кроку зміщення s=1, можна сформувати множину даних наступним чином:
Таблиця 2. – Множина даних для багатопараметричної задачі
Функціонування нейромережі здійснюється у відповідності з показаним методом часових вікон, зберігаючи значення ширини вікон та кроку зсуву. Конкретизація підходів до реалізації прогнозування в значній мірі залежить також від особливостей явища, що досліджується.
Однокрокове прогнозування (передбачення)
Задача однокрокового прогнозування зводиться до задачі відображення, коли один вхідний вектор відображається у вихідний (рис. 6).
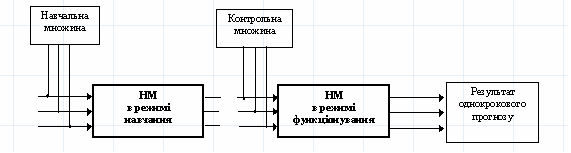
Рисунок 12. – Послідовність використання нейромереж для задач передбачення
У випадку однопараметричної задачі передбачення навчальна множина до моменту n, за умови m=3, p=1, s=1, матиме вигляд наведений в таблиці 3. Таблиця 3. – Навчальна множина для однопараметричної задачі передбачення

В режимі навчання встановлюються коефіцієнти ваг зв'язків, після чого стає можливим перехід до режиму функціонування. Для передбачення на входи нейромережі надходять значення останньої реалізації навчальної множини [math]x(tn-2)[/math], [math]x(tn-1)[/math], [math]x(tn)[/math]. На виході формується прогнозована величина x*(tn+1).
Для багатопараметричної задачі передбачення на входи навченої нейромережі подаються вектори [math]x(tn-2)[/math], [math]y(tn-2)[/math], [math]z(tn-2)[/math], [math]x(tn-1[/math]), [math]y(tn-1)[/math], [math]z(tn-1)[/math], [math]x(tn)[/math], [math]y(tn)[/math], [math]z(tn)[/math]. На виходи нейромережі надходять передбачені величини x*(tn+1), y*(tn+1), z*(tn+1), які відкладаються у вихідний вектор передбачених даних.
Показаний режим є однокроковим, який працює в режимі відображення (реальний вхід®прогнозований вихід). Передбачення застосовують також для моделювання дискретних послідовностей, що не пов'язані з часом. Враховуючи специфіку часових рядів, такий тип прогнозу не завжди є доцільним, але для певних випадків короткотермінових прогнозів ним можливо скористатись.
Багатокрокове прогнозування
Багатокрокове прогнозування застосовують лише для явищ, ознаки яких представлені у вигляді часових рядів.
Для однопараметричної задачі прогнозування навчальна множина матиме вигляд наведений в табл. 3. Під час навчання мережа налаштовує коефіцієнти ваг зв'язків і поліномів передатних функцій, які в подальшому і визначають режим функціонування. Багатокрокове прогнозування часового ряду здійснюється наступним чином (рис. 6). На входи нейромережі подається вектор відомих значень [math]x(tn-2)[/math], [math]x(tn-1)[/math], [math]x(tn)[/math]. На виході формується прогнозована величина [math]x*(tn+1)[/math], яка визначає вектор прогнозованих виходів і одночасно долучається до значень навчальної множини, тобто, приймається як достовірна. Далі на входи подається вектор [math]x(tn-1)[/math], [math]x(tn)[/math], [math]x*(tn+1)[/math], а на виході отримується [math]x*(tn+2)[/math] і наступні прогнозовані значення.
Рисунок 6. – Послідовність використання НМ для задач багатокрокового прогнозування
Для багатопараметричної задачі прогнозування на входи навченої нейромережі подаються вектори [math]x(tn-2)[/math], [math]y(tn-2)[/math], [math]z(tn-2)[/math], [math]x(tn-1)[/math], [math]y(tn-1)[/math], [math]z(tn-1)[/math], [math]x(tn)[/math], [math]y(tn)[/math], [math]z(tn)[/math]. На виході продукуються величини x*(tn+1), y*(tn+1), z*(tn+1), які формують вектор вихідних значень і послідовно долучаються до значень навчальної множини. При зсуві вікна на крок прогнозу вихідні дані, що були спродуковані мережею, сприймаються як реальні і приймають участь у прогнозуванні наступного значення виходу, тобто на входи подаємо вектор [math]x(tn-1)[/math], [math]y(tn-1)[/math], [math]z(tn-1)[/math], [math]x(tn)[/math], [math]y(tn)[/math], [math]z(tn)[/math], [math]x*(tn+1)[/math], [math]y*(tn+1)[/math], [math]z*(tn+1)[/math], а на виході отримуємо x*(tn+2), y*(tn+2), z*(tn+2) і наступні прогнозовані значення.
Багатокрокове прогнозування дозволяє робити коротко- та середньотермінові прогнози, оскільки суттєвий вплив на точність має накопичення похибки на кожному кроці прогнозування. При застосуванні довготермінового багатокрокового прогнозування спостерігається характерне для багатьох прогнозуючих систем поступове затухання процесу, фазові зсуви і інші спотворення картини прогнозу. Такий тип прогнозування підходить для часових рядів, які підпадають під означення стаціонарного процесу з невеликою випадковою складовою.
Багатокрокове прогнозування з перенавчанням нейромережі на кожному кроці прогнозу
Швидкі неітераційні алгоритми навчання дозволяють запропонувати новий тип багатокрокового прогнозу, який може бути застосований при довготермінових прогнозах із збереженням задовільної точності прогнозування. Аналогічно з попереднім алгоритмом прогнозування на входи мережі у режимі функціонування надходить остання реалізація навчальної множини [math]x(tn-2)[/math], [math]x(tn-1)[/math], [math]x(tn)[/math]. Прогнозоване значення виходу [math]x*(tn+1)[/math] відкладається у векторі прогнозованих вихідних значень і в якості достовірного додається до реальних значень навчальної множини. Навчальна множина збільшується на одне часове вікно. Відбувається процес перенавчання мережі на збільшеній навчальній множині, під час якого визначаються нові вагові коефіцієнти k синаптичних зв'язків і поліномів передатних функцій нейронів (рис. 7).

Рисунок 7. – Послідовність використання нейромережі для задач багатокрокового прогнозування з перенавчанням
Реалізація [math]x(tn-1)[/math], [math]x(tn)[/math], [math]x*(tn+1)[/math], як значення наступного вхідного вікна подається на входи мережі в режимі функціонування. Мережа продукує нове вихідне значення [math]x*(tn+2)[/math], яке відповідно також відкладається у вектор продукованих виходів і долучається до реальних значень навчальної множини, з метою подальшого перенавчання мережі та встановлення поновлених коефіцієнтів поліномів передатних функцій і синаптичних зв'язків. Ітераційна процедура перенавчання поширюється до прогнозованого значення [math]x*(tN)[/math].
Такий підхід дозволяє при великих інтервалах випередження усунути затухання прогностичних властивостей мережі за рахунок постійного коректування вагових коефіцієнтів синаптичних зв'язків.
Відзначимо, що алгоритм багатокрокового прогнозування з перенавчанням мережі для традиційних мереж прямого поширення з ітераційним навчанням є практично нездійсненним через великі часові затримки, необхідні на переналаштовування коефіцієнтів мережі.
Нейромережеві моделі бізнес-прогнозування
Зараз, найперспективнішим методом прогнозування є використання нейронних мереж. Можна назвати багато переваг нейронних мереж над іншими алгоритмами, нижче наведено два основні.
При використанні нейронних мереж легко досліджувати залежність прогнозованої величини від незалежних змінних. Наприклад, є припущення, що продажі на наступному тижні якимось чином залежать від наступних параметрів:
• продажів в останній тиждень
• продажів у передостанній тиждень
• часу прокручування рекламних роликів (TRP)
• кількості робочих днів
• температури
Крім того, продажі носять сезонний характер, мають тренд і якось залежать від активності конкурентів.
Хотілося б побудувати систему, яка б усе це природнім чином враховувала і будувала б короткострокові прогнози.
У такій постановці завдання застосування більшої частини класичних методів прогнозування буде просто неможливою.
Використовуючи ж навіть найпростішу нейромережеву архітектуру (перцептрон з одним схованим шаром) і базу даних (із продажами й усіма параметрами) легко одержати працюючу систему прогнозування. Причому враховувати, чи не враховувати зовнішні параметри системою буде визначатися включенням, або виключенням відповідного входу в нейронну мережу.
Експерт може скористатися яким-небудь алгоритмом визначення важливості і відразу визначити значимість вхідних змінних, щоб потім виключити з розгляду параметри, що мають незначний вплив.
Ще одна серйозна перевага нейронних мереж полягає в тому, що експерт не є заручником вибору математичної моделі поведінки часового ряду. Побудова нейромережевої моделі відбувається адаптивно під час навчання, без участі експерта. При цьому нейронній мережі пред'являються приклади з бази даних і вона сама підлаштовується під ці дані.
Недоліком нейронних мереж є їхня недетермінованість. Мається на увазі те, що після навчання є "чорний ящик", який якимось чином працює, але логіка прийняття розв'язків нейромережею зовсім схована від експерта. У принципі, існують алгоритми "витягу знань із нейронної мережі", які формалізують навчену нейронну мережу до списку логічних правил, тим самим створюючи на основі мережі експертну систему. На жаль, ці алгоритми не вбудовуються в нейромережеві пакети, до того ж набори правил, які генеруються такими алгоритмами досить об'ємні.
Проте, для людей, що вміють працювати з нейронними мережами й знаючими нюанси налаштування, навчання й застосування, у практичних завданнях непрозорість нейронних мереж не є настільки серйозним недоліком. Використання багатошарових персептронов
Найпростіший варіант застосування штучних нейронних мереж у завданнях бізнес-прогнозування – використання звичайного перцептрона з одним, двома, або трьома прихованими шарами. При цьому на входи нейронної мережі звичайно подається набір параметрів, на основі якого ( на думку експерта) можна успішно прогнозувати. Виходом звичайно є прогноз мережі на майбутній момент часу.

Розглянемо приклад прогнозування продажів. На малюнку представлений графік, що віддображає історію продажів деякого продукту по тижнях. У даних явно помітна виражена сезонність. Для простоти припустимо, що ніяких інших потрібних даних у нас немає. Тоді мережу логічно будувати в такий спосіб. Для прогнозування на майбутній тиждень треба подавати дані про продажі за останні тижні, а також дані про продажі в плині декількох тижнів підряд рік тому, щоб мережа бачила динаміку продажів один сезон назад, коли ця динаміка була схожа на справжню за рахунок сезонності.
Якщо вхідних параметрів багато, рекомендується не скидати їх відразу в нейронну мережу, а спробувати спочатку провести перед обробку даних, для того щоб понизити їхню розмірність, або представити в правильному виді. У більшості практичних завдань по прогнозуванню продажів перед обробка складається з різних частин. От лише один приклад.
Нехай у попередньому прикладі в нас є не тільки історична база даних про продажі продукту, які ми прогнозуємо, але й дані про його рекламу на телебаченні. Ці дані можуть виглядати в такий спосіб
По осі часу відкладені номери тижнів і рекламні індекси для кожного тижня. Видно, що в шістнадцятому й сімнадцятому тижні реклами не було взагалі. Очевидно, що неправильно дані про рекламу подавати в у такому виді, оскільки визначає продажу не сама реклама як така, а образи й враження у свідомості покупця, які ця реклама створює. І така реклама має тривалу дію - навіть через кілька місяців після закінчення реклами на телебаченні люди будуть пам'ятати продукт і купувати його, хоча, швидше за все, продажу будуть поступово падати. Тому намагаючись подавати в мережу такі дані про рекламу ми робимо неправильну постановку завдання й, як мінімум, ускладнимо мережі процес навчання.
При використанні багатошарових нейронних мереж у бізнес-прогнозуванні в загальному і прогнозуванні продажів зокрема корисно також пам'ятати про те, що потрібно акуратно робити нормування й що для вихідного нейрона краще використовувати лінійну передатну функцію. Узагальнюючі властивості від цього небагато погіршуються, але мережа буде набагато краще працювати з даними, що містять тренд.
Список використаних джерел
- http://masters.donntu.edu.ua/2003/fvti/paukov/library/neurow.htm
- http://victoria.lviv.ua/html/oio/
- Уоссермен Ф.. Нейрокомпьютерна техніка. - М.: Світ, 1992
Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теорія и практика. – М.: Горячая линия - Телеком, 2001. – 382 с.
- Мак-Каллок У. С., Питтс В. Логическое исчисление идей, относящихся к нервной активности // В сб.: «Автоматы» под ред. К. Э. Шеннона и Дж. Маккарти. — М.: Изд-во иностр. лит., 1956. — с.363-384. (Перевод английской статьи 1943 г.).
- http://www.neuroproject.ru/forecasting_tutorial.php#mlp
- Нейронные сети. Саймон Хайкин. – М.: Вильямс, 2006. – 1103

- Студент: Користувач:ulyasi4ka
- Виступ відбувся: 04 березня 2010
- Тема: Прогнозування за допомогою нейронних мереж