Відмінності між версіями «Ядерне згладжуваня»
Vova (обговорення • внесок) (→Принцип) |
Vova (обговорення • внесок) (→Приклад функції ядра) |
||
| (Не показано 27 проміжних версій цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | ''' | + | {{Завдання|Шостак В.М.|Назаревич О. Б.|18 березня 2012}} |
| + | {{Студент | Name=Володимир | Surname=Шостак | FatherNAme=Михайлович |Faculti=ФІС | Group=СН-51 | Zalbook=СН-11-222}} | ||
| + | '''Ядерне згладжуваня''' - один із найпростіших видів [[Непараметрична регресія|непараметричної регресії]]. | ||
| − | == Постановка | + | == Постановка задачі == |
| − | : | + | :Вирішується завдання відновлення регресії. Заданий простір об'єктів <math>x</math> і безліч можливих відповідей <math>y=r</math>. Існує невідома цільова залежність <math> y^*: X \rightarrow Y</math>, значення якої відомі лише на об'єктах навчальної вибірки <math> X^m={(x_i, y_i)}_{i=1}^m</math>. Потрібно побудувати алгоритм <math>a: X \rightarrow Y </math>, що апроксимує цільову залежність <math>y^*</math>. |
| − | |||
| − | |||
| − | |||
== Принцип == | == Принцип == | ||
| − | Принцип, | + | Принцип, використання ідейно простого підхіду до уявлення послідовності вагів <math>\{ W_{mi}(x)\}_{i=1}^m</math> полягає в описі форми вагової функції <math>w_{mi}(x) </math> за допомогою функції щільності із скалярним параметром, який регулює розмір і форму вагів біля х. Цю функцію форми прийнято називати ''''ядром'''' <math>k</math>. |
| − | + | Отримані таким чином ваги далі використовуються для представлення величини <math>a(x) </math> у вигляді зваженої суми значень <math>y_i</math> навчаючої вибірки. | |
| − | |||
| − | + | == Опис методу == | |
| + | === Визначення ядра === | ||
| + | '''Ядро''' — це неперермвна обмеженна симетрична речовина функція <math>K</math> з одиничним інтегралом | ||
| + | ::<math>\int K(u)du=1</math> | ||
| − | == | + | === Послідовність ваги === |
| − | + | Послідовність ваги для ядерних оцінок (для одновимірного <math>x</math>) знаходиться як ::<math>W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}</math>, | |
| − | + | де | |
| − | + | ::<math>\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)</math>, | |
| − | |||
| − | |||
| − | |||
| − | ::< | ||
a | a | ||
| − | ::< | + | ::<math>K_{h_m}(u)=\frac{1}{h_m} K\frac{u}{h_m}</math> |
| − | + | уявимо собі ядро з параметром <math>h_m</math>. Також цей параметр прийнято називати шириной вікна. Підкреслемо залежність <math>h\ =\ h_m</math> від об'єму вибірки <math>m</math>, умова скороченого значення послідовністі ваги <math>W_{mi}(x)</math>. | |
| − | === | + | === Функція ядра === |
| − | + | Функція <math>\hat{f}_{h_m}(x)</math> являєтся ''ядерною оцінкою щільності Розенблата — Парзена'' (Rosenblatt, 1956; Parzen, 1962) для (маргинальної) щільності зміної <math>x</math>. Даний вид ядерних вагів <math>W_{mi}(x)</math> був запропонований в работах (Nadaraya, 1964) і (Watson, 1964). Як наслідок, оцінка очікуваної величини відновлюваної залежності <math>e(y\|x) </math>: ::<math>\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i) Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i)}</math> | |
| − | + | часто називають оцінкою ''Надарая—Ватсона''. | |
| − | + | Ширіна вікна визначає, наскільки швидко убувають ваги <math>w_{mi}(x) </math> у міру видалення об'єктів <math>x_i</math> від <math>x</math>. | |
| − | ::< | ||
| − | часто | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | Характер убування визначається виглядом ядра <math>k</math>. |
| + | Нормалізація вагів <math>\hat{f}_{h_m}(x)</math> гарантує, що сума вагів дорівнює одиниці. | ||
| + | |||
| + | '''Примітка'''. При ряду умов має місце збіжність по вірогідності даної оцінки до <math>e(y|x) </math>. | ||
| − | === | + | === Приклад функції ядра === |
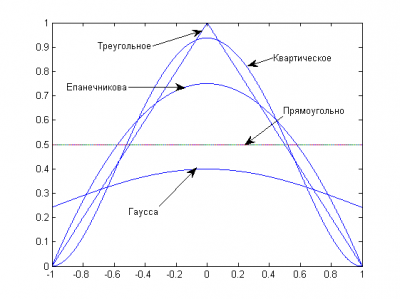
| − | [[ | + | [[Файл:CoreFunc.png|thumb|right|400px|Приклади різних функцій ядра.]] |
| − | На | + | На практиці використовується декілька видів ядерних функцій. |
Чаще всего используется квартическая ядерная функция | Чаще всего используется квартическая ядерная функция | ||
| − | ::< | + | ::<math>K(u)=(15/16)(1-u^2)^2I(\| u \| \le 1)</math>. |
| − | + | Також викоритовуєтьсятся ядро Епанечникова, яке володіє деякими властивостями оптимальності [Хардле В п 4.5]; це функція | |
параболического типа (Epanechnikov, 1969; Bartlett, 1963): | параболического типа (Epanechnikov, 1969; Bartlett, 1963): | ||
| − | ::< | + | ::<math>K(u)=0.75(1-u^2)I(\| u \| \le 1)</math>. |
| − | + | Іншим прикладом є ядро Гаусса, | |
| − | ::< | + | ::<math>K(u)=(2\pi)^{-1/2} \exp(-u^2/2)</math>, |
| − | + | трикутне ядро | |
| − | ::< | + | ::<math>K(u)=(1-\|u\|)I(\| u \| \le 1)</math>, |
| − | + | і прямокутне ядро | |
| − | ::< | + | ::<math>K(u)=(1/2)I(\| u \| \le 1)</math>. |
| − | ''' | + | '''Примітка'''. Точність відновленоії залежності мало залежить від вибору ядра. |
| − | Ядро | + | Ядро визначає міру гладкості функції <math>a(x)</math>. |
| − | === | + | === Залежність від ширини вікна === |
| − | + | Вибір вікна вирішальним чином впливає на точність відновлюваної залежності. При занадто малих значеннях <math>h</math> крива <math>a(x) </math> прагне пройти через кожну точку вибірки, гостро реагуючи на шуми і зазнаючи різкі скачки, оскільки в цьому випадку оцінка опирається лише на невелике число спостережень з вузької окружності точки <math>x</math>. Навпаки, якщо ширина вікна велика, функція надмірно згладжується і в межі при <math> h \rightarrow \infty</math> вироджується в константу -- усереднене значення величин <math> y_i</math>. В цьому випадку згладжена функція не дає можливості визначити характерні особливості шуканої залежності <math> y^*(x) </math>. | |
| − | При | ||
| − | скачки, | ||
| − | |||
| − | |||
| − | == | + | ==Література== |
| − | # | + | # ''Хардле В.''[http://optimization.nlprog.ru/read/ru/8776859F6322A5AF21D45220A9B5B57E110C2E84/index.htm/ Прикладна непараметрична регресія]-1989р. |
| − | + | # ''Воронцов К.В.''[http://www.ccas.ru/voron/download/Regression.pdf/ Лекції по алгоритмам відновлення регресії] - 2007. | |
| − | + | # ''Лагутин М.Б.''Прикладна математична статистика.- 2009 | |
| − | + | ||
| − | + | ==Див. також== | |
| − | |||
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
* [[Алгоритм LOWESS]] | * [[Алгоритм LOWESS]] | ||
| − | * [[ | + | * [[Варіація і зміщення]] |
| − | * [[ | + | * [[Регресійний аналіз]] |
| − | |||
| − | |||
| − | + | ==посилання== | |
| + | [[Непараметрична регресія]] | ||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 20:31, 13 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| {{{img}}} | ||
| Імя | Володимир | |
| Прізвище | Шостак | |
| По-батькові | Михайлович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-11-222 | |
Ядерне згладжуваня - один із найпростіших видів непараметричної регресії.
Зміст
[сховати]Постановка задачі
- Вирішується завдання відновлення регресії. Заданий простір об'єктів x і безліч можливих відповідей y=r. Існує невідома цільова залежність y^*: X \rightarrow Y, значення якої відомі лише на об'єктах навчальної вибірки X^m={(x_i, y_i)}_{i=1}^m. Потрібно побудувати алгоритм a: X \rightarrow Y, що апроксимує цільову залежність y^*.
Принцип
Принцип, використання ідейно простого підхіду до уявлення послідовності вагів \{ W_{mi}(x)\}_{i=1}^m полягає в описі форми вагової функції w_{mi}(x) за допомогою функції щільності із скалярним параметром, який регулює розмір і форму вагів біля х. Цю функцію форми прийнято називати 'ядром' k. Отримані таким чином ваги далі використовуються для представлення величини a(x) у вигляді зваженої суми значень y_i навчаючої вибірки.
Опис методу
Визначення ядра
Ядро — це неперермвна обмеженна симетрична речовина функція K з одиничним інтегралом
- \int K(u)du=1
Послідовність ваги
Послідовність ваги для ядерних оцінок (для одновимірного x) знаходиться як ::W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}, де
- \hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i),
a
- K_{h_m}(u)=\frac{1}{h_m} K\(\frac{u}{h_m}\)
уявимо собі ядро з параметром h_m. Також цей параметр прийнято називати шириной вікна. Підкреслемо залежність h\ =\ h_m від об'єму вибірки m, умова скороченого значення послідовністі ваги W_{mi}(x).
Функція ядра
Функція \hat{f}_{h_m}(x) являєтся ядерною оцінкою щільності Розенблата — Парзена (Rosenblatt, 1956; Parzen, 1962) для (маргинальної) щільності зміної x. Даний вид ядерних вагів W_{mi}(x) був запропонований в работах (Nadaraya, 1964) і (Watson, 1964). Як наслідок, оцінка очікуваної величини відновлюваної залежності e(y\|x): ::\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i) Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i)} часто називають оцінкою Надарая—Ватсона. Ширіна вікна визначає, наскільки швидко убувають ваги w_{mi}(x) у міру видалення об'єктів x_i від x.
Характер убування визначається виглядом ядра k. Нормалізація вагів \hat{f}_{h_m}(x) гарантує, що сума вагів дорівнює одиниці.
Примітка. При ряду умов має місце збіжність по вірогідності даної оцінки до e(y|x).
Приклад функції ядра
На практиці використовується декілька видів ядерних функцій. Чаще всего используется квартическая ядерная функция
- K(u)=(15/16)(1-u^2)^2I(\| u \| \le 1).
Також викоритовуєтьсятся ядро Епанечникова, яке володіє деякими властивостями оптимальності [Хардле В п 4.5]; це функція параболического типа (Epanechnikov, 1969; Bartlett, 1963):
- K(u)=0.75(1-u^2)I(\| u \| \le 1).
Іншим прикладом є ядро Гаусса,
- K(u)=(2\pi)^{-1/2} \exp(-u^2/2),
трикутне ядро
- K(u)=(1-\|u\|)I(\| u \| \le 1),
і прямокутне ядро
- K(u)=(1/2)I(\| u \| \le 1).
Примітка. Точність відновленоії залежності мало залежить від вибору ядра. Ядро визначає міру гладкості функції a(x).
Залежність від ширини вікна
Вибір вікна вирішальним чином впливає на точність відновлюваної залежності. При занадто малих значеннях h крива a(x) прагне пройти через кожну точку вибірки, гостро реагуючи на шуми і зазнаючи різкі скачки, оскільки в цьому випадку оцінка опирається лише на невелике число спостережень з вузької окружності точки x. Навпаки, якщо ширина вікна велика, функція надмірно згладжується і в межі при h \rightarrow \infty вироджується в константу -- усереднене значення величин y_i. В цьому випадку згладжена функція не дає можливості визначити характерні особливості шуканої залежності y^*(x).
Література
- Хардле В.Прикладна непараметрична регресія-1989р.
- Воронцов К.В.Лекції по алгоритмам відновлення регресії - 2007.
- Лагутин М.Б.Прикладна математична статистика.- 2009