Відмінності між версіями «Метод крутого сходження»
| Рядок 1: | Рядок 1: | ||
{{Завдання|Храплива У.В.|Назаревич О. Б.|20 березня 2012}} | {{Завдання|Храплива У.В.|Назаревич О. Б.|20 березня 2012}} | ||
{|border=2 style="float: right; margin-left: 1em; margin-bottom: 0.5em; width: 242px; border: #99B3FF solid 1px" | {|border=2 style="float: right; margin-left: 1em; margin-bottom: 0.5em; width: 242px; border: #99B3FF solid 1px" | ||
| − | |||
|- | |- | ||
| '''Прізвище''' || Храплива | | '''Прізвище''' || Храплива | ||
| Рядок 15: | Рядок 14: | ||
| '''Залікова книжка''' || СНм-11-253 | | '''Залікова книжка''' || СНм-11-253 | ||
|- | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
== Метод крутого сходження (метод Бокса - Уїлсона) == | == Метод крутого сходження (метод Бокса - Уїлсона) == | ||
| − | Метод крутого сходження, або метод Бокса - Уїлсона, поєднує істотні елементи методу Гаусса - Зейделя і градієнтного методу з методами ПФЕ або ДФЕ. Так, при використанні алгоритму крутого сходження кроковий рух з точки здійснюється в напрямі найшвидшого зростання рівня виходу, тобто по, проте, на відміну від градієнтного методу, коректування напряму здійснюється не після кожного наступного кроку, а після досягнення в деякій точці на даному напрямі часткового екстремуму цільової функції (рис. 1), аналогічно методу Гаусса - Зейделя. | + | Метод крутого сходження, або метод Бокса - Уїлсона, поєднує істотні елементи методу Гаусса - Зейделя і градієнтного методу з методами ПФЕ або ДФЕ. Так, при використанні алгоритму крутого сходження кроковий рух з точки <math>(\vec x)_k\</math> здійснюється в напрямі найшвидшого зростання рівня виходу, тобто по <math>\ grad(y({\vec x}_k))</math>, проте, на відміну від градієнтного методу, коректування напряму здійснюється не після кожного наступного кроку, а після досягнення в<br> |
| − | Важливою особливістю методу Бокса - Уїлсона є також регулярне проведення статичного аналізу проміжних результатів на шляху до оптимуму. | + | <center>[[Файл:Рис 1.GIF]]</center><br> |
| − | Порядок виконання операцій при пошуку екстремуму за методом крутого сходження такий: | + | <center>Рисунок 1</center><br> |
| − | 1) проводиться повний або дробовий факторний експеримент з центором у вихідній точці для визначення. Результати експерименту піддаються статистичному аналізу, який включає: | + | |
| − | а) перевірку відтворюваності експерименту; | + | деякій точці <math>{\vec x}_m</math> на даному напрямі часткового екстремуму цільової функції (рис. 1), аналогічно методу Гаусса - Зейделя.<br> |
| − | б) перевірку значщості оцінок коефіцієнтів лінійної моделі об'єкта; | + | Важливою особливістю методу Бокса - Уїлсона є також регулярне проведення статичного аналізу проміжних результатів на шляху до оптимуму. <br> |
| + | Порядок виконання операцій при пошуку екстремуму за методом крутого сходження такий:<br> | ||
| + | 1) проводиться повний або дробовий факторний експеримент з центором у вихідній точці <math>{\vec x}_0</math> для визначення <math>\ grad(y({\vec x}_0))</math>. Результати експерименту піддаються статистичному аналізу, який включає:<br> | ||
| + | а) перевірку відтворюваності експерименту;<br> | ||
| + | б) перевірку значщості оцінок коефіцієнтів <math>b_i</math> лінійної моделі об'єкта;<br> | ||
| + | в) перевірк адекватності утвореної лінійної моделі<br> | ||
| + | <center><math>\ y = {b_0} + {b_1}{x_1} + ... + {b_n}{x_n}</math></center><br> | ||
| + | досліджуваному об'єкту.<br> | ||
| + | Порядок виконання цих операцій детально викладено у попередніх главах;<br> | ||
| + | 2) обчислюються добутки <math>\ b_i \Delta {x_i}</math>, де <math>\Delta {x_i}</math> - крок варіювання параметра <math>x_i</math> при проведенні ПФЕ, і фактор, для якого цей добуток максимальний, береться як базовий<br> | ||
| + | <center><math>\ max (b_i \Delta {x_i}) = {b_\sigma }\Delta {x_\sigma }</math>,</center><br> | ||
| + | 3) для базового фактора вибирають крок варіювання при крутому сходженні <math>\rho</math>, залишаючи старий крок або впроваджуючи дрібніший;<br> | ||
| + | 4) визначаються розміри <math>\rho_j</math> за рештою змінних процесу <math>\ x_j(j \ne i)</math>. Оскільки під час руху по градієнту варійовані параметри повинні змінюватися пропорційно коефіцієнтам <math>\ b_j = {\textstyle{{\Delta y} \over {\Delta {x_j}}}}</math>, які є компонентами вектора <math>\ grad(y(x))</math>, то відповідні <math>\rho_j</math> знаходяться за формулою <br> | ||
| + | <center><math>\rho _j = {\textstyle{{{b_j}\Delta {x_j}} \over {\left| {{b_\sigma }\Delta {x_\sigma }} \right|}}}\rho </math>,</center><br> | ||
| + | де <math>\rho</math> і <math>\Delta {x_j}</math> завжди додатні, а коефіцієнт <math>b_j</math> береться зі своїм знаком;<br> | ||
| + | 5) проводяться уявні досліди, які полягають у завбаченні значень виходу <math> y_k({\vec x}_k)</math> у певних точках <math>{\vec x}_k</math> факторного простору (див. рис.1). Для цього незалежні змінні лінійної моделі обєкта змінюються з урахуванням <math>b_i = \Delta y/\Delta {x_i}</math> таким чином, щоб зображуюча точка <math>\vec x</math> виконувала кроковий рух у напрямі вектора <math>\ grad({\vec x}_1)</math>, займаючи послідовно положення <br> | ||
| + | <center><math>{\vec x}_1,{\vec x}_2,...,{\vec x}_k,...,{\vec x}_m.</math></center><br> | ||
| + | Очевидно, що j-а координата k-ї точки визначається так:<br> | ||
| + | <center><math>x_{kj} = {x_{1j}} + {k_{\rho j}},j = 1,2,...,n.</math></center><br> | ||
| + | Тоді<br> | ||
| + | <center><math>y_k = b_0^' + k\sum\limits_{j = 1}^n {{b_j}{\rho _j}} ,k = 1,2,...,m.</math></center><br> | ||
| + | Зробимо підстановку<br> | ||
| + | <center><math>y_k = k{y_1} - (k - 1){b_0},k = 1,2,...,m,</math></center><br> | ||
| + | або ще зручніше<br> | ||
| + | <center><math>y_k = {y_{k - 1}} + ({y_1} - {b_0}),k = 1,2,...,m.</math></center><br> | ||
| + | 6) уявні досліди продовжуються до тих пір, поки виконується нерівність<br> | ||
| + | <center><math>y_k \le (1...2){y_{\max }}</math>,</center><br> | ||
| + | де <math>y_{max}</math> - максимально можливий вихід, який визначається з фізичних міркувань;<br> | ||
| + | 7) деякі з уявних дослідів (звичайно через кожні 2-3 уявних кроки) реалізуються на обєкті для перевірки відповідності апроксимації обєкта утвореним рівнянням(гіперплощиною). Спостережені значення <math>y_{exper}</math> порівнюють із завбаченими <math>y_{zav}</math> (див. рис.1);<br> | ||
| + | 8) точка <math>{\vec x}_m</math>, де в реальному досліді утворено максимальне значення виходу, береться за нову початкову точку, і етап крутого сходження, описаний вище, повторюється;<br> | ||
| + | 9) оскільки кожен етап крутого сходження наближає зображуючу точку до області екстремуму <math>y(\vec x)</math>, де крутість поверхні відклику менша, то для кожного наступного етапу <math>\rho</math> береться рівним або меншим попереднього;<br> | ||
| + | 10) пошук припиняється,коли всі коефіцієнти <math>b_i, (i=1,2,...,n)</math> лінійної моделі обєкта виходять незначущими. Це свідчить про вихід в область екстремуму цільової функції. | ||
Версія за 14:17, 6 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| Прізвище | Храплива |
| Ім'я | Уляна |
| По батькові | Вікторівна |
| Факультет | ФІС |
| Група | СНм-51 |
| Залікова книжка | СНм-11-253 |
Метод крутого сходження (метод Бокса - Уїлсона)
Метод крутого сходження, або метод Бокса - Уїлсона, поєднує істотні елементи методу Гаусса - Зейделя і градієнтного методу з методами ПФЕ або ДФЕ. Так, при використанні алгоритму крутого сходження кроковий рух з точки [math](\vec x)_k\[/math] здійснюється в напрямі найшвидшого зростання рівня виходу, тобто по [math]\ grad(y({\vec x}_k))[/math], проте, на відміну від градієнтного методу, коректування напряму здійснюється не після кожного наступного кроку, а після досягнення в
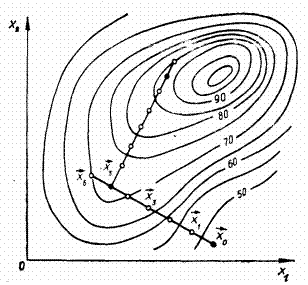
деякій точці [math]{\vec x}_m[/math] на даному напрямі часткового екстремуму цільової функції (рис. 1), аналогічно методу Гаусса - Зейделя.
Важливою особливістю методу Бокса - Уїлсона є також регулярне проведення статичного аналізу проміжних результатів на шляху до оптимуму.
Порядок виконання операцій при пошуку екстремуму за методом крутого сходження такий:
1) проводиться повний або дробовий факторний експеримент з центором у вихідній точці [math]{\vec x}_0[/math] для визначення [math]\ grad(y({\vec x}_0))[/math]. Результати експерименту піддаються статистичному аналізу, який включає:
а) перевірку відтворюваності експерименту;
б) перевірку значщості оцінок коефіцієнтів [math]b_i[/math] лінійної моделі об'єкта;
в) перевірк адекватності утвореної лінійної моделі
досліджуваному об'єкту.
Порядок виконання цих операцій детально викладено у попередніх главах;
2) обчислюються добутки [math]\ b_i \Delta {x_i}[/math], де [math]\Delta {x_i}[/math] - крок варіювання параметра [math]x_i[/math] при проведенні ПФЕ, і фактор, для якого цей добуток максимальний, береться як базовий
3) для базового фактора вибирають крок варіювання при крутому сходженні [math]\rho[/math], залишаючи старий крок або впроваджуючи дрібніший;
4) визначаються розміри [math]\rho_j[/math] за рештою змінних процесу [math]\ x_j(j \ne i)[/math]. Оскільки під час руху по градієнту варійовані параметри повинні змінюватися пропорційно коефіцієнтам [math]\ b_j = {\textstyle{{\Delta y} \over {\Delta {x_j}}}}[/math], які є компонентами вектора [math]\ grad(y(x))[/math], то відповідні [math]\rho_j[/math] знаходяться за формулою
де [math]\rho[/math] і [math]\Delta {x_j}[/math] завжди додатні, а коефіцієнт [math]b_j[/math] береться зі своїм знаком;
5) проводяться уявні досліди, які полягають у завбаченні значень виходу [math]y_k({\vec x}_k)[/math] у певних точках [math]{\vec x}_k[/math] факторного простору (див. рис.1). Для цього незалежні змінні лінійної моделі обєкта змінюються з урахуванням [math]b_i = \Delta y/\Delta {x_i}[/math] таким чином, щоб зображуюча точка [math]\vec x[/math] виконувала кроковий рух у напрямі вектора [math]\ grad({\vec x}_1)[/math], займаючи послідовно положення
Очевидно, що j-а координата k-ї точки визначається так:
Тоді
Зробимо підстановку
або ще зручніше
6) уявні досліди продовжуються до тих пір, поки виконується нерівність
де [math]y_{max}[/math] - максимально можливий вихід, який визначається з фізичних міркувань;
7) деякі з уявних дослідів (звичайно через кожні 2-3 уявних кроки) реалізуються на обєкті для перевірки відповідності апроксимації обєкта утвореним рівнянням(гіперплощиною). Спостережені значення [math]y_{exper}[/math] порівнюють із завбаченими [math]y_{zav}[/math] (див. рис.1);
8) точка [math]{\vec x}_m[/math], де в реальному досліді утворено максимальне значення виходу, береться за нову початкову точку, і етап крутого сходження, описаний вище, повторюється;
9) оскільки кожен етап крутого сходження наближає зображуючу точку до області екстремуму [math]y(\vec x)[/math], де крутість поверхні відклику менша, то для кожного наступного етапу [math]\rho[/math] береться рівним або меншим попереднього;
10) пошук припиняється,коли всі коефіцієнти [math]b_i, (i=1,2,...,n)[/math] лінійної моделі обєкта виходять незначущими. Це свідчить про вихід в область екстремуму цільової функції.