Температурні залежності в'язкості рідин
Температурна залежність в’язкості рідини - явище, при якому в'язкість рідини має тенденцію до зменшення (або, як альтернатива, його плинність має тенденцію до збільшення), як тільки його температура зростає.
Це можна спостерігати, наприклад, шляхом спостереження за тим, як рослинна олія, рухається більш плавно по сковорідці після нагрівання.
Фізичні причини
Головною причиною в'язкості рідини є сили взаємного притягання її молекул. Так, як при нагріванні речовини розширюються, то і сили взаємного притягання їх молекул при цьому зменшуються, чим і пояснюється зменшення в'язкості речовин при збільшені температури.
Емпіричні рівняння залежності в'язкості від температури
Запропоновано значне число емпіричних формул, що пов'язують в'язкість рідин з їх температурою. Найбільш прості з них представляють собою звичайні інтерполяційні формули або їх варіанти, прийняті при підборі емпіричних формул. До їх числа відносяться формула Пуазейля:
[math]\mu_t\ = \frac{ \mu_0\ }{1 + \alpha\ t + \beta\ t^2} \qquad(1)[/math]
і формула Торпа і Роджерса:
[math]\mu_t\ = \frac{C}{1 + \alpha\ t + \beta\ t^2 } \qquad(2)[/math]
Постійні величини, що входять в ці формули (С, α, β), не мають фізичного сенсу. Близькі до таких формул рівняння температурної залежності плинності, запропоновані Бінгамом:
[math]\varphi_t\ = A t \qquad(3)[/math]
де А - постійна.
Однак ця формула має досить обмежене застосування. Більш широко застосовується основна формула Бінгама з трьома константами, але для води, спиртів та інших рідин, що містять гідроксильну групу, формула непридатна.
Кращі результати дає емпіричне рівняння Бінгама з чотирма постійними:
[math]\varphi_t\ = A_\varphi\ + \frac{B}{ \varphi\ + \alpha\ } + C \qquad(4)[/math]
Рівняння цього типу будуть передавати в'язкісно-температурну залежність тим точніше, чим більше в них постійних величин. Однак зростання числа постійних ускладнює їх застосування, так як кількість експериментальних вимірювань, які потрібно виробляти для обчислення постійних, не є меншими від їх числа. Для застосування формул (1, 2, 3) необхідно вимірювати в'язкість принаймні при трьох температурах.
Емпіричні формули з двома постійними зазвичай передають з достатнім наближенням залежність в'язкості від температури простих нормальних рідин.
Для багатьох нормальних рідин, а також для деяких не дуже вузьких аномальних рідин, можуть бути застосовні емпіричні співвідношення типу формули Слотта:
[math]\mu_t\ = \frac{A}{(t \pm B)^n} \qquad(5)[/math]
яка була перевірена на 70 рідинах (переважно нормальних), досліджених Торпом і Роджером.
[math]\lg \mu_t\ = K_1 - K_2 \lg t \qquad(6)[/math]
Значний інтерес представляє група емпіричних рівнянь, розроблена для вираження в'язкісно-температурної залежності нафтопродуктів, розплавленого скла і аналогічних за своїми механічними властивостями аномальних рідин
Порівняно давно І. Д. Афанасьєв на великому експериментальному матеріалі показав, що багато масел в координатах дають прямі або криві, близькі до прямих. Степенева або експоненціальна залежність в'язкості від температури лежить в основі всіх емпіричних формул розглянутого типу. Для розплавленого скла, у яких в'язкість дуже сильно залежить від температури, Ле-Шательє запропонував формулу:
[math]\mu_t\ = e^\frac{C}{T^ \alpha\ } \qquad(7)[/math]
де е - основа натурального логарифма; Т - абсолютна температура; а і С константи. У логарифмічною формі рівняння (7) має вигляд:
[math]\lg \lg \mu_t\ = A - Bt \qquad(8)[/math]
П.П. Лазарєв, а також Б.В. Дерягин і І.Я. Хананом довели, що більш хороші результати можна отримати, якщо ввести в цю формулу ще одну постійну:
[math]\lg \lg \frac{ \mu_t\ }{ \mu_a\ } = A - Bt \qquad(8)[/math]
[math]\mu_0\[/math] можна обчислити із співвідношення:
[math]\mu_0\ = \frac{ \lg \mu_1\ \lg \mu_2\ - \lg \mu_2\ }{ \lg \mu_1\ + \lg \mu_2\ - 2\lg \mu_2\ } \qquad(9)[/math]
Широке росповсюдження в змащувальній справі отримало рівняння Вальтера, яке також є варіантом рівняння Ле-Шательє. В експоненційної формі воно має вигляд:
[math]( \nu_t\ + 0.8) = e^{ \frac{C}{T^ \alpha\ } } \qquad(10)[/math]
[math]( 100\nu_t\ + 0.8)^{T^c} = k \qquad(11)[/math]
де [math]\nu\[/math] виражено в сСт.
Двічі логарифмуючи це рівняння, отримаємо:
[math]C \lg T + \lg \lg (100 \nu_t\ + 0.8) = \lg \lg k \qquad(12)[/math]
вводячи позначення [math]\lg \lg k = A\ i\ C = B[/math], отримуємо звичайну логарифмічну форму рівняння Вальтера:
[math]\lg \lg (100 \nu_t\ + 0.8) = A - B \lg T \qquad(13)[/math]
Широке застосування рівняння Вальтера пов'язано з тим, що на його основі побудовані прості номограми для обчислення в'язкості масел та інших нафтопродуктів при різних температурах.
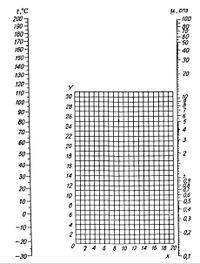
Графічна інтерполяція і екстраполяція значення в’язкості рідини
Для графічної інтерполяції і екстраполяції значень в’язкості рідин може служити номограма Перрі, приведена на рисунку. Координати точок, відповідають різним рідинам, приведених в таблиці . Проводячи через точку на сітці і точку на лівій осі, відповідну температурі, яка нас цікавить, пряму до перетину з правою віссю, вираховують в точці перетину шукане значення в’язкості. Для рідин не приведених в таблиці, координати можна визначити якщо відоме значення в’язкості цієї ж рідини при двох різних значеннях температури. В цьому випадку прямою з'єднують значення в’язкості на правій осі і відповідні їм температури на лівій осі. Точка перетину цих прямих на сітці номограми і є шукана точка; її координати відраховують на осях сітки. Для кожної рідини, положення точки якої на сітці відоме, по рисунку можна визначити в’язкість при любій температурі.