Відмінності між версіями «Непараметрична регресія»

(→‎Оценки ортогональных разложений)
 
(Не показані 87 проміжних версій 3 користувачів)
Рядок 1: Рядок 1:
−
{{Завдання|Шостак В.М.|Назаревич О. Б.|10 березня 2012}}
 
 
{{Студент | Name=Володимир | Surname=Шостак | FatherNAme=Михайлович |Faculti=ФІС | Group=СН-51 | Zalbook=СН-11-222}}
 
{{Студент | Name=Володимир | Surname=Шостак | FatherNAme=Михайлович |Faculti=ФІС | Group=СН-51 | Zalbook=СН-11-222}}
−
'''Непараметрическая регрессия''', в отличие от параметрических подходов, использует модель, которая не описывается конечным числом параметров.
+
'''Непараметрична регресія''', на відміну від параметричних підходів, використовує модель, яка не описується кінцевим числом параметрів.
  
−
== Введение ==
+
:Мета ''регресійного аналізу'' полягає у наступному, здійсненні розумної апроксимації невідомої функції відгуку <math>Y(X)</math> по відомим точкам <math>(X_i,Y_i)_{i = 1}^{m}</math>. У випадку малих помилок спостереження стає можливим сконцентрувати увагу на важливих деталях середньої залежності <math>Y</math> від <math>X</math> при її інтерпретації.
−
:Цель регрессионного анализа состоит в осуществлении разумной аппроксимации неизвестной функции отклика <math>Y(X)</math> по известным точкам <math>(X_i,Y_i)_{i=1}^{m}</math>. В случае малых ошибок наблюдения становится возможным сконцентрировать внимание на важных деталях средней зависимости <math>Y</math> от <math>X</math> при ее интерпретации.
 
  
−
== Отличие от параметрических подходов ==
+
== Відмінність від параметричних підходів ==
−
:Процедура аппроксимации обычно называется '''''сглаживанием'''''. По существу эта аппроксимация функции отклика <math>Y</math> может быть выполнена двумя способами. Довольно часто используется параметрический подход, заключающийся в предположении, что функция отклика <math>Y</math> имеет некоторую предписанную функциональную форму, например, это прямая линия с неизвестными свободным членом и наклоном. Альтернативой этому может служить попытка оценить <math>Y</math> непараметрическим образом, без указания конкретного ее вида. Первый подход к анализу регрессионной зависимости называется параметрическим, поскольку предполагается, что вид функции полностью описывается конечным набором параметров. Типичный пример параметрической модели представляет собой полиномиальное уравнение регрессии, когда параметрами являются коэффициенты при неизвестных. Однако при параметрическом подходе молчаливо предполагается, что кривая может быть представлена в терминах параметрической модели, или, по крайней мере, имеется уверенность в том, что ошибка аппроксимации для наилучшего параметрического приближения пренебрежимо мала. Наоборот, в непараметрической модели регрессионной зависимости не производится проектирования данных в "прокрустово ложе" фиксированной параметризации. Предварительное задание параметрической модели может оказаться слишком ограничительным или чересчур малой размерности для аппроксимации непредвиденных характеристик, в то время как непараметрическое сглаживание предоставляет гибкие средства анализа неизвестных регрессионных зависимостей.
+
:Процедура апроксимації зазвичай називається '''''згладжуванням'''''. По суті ця апроксимація функції відгуку <math>Y</math> може бути виконана двома способами. Досить часто використовується параметричний підхід, що полягає у припущенні, що функція відгуку <math>Y</math> має деяку визначену функціональну форму, наприклад, це пряма лінія з невідомим вільним членом і нахилом. Альтернативою цьому може служити спроба оцінити <math>Y</math> непараметричним чином, без вказівки конкретного її виду. Перший підхід до аналізу регресійної залежності називається параметричним, оскільки передбачається, що вид функції повністю описується кінцевим набором параметрів. Типовий приклад параметричної моделі є поліноміальне рівняння регресії, коли параметрами є коефіцієнти при невідомих. Однак при параметричному підході передбачається, що крива може бути представлена в термінах параметричної моделі, або, принаймні, є впевненість в тому, що помилка апроксимації для найкращого параметричного наближення є дуже малою. Навпаки, в непараметричної моделі регресійної залежності не проводиться проектування даних в "прокрустове ложе" фіксованої параметризації. Попереднє завдання параметричної моделі може виявитися занадто обмежувальним, або надто малої розмірності для апроксимації непередбачених характеристик, в той час, як непараметричне згладжування надає гнучкості засобам аналізу невідомих регресійних залежностей.
  
−
:Непараметрический подход приводит, таким образом, к гибкому функциональному виду кривой регрессии.
+
:Непараметричний підхід приводить, таким чином, до гнучкого функціонального виду кривої регресії.
  
−
== Разновидности ==
+
== Різновиди ==
−
== Ядерное сглаживание==
 
−
:Одним из простейших методов является [[ядерное сглаживание]]. Этот метод прост в применении, не требует дополнительных математических сведений и понятен на интуитивном уровне. Ядерное сглаживание во многих случаях является подходящим средством. Существуют разнообразные альтернативные методы сглаживания такие, например, как сплайны, но в [Хардле В, гл3] показывается, что в асимптотическом смысле они эквивалентны [[ядерное сглаживание|ядерному сглаживанию]].
 
  
−
:Ключом к проведению '''качественного непараметрического оценивания''' является выбор подходящей ширины окна для имеющейся задачи. Хотя ядерная функция <math>K</math> остается важной, ее главная роль состоит в обеспечении дифференцируемости и гладкости получающейся оценки. Ширина  окна <math>h</math>, с  другой  стороны, определяет  поведение  оценки  в  конечных  выборках, что  ядерная  функция  сделать  просто  не  в состоянии. Существуют  четыре  общих  подхода к выбору ширины окна:
+
== Ядерне згладжування==
−
#референтные эвристические правила
+
:Одним із найпростіших методів є [[ядерне згладжування]]. Цей метод простий у застосуванні, не вимагає додаткових математичних відомостей і зрозумілий на інтуїтивному рівні. Ядерне згладжування в багатьох випадках є підходящим засобом. Існують різноманітні альтернативні методи згладжування такі, наприклад, як сплайни, але в [Хардле В., Заг 3] показується, що в асимптотичному сенсі вони еквівалентні [[ядерне згладжування | ядерному згладжуванню]].
−
#методы подстановки
 
−
#методы  кросс-валидации
 
−
#бутстраповские  методы. 
 
−
Ради  аккуратности  подчеркнем, что диктуемые данными методы выбора ширины окна <tex>h</tex> не всегда гарантируют хороший результат.  
 
  
−
:Исходя из минимизации глобальной ошибки следует <math>h</math> брать равным::
+
: Ключем до проведення '''якісного непараметричного оцінювання''' є вибір відповідної ширини вікна для наявного завдання. Хоча ядерна функція <math>K</math> залишається важливою, її головна роль полягає в забезпеченні диференцієваності і гладкості отримуваної оцінки. Ширина вікна <math>h</math>, з іншого боку, визначає поведінку оцінки в кінцевих вибірках, що ядерна функція зробити просто не в змозі. Існують чотири загальні підходи до вибору ширини вікна:
−
::<math>h_{opt}=\[ \frac{\int{K^2(z)dz}}{ \(\int{z^2K^2(z)dz} \)^2 \int{\[y''(x)\]^2dx}  }\]^{-1/5} m^{-1/5} </math>, где <math>y(x)</math> - неизвестная аппроксимируемая зависимость.  
+
#референтні евристичні правила;
 +
#методи підстановки;
 +
#методи  крос-валідації;
 +
#бутстаповскі  методи.
  
−
=== Референтные эвристические правила ===
+
Заради об'єктивності підкреслимо, що подані дані методи вибору ширини вікна <math>h</math> не завжди гарантують гарний результат.
−
:Референтные  эвристические правила выбора ширины окна используют стандартное семейство распределений для определения <math>h_{opt}</math>.  
+
:Виходячи з мінімізації глобальної помилки потрібно <math>h</math> брати рівним:
−
Рассмотрим  оценку Парзена-Розенблата для одномерной  функции  плотности
+
::<math>h_{opt}=\[ \frac{\int{K^2(z)dz}}{ \(\int{z^2K^2(z)dz} \)^2 \int{\[y''(x)\]^2dx}  }\]^{-1/5} m^{-1/5} </math>, де <math>y(x)</math> - невідома апроксимируюча залежність.
 +
 
 +
=== Референтні евристичні правила ===
 +
:Референтні евристичні правила вибору ширини вікна використовують стандартне сімейство розподілів для визначення <math>h_{opt}</math>.  
 +
Розглянемо оцінку Парзена-Розенблата для одновимірної функції щільності
 
:: <math>\hat{y}(x)=\frac{1}{mh} \sum_{i=0}^m{K\( \frac{X_i-x}{h}\)}</math>.
 
:: <math>\hat{y}(x)=\frac{1}{mh} \sum_{i=0}^m{K\( \frac{X_i-x}{h}\)}</math>.
−
:В случае семейства нормальных распределений и гауссовского ядра <tex>h_{opt}=1.059*\sigma m^{-1/5}</tex>. На практике применяется <math>\hat{\sigma}</math>, выборочное стандартное отклонение.
+
:У випадку сімейства нормальних розподілів і гаусівського ядра <math>h_{opt}=1.059*\sigma m^{-1/5}</math>. На практиці застосовується <math>\hat{\sigma}</math>, вибіркове стандартне відхилення.
  
−
=== Методы подстановки ===
+
=== Методи підстановки ===
−
Методы подстановки, такие как в Sheather,  Jones  (1991), состоят  в  подстановке  оценок неизвестной константы <math>\int{\[y''(x)\]^2dx</math> в формулу для оптимальной ширины окна на основе первоначальной оценки <math>y''(x)</math>, которая в свою очередь основана на «'''''предварительной'''''» ширине окна, например, найденной по правилу  <math>1.059*\sigma m^{-1/5}</math> . Все прочие константы в выражении для <math>h_{opt}</math>  известны после выбора ядерной функции <math>K</math> (то есть <math>\int{K^2(z)dz}</math>  и <math>\int{z^2K^2(z)dz}</math> известны). Хотя такие правила популярны, заинтересованный читатель может обратиться к работе Loader (1999), где  обсуждаются  относительные  достоинства  методов  подстановки  по  сравнению  с другими методами выбора ширины окна, обсуждаемыми ниже.
+
Методи підстановки, такі як в Sheather,  Jones  (1991), полягають у підстановці оцінок невідомої константи <math>\int{\[y''(x)\]^2dx</math> в формулу для оптимальної ширини вікна на основі первинної оцінки <math>y''(x)</math>, яка в свою чергу заснована на «'''''попередній'''''» ширині вікна, наприклад, знайденої за правилом <math>1.059*\sigma m^{-1/5}</math> . Всі інші константи у виразі для <math>h_{opt}</math>  відомі після вибору ядерної функції <math>K</math> (отже <math>\int{K^2(z)dz}</math>  і <math>\int{z^2K^2(z)dz}</math> відомі). Хоча такі правила популярні, зацікавлений читач може звернутися до праць Loader (1999), де обговорюються відносні переваги методів підстановки в порівнянні з іншими методами вибору ширини вікна, обговорюваними нижче.
  
−
=== Методы кросс-валидации ===
+
=== Методи крос-валідації ===
−
:Методы кросс-валидация на основе наименьших квадратов – это полностью автоматический и диктуемый данными метод выбора сглаживающего параметра. Этот метод основан на принципе выбора  ширины  окна, минимизирующей  интегральную среднеквадратическую  ошибку  получающейся оценки. Интеграл квадрата разности <tex>y(x)</tex> и <tex>\hat{y}(x)</tex> имеет вид
+
:Методи крос-валідації засновані на основі найменших квадратів – це повністю автоматичний і диктуються даними методу вибору згладжуваного параметра. Цей метод заснований на принципі вибору ширини вікна, мінімалізує інтегральну средньоквадратичну помилку отримуваної оцінки. Інтеграл квадрата різниці <math>y(x)</math> и <math>\hat{y}(x)</math> має вигляд
  
 
::<math>\int{\[y(x) - \hat{y}(x)\]^2dx } = \int{y^2(x)dx} - 2*\int{y(x)\hat{y}(x)dx} + \int{\hat{y}^2(x)dx}</math>
 
::<math>\int{\[y(x) - \hat{y}(x)\]^2dx } = \int{y^2(x)dx} - 2*\int{y(x)\hat{y}(x)dx} + \int{\hat{y}^2(x)dx}</math>
  
−
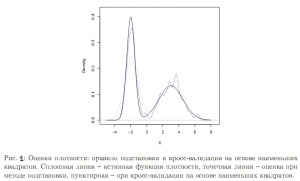
[[Изображение:Example_density.jpg|right|300px]]
+
[[Файл:300px-Example_density.jpg|300px|thumb|right|Рис. 1. Оцінка щільності правила підстановки крос-валідаціїна на основі найменших квадратів]]
−
:Можно заменить эти величины их выборочными аналогами, сделать поправку на смещение и получить целевую функцию, которую затем можно минимизировать с помощью численных методов. Этот подход был предложен в работах Rudemo (1982) и Bowman (1984). Для понимания  сущности  комментариев  в Loader (1999) на '''Рис. 1''' изображены  оценки бимодальной  плотности  –  ядерная  оценка  при применении  правила подстановки  и  кросс-валидации на основе наименьших квадратов. '''Рис. 1''' показывает, что на самом деле правило подстановки  чрезмерно  сглаживает, приводя  к  существенному  смещению  в левой  вершине. Кросс-валидация    на основе  наименьших    квадратов  исправляет    это, как  отмечает    Loader (1999), но ценой дополнительной вариации в правой вершине.  
+
:Можна замінити ці величини їх вибірковими аналогами, зробити поправку на зсув і отримати цільову функцію, яку потім можна мінімізувати за допомогою чисельних методів. Цей підхід був запропонований в роботах Rudemo (1982) і Bowman (1984). Для розуміння сутності коментарів у Loader (1999) на '''Рис. 1''' зображені оцінки бімодальної щільності - ядерна оцінка при застосуванні правила підстановки і крос-валідації на основі найменших квадратів. '''Рис. 1'''показує, що насправді правило підстановки надмірно згладжує, приводячи до істотного зсуву в лівій вершині. Крос-валідація на основі найменших квадратів виправляє це, як зазначає Loader (1999), але ціною додаткової варіації в правій вершині.
−
:Одна из  проблем данного  подхода  –  его  чувствительность  к  наличию  округленных  или дискретизированных данных, а также к мелкомасштабным эффектам в данных.  
+
: Одна з проблем даного підходу - його чутливість до наявності округлених або Дискретизований даних, а також до дрібномасштабних ефектів у даних.
−
:Из примера следует, что, возможно, ядерную оценку с фиксированным параметром <math> h </math> можно улучшить, и существуют «адаптивные» ядерные оценки, которые позволяют <math> h </math> меняться в точке <math>x</math> или <math>X_i</math> ; см. Abramson (1982) и Breiman, Meisel, Purcell (1977). Эти оценки, однако, способствуют введению ложного шума в оценку плотности. Однако метод с фиксированным <math> h </math> доминирует в прикладных исследованиях.
+
:З прикладу випливає, що, можливо, ядерну оцінку з фіксованим параметром <math>h</math> можна поліпшити, і існують «адаптивні» ядерні оцінки, які дозволяють <math>h</math> змінюватися в точці <math>x</math> або <math>X_i</math>; див. Abramson (1982) і Breiman, Meisel, Purcell (1977). Ці оцінки, однак, сприяють введенню помилкового шуму в оцінку щільності. Однак метод з фіксованим <math>h</math> домінує в прикладних дослідженнях.
  
−
=== Бутстраповские методы ===
+
=== Бутстраповскі методи ===
−
:Faraway, Jhun (1990) предложили метод выбора ширины окна <math>h</math> на основе бутстрапа путем оценивания интегральной среднеквадратичной ошибки для каждой  фиксированной  ширины  окна,  и  затем  минимизации по всем значениям. Данный подход использует сглаженный бутстраповский метод на основе начальной оценки плотности. Один из недостатков этого подхода в том, что целевая функция является случайной, что может привести к проблемам при численной минимизации, а также его вычислительная сложность.
+
: Faraway, Jhun (1990) запропонували метод вибору ширини вікна <math>h</math> на основі бутстрапа, шляхом оцінювання інтегральної середньоквадратичної помилки для кожної фіксованої ширини вікна, і потім мінімізації її по всіх значеннях. Даний підхід використовує згладжений бутстраповский метод на основі початкової оцінки щільності. Один з недоліків цього підходу в тому, що цільова функція є випадковою, що може привести до проблем при чисельній мінімізації, а також її обчислювальної складністі.
  
 
----
 
----
  
−
Ядерные веса определяют некоторую окрестность вокруг  точки <math>x</math> лежащей на сетке. Следующий вопрос сглаживания –  полиномиальное приближение функции <math>y</math> в этой окрестности.
+
Ядерні ваги визначають деяку ділянку навколо точки <math>x</math> що лежить на сітці. Наступне питання згладжування - поліноміальні наближення функції <math>y</math> в цій ділянці.
−
==== Локально полиномиальное приближение ====
+
==== Локально поліноміальні наближення ====
−
[[Изображение:Example_polynom.jpg|thumb|right|300px|Рис. 2. Локально полиномиальное сглаживание]]
+
[[Файл:300px-Example_polynom.jpg|300px|thumb|right|Рис. 2. Локально поліноміальні згладжування]]
−
:Простейшим полиномом приближения в такой окрестности является константа. Ядерная оценка минимизирует сумму квадратов невязок в окрестности точки <math>x</math>, форма и размер которой определяется ядром <math>K</math>.  
+
:Найпростішим поліномом наближення в такій околиці є константа. Ядерна оцінка мінімізує суму квадратів неув'язок в околиці точки <math>x</math>, форма і розмір якої визначається ядром <math>K</math>.  
−
:Локально полиномиальное приближение и его связь с ядерным сглаживанием подробно исследованы в работе (Muller 1987), где показана их '''эквивалентность'''.
+
:Локально поліноміальні наближення і їх зв'язок з ядерним згладжуванням детально досліджені в працях (Muller 1987), де показана їх '''еквівалентність'''.
 +
:Детальніше також див. [[Алгоритм LOWESS]]
  
−
:Подробнее также см. [[Алгоритм LOWESS]]
+
== k-NN оцінки==
 +
[[Файл:300px-Example_knn.jpg|300px|thumb|right|Рис. 3. k-NN згладжування]]
 +
:Конструкція оцінок [[Метод найближчих сусідів | найближчих сусідів]] відрізняється від ядерних оцінок. Ядерна оцінка визначається як зважене середнє змінних відгуку у фіксованій ділянці точки <math>x</math>, причому ваги визначалися ядром <math>K</math> і шириною вікна <math>h</math>. Оцінка '''''k-найближчих сусідів''''' є середнім, зваженим в мінливих ділянках. Ця ділянка визначається тільки тими значеннями змінної <math>X</math>, які в <math>k</math> є найближчими до <math>x</math> за евклідом ('''звичайної''') віддалі. Послідовність <math>k-NN</math> ваг була введена в роботі Loftsgaarden, Quesenberry (1965) для близької задачі оцінювання щільності і використовувалася в Cover, Hart (1967) для цілей класифікації.
 +
: Параметр згладжування <math>k</math> визначає ступінь гладкості оцінки кривої. Він грає ту ж роль, що і ширина вікна для ядерних згладжувань. Вплив змінного <math>k</math> на якісні характеристики оцінки '''аналогочно випадку ядерних оцінок з прямокутним ядром'''.
  
−
== kNN оценки==
+
:На '''Рис. 3.''' Зображений приклад порівняння ядерного згладжування з [[ядерне згладжування | квартіческім ядром]] і <math>k-NN</math> згладжування. Ширина вікна вибиралася методом [[крос-перевірки]]. Дані пропускались через вікна шириною <math>h = 0.25</math> для ядерного згладжування на відрізку <math>[0,3]</math> і <math>h = 0.15</math> для осі значень. Отримані криві регресії практично збігаються для <math>x\le 1</math>, де лежить велика частина даних. При більших значеннях <math>x</math> спостерігається істотна розбіжність кривих: ядерна оцінка показує очевидне бімодальне співвідношення, а симетризована оцінка найближчих сусідів вказує або на асимптоту, або навіть на слабке спадання із зростанням доходу. В контексті завдання, здається, що останнє містить більше сенсу з точки зору економіки ...
−
[[Изображение:Example_knn.jpg|thumb|right|300px|Рис. 3. k-NN сглаживание]]
 
−
:Конструкция оценок [[Метод ближайших соседей|ближайших соседей]] отличается от ядерных оценок. Ядерная оценка определяется как взвешенное среднее перемененных отклика в фиксированной окрестности точки <math>x</math>, причем веса определялись ядром <math>K</math> и шириной окна <math>h</math>. Оценка '''''k-ближайших соседей ''''' представляет собой среднее, взвешенное в изменяющейся окрестности. Эта окрестность определяется только теми значениями переменной <math>X</math>, которые являются <math>k</math> ближайшими к <math>x</math> по евклидову ('''обычно''') расстоянию. Последовательность <math>k-NN</math> весов была введена в работе Loftsgaarden, Quesenberry (1965) для близкой задачи оценивания плотности и использовалась в Cover, Hart(1967) для целей классификации.
 
−
:Параметр сглаживания <math>k</math> определяет степень гладкости оценки кривой. Он играет ту же роль, что и ширина окна для ядерных сглаживателей. Влияние переменного <math>k</math> на качественные характеристики оценки '''аналогочино случаю ядерных оценок с прямоугольным ядром'''.
 
  
−
:На '''Рис. 3.''' изображен пример сравнения ядерного сглаживания с [[ядерное сглаживание|квартическим ядром]] и <math>k-NN</math> сглаживания. Ширина окна выбиралась методом [[кросс-проверки]]. Данные прогонялись через окна шириной <math>h=0.25</math> для ядерного сглаживания на отрезке <math>[0,3]</math> и <math>h=0.15</math> для оси значений. Получившиеся кривые регрессии практически совпадают для <math>x\le 1</math>, где лежит большая часть данных. При бо‘льших значения <math>x</math> наблюдается существенное расхождение кривых: ядерная оценка показывает очевидное бимодальное соотношение, а симметризованная оценка ближайших соседей указывает либо на асимптоту, либо даже на слабое убывание с ростом дохода. В контексте задачи, кажется, что последнее содержит больше смысла с точки зрения экономики...
+
== Оцінки ортогональних розкладань ==
−
 
+
[[Файл:300px-Example_fur.jpg|300px|thumb|right|Рис. 4. Згладжування з допомогою ортогональних розкладань]]
−
== Оценки ортогональных разложений ==
+
Припустимо, що функція регресії може бути представлена у вигляді ряду Фур'є
−
[[Файл:Example_fur.jpg|thumb|right|300px|Рис. 4. Сглаживание c помощью ортогональных разложений]]
 
−
Предположим, что функция регрессии может быть представлена в виде ряда Фурье
 
 
::<math>y(x)=\sum_{j=0}^{\infty}\beta_j\varphi_j(x)</math>,  
 
::<math>y(x)=\sum_{j=0}^{\infty}\beta_j\varphi_j(x)</math>,  
−
:где <math>{\{\varphi_j\}}_{j=0}^\infty</math> - известна система базисных функций, а <math>{\{\beta_j\}}_{j=0}^\infty</math> - неизвестные коэффициенты Фурье. В работе Szego (1959) приведены условия, при которых такое представление возможно. Хорошо известными системами базисных функций являются [[полиномы Лагерра]] и [[полиномы Лежандра]]. Как только фиксирован базис функций, проблема оценивания функции регрессии может быть сведена к оцениванию коэффициентов Фурье. Конечно, существует определенная трудность, состоящая в том, что может быть бесконечно много ненулевых коэффициентов <math>\beta_j</math>. Таким образом, при заданном конечном объеме выборки <math>m</math> можно эффективно оценить лишь подмножество коэффициентов.
+
:де <math>{\{\varphi_j\}}_{j=0}^\infty</math> - відома система базисних функцій, а <math>{\{\beta_j\}}_{j=0}^\infty</math> - невідомі коефіцієнти Фур'е. В работі Szego (1959) наведені умови, за яких таке подання можливе. Добре відомими системами базисних функцій є [[поліноми Лагерра]] та [[поліноми Лежандра]]. Як тільки фіксований базис функцій, проблема оцінювання функції регресії може бути зведена до оцінювання коефіцієнтів Фур'є. Звичайно, існує певна складність, яка полягає в тому, що може бути нескінченно багато ненульових коефіцієнтів <math>\beta_j</math>. Таким чином, при заданому кінцевому обсязі вибірки <math>m</math> можна ефективно оцінити лише підмножину коефіцієнтів.
  
−
:Пример применения показан на '''Рис. 4.'''
+
: Приклад застосування показаний на'' 'Рис. 4.'' '
  
−
== Сглаживание сплайнами ==
+
== Згладжування сплайнами ==
−
[[Файл:Example_spline.jpg|thumb|right|300px|Рис. 5. Сглаживание с помощью сплайнов]]
+
[[Файл:300px-Example_spline.jpg|300px|thumb|right|Рис. 5. Згладжування за допомогою сплайнів]]
−
Общей мерой близости к данным для некоторой кривой <math>g</math> является сумма  квадратов невязок
+
Загальною мірою близькості до даних для деякої кривої <math>g</math> є сума квадратів нев'язок
 
::<math>\sum_{i=1}^{n}{(Y_i-g(X_i))}^2</math>
 
::<math>\sum_{i=1}^{n}{(Y_i-g(X_i))}^2</math>
  
−
:Если <math>g</math> может любой кривой - неограниченной в функциональном смысле - то эта мера, имеющая смысл расстояния, равна нулю для всякой кривой <math>g</math>, интерполирующей данные. Подход, основанный на сглаживании сплайнами, исключает эту нежелательную интерполяцию данных за счет достижения компромисса между двумя противоречивыми целями: получить хорошую аппроксимацию данных и получить кривую, не имеющую слишком быстрых локальных изменений.
+
:Якщо <math>g</math> може будь кривою - необмеженої в функціональному сенсі - то цей захід, що має сенс відстані, дорівнює нулю для всякої кривої <math>g</math>, інтерполюється дані. Підхід, заснований на згладжуванні сплайнами, виключає цю небажану інтерполяцію даних за рахунок досягнення компромісу між двома суперечливими цілями: отримати гарну апроксимацію даних і отримати криву, яка не має надто швидких локальних змін.
−
:Известны различные способы количественной оценки локальных изменений. Можно определить меру плавности кривой, основанную, например, на первой, второй, и более старших производных. Для успешного раскрытия основной идеи удобнее всего ввести интеграл от квадрата второй производной, т.е. для количественной оценки локального изменения использовать '''''штраф за нарушение плавности'''''   
+
:Відомі різні способи кількісної оцінки локальних змін. Можна визначити міру плавності кривої, засновану, наприклад, на першій, другій, і більш старших похідних. Для успішного розкриття основної ідеї найзручніше ввести інтеграл від квадрата другої похідної, тобто для кількісної оцінки локального зміни використовувати '''''штраф за порушення плавності'''''   
 
::<math>\int {(g''(x))}^2dx</math>.
 
::<math>\int {(g''(x))}^2dx</math>.
−
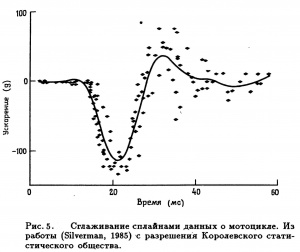
:Пример сглаживания сплайнами представлен на '''Рис. 5.''' интерпретация данных: данные о мотоцикле [ Значения <math>X</math> (в мс) после смоделированного столкновения с мотоциклом. Переменная отклика <math>Y</math> - ускорение (в g) посмертного тестирования объекта. Из Schmidt, Mattern, Schiiler (1981)]
+
:Приклад згладжування сплайнами представлений на '''Рис. 5.'''Інтерпретація даних: дані про мотоциклі [Значення <math>X</math> (в мс) після змодельованого зіткнення з мотоциклом. Мінлива відгуку <math>Y</math> - прискорення (в g) посмертного тестування об'єкта. З Schmidt, Mattern, Schiiler (1981)]
  
−
== Перечень менее распространенных методов ==
+
== Перелік менш поширених методів==
−
[[Файл:Example_regr.jpg|thumb|right|300px|Рис. 6. Регрессограмма]]
+
[[Файл:300px-Example_regr.jpg|thumb|right|300px|Рис. 6. Регрессограмма]]
−
=== Рекуррентные методы ===
+
=== Рекурентні методи ===
−
:Предположим, что данные <math>\{(X_i,Y_i)\}_{i\ge l}</math> наблюдаются не как выборка фиксированного объема <math>m</math>, а как последовательность пар <math>(X_1,Y_1),(X_2,Y_2),\ldots </math> поступающих с выхода некоторого устройства наблюдения. Такие устройства присутствуют в задачах контроля (surveillance problems), управления (control operations) или вмешательства(intervention problems). В общем случае можно рассматривать данные как временной ряд. Поскольку непараметрическая
+
:Припустимо, що дані <math>\{(X_i,Y_i)\}_{i\ ge l}</math> спостерігаються не як вибірка фіксованого обсягу <math>m</math>, а як послідовність пар <math>(X_1,Y_1), (X_2,Y_2),\ldots</math> надходять з виходу деякого пристрою спостереження. Такі пристрої присутні в задачах контролю (surveillance problems), управління (control operations) або втручання (intervention problems). У загальному випадку можна розглядати дані як часовий ряд. Оскільки непараметричні оцінки зазвичай визначаються по всій вибірці, її доводиться перераховувати при надходженні нових даних. Отже, з обчислювальної точки зору краще, щоб оцінка регресії, заснована на <math>(n + 1)</math> точках, будувалася виходячи з <math>(n + 1)</math> -го спостереження <math>(X_{n + i},Y_{n +1})</math> та оцінки, отриманої за першими <math>n</math> точками, без виклику попередніх даних з пам'яті комп'ютера.
−
оценка обычно определяется по всей выборке, ее приходится пересчитывать при поступлении новых данных. Следовательно, с вычислительной точки зрения предпочтительнее, чтобы оценка регрессии, основанная на <math>(n + 1)</math> точках, строилась исходя из <math>(n + 1)</math>-го наблюдения <math>(X_{n+i},Y_{n+1})</math> и оценки, полученной по первым <math>n</math> точкам, без вызова предыдущих данных из памяти компьютера.
 
  
−
=== Регрессограмма  ===
+
=== Регресограмма ===
−
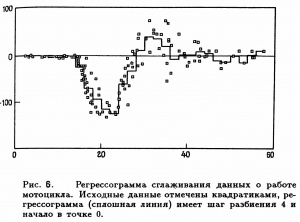
:Этот термин был введен Тьюки (Tukey, 1961) для того, чтобы подчеркнуть связь этой оценки с гистограммой. Регрессограмма представляет собой среднее тех значений переменных отклика, для которых соответствующие величины <math>X</math> попадают в один из интервалов разбиения пространства наблюдений переменной <math>X</math> Tukey(1947) - ее можно рассматривать как аппроксимацию <math>y(x)</math> ступенчатой функцией, и она фактически является ядерной оценкой (с прямоугольным ядром), вычисленной в средних точках интервалов разбиения. На '''Рис. 6.''' изображены данные о работе мотоцикла и регрессограмма при шаге разбиения 4.
+
: Цей термін був введений Тьюкі (Tukey, 1961) для того, щоб підкреслити зв'язок цієї оцінки з гістограмою. Регресограмма є середнім тих значень змінних відгуку, для яких відповідні величини <math>X</math> потрапляють в один з інтервалів розбиття простору спостережень змінної <math>X</math> Tukey (1947) - її можна розглядати як апроксимацію <math>y(x)</math> ступінчастою функцією, і вона фактично є ядерною оцінкою (з прямокутним ядром), обчисленої в середніх точках інтервалів розбиття. На '''Рис. 6.''' Зображені дані про роботу мотоцикла і регресограмма при кроці розбиття 4.
 +
 
 +
=== Медіанне згладжування ===
 +
[[Файл:300px-Example_med.jpg|300px|thumb|right|Рис. 7.  Медіанне згладжування]]
 +
:Припустимо, що метою апроксимації є крива умов медіани <math>med(Y|X = x)</math>, а не крива умовного середнього. Послідовність '''''"локальних медіан"''''' для значень змінної відгуку визначає э '''''медіанний згладжувач'''''. Медіанне згладжування зіграло важливу роль в історичному розвитку методів згладжування.
 +
 
 +
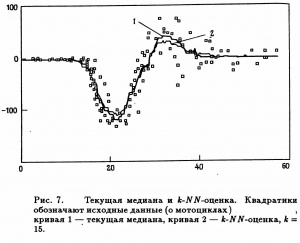
: Ця оцінка має очевидну аналогію з <math>k-NN</math> - оцінкою, але відрізняється, принаймні, у двох аспектах: медіанне згладжування стійке відносно великих викидів, і за допомогою цього методу з'являється можливість моделювати розриви кривої регресії <math> med(Y|X = x)</math>. На '''Рис. 7.''' На прикладі даних про мотоцикли ('''див. Пояснення до Рис. 5''') наведено порівняння двох методів оцінювання - медіанного згладжування і <math>k-NN</math> - оцінки.
 +
: Цей приклад виявляє властивість робастності медіанного згладжування. Медіанна оцінка не схильна до впливу групи можливих викидів в районі точки <math>x = 35 </math>, і вона трохи ближче до основної маси даних у двох '''''«областях сплесків»''''' <math>(x = 20,32)</math>. Деякий недолік полягає в тому, що за своєю природою оцінка медіанного згладжування є грубою характеристикою.
  
 
== Література ==
 
== Література ==
Рядок 95: Рядок 99:
 
# ''Расин,  Джеффри'' «Непараметрическая эконометрика:  вводный  курс». - Квантиль,  №4,  2008. - 7–56стр.
 
# ''Расин,  Джеффри'' «Непараметрическая эконометрика:  вводный  курс». - Квантиль,  №4,  2008. - 7–56стр.
  
−
== Ссилки ==  
+
== Посилання ==  
  
 
# ''Abramson,  I.S.'' On  bandwidth  variation  in  kernel  estimates  –  a  square  root  law.  Annals  of  Statistics 10. – 1982 . -  1217–1223 стр.
 
# ''Abramson,  I.S.'' On  bandwidth  variation  in  kernel  estimates  –  a  square  root  law.  Annals  of  Statistics 10. – 1982 . -  1217–1223 стр.
Рядок 111: Рядок 115:
 
# ''Tukey, J. W.'' Nonparametric estimation II. Statistically equivalent blocks and tolerance regions. The continuous case. Annals of Mathematical Statistics, 18.-1947. - 529-539 стр.
 
# ''Tukey, J. W.'' Nonparametric estimation II. Statistically equivalent blocks and tolerance regions. The continuous case. Annals of Mathematical Statistics, 18.-1947. - 529-539 стр.
  
−
==См. также==
+
==Див. також==
−
* [[Ядерное сглаживание]]
+
* [[Ядерне згладжуваня]]
−
* [[Регрессионный анализ]]
+
* [[Регресійний аналіз]]
−
—&nbsp;''[[Участник:Валентин Голодов|Валентин Голодов]] 18:37, 8 января 2010 (MSK)''
+
 
  
  
Рядок 171: Рядок 175:
  
 
==Посилання==
 
==Посилання==
 +
*[http://www.machinelearning.ru/wiki/index.php?title=%D0%9D%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F#.D0.9C.D0.B5.D0.B4.D0.B8.D0.B0.D0.BD.D0.BD.D0.BE.D0.B5_.D1.81.D0.B3.D0.BB.D0.B0.D0.B6.D0.B8.D0.B2.D0.B0.D0.BD.D0.B8.D0.B5/ Непараметрическая регрессия]

Поточна версія на 15:00, 13 березня 2012

{{{img}}}
Імя Володимир
Прізвище Шостак
По-батькові Михайлович
Факультет ФІС
Група СН-51
Залікова книжка СН-11-222


Непараметрична регресія, на відміну від параметричних підходів, використовує модель, яка не описується кінцевим числом параметрів.

Мета регресійного аналізу полягає у наступному, здійсненні розумної апроксимації невідомої функції відгуку [math]Y(X)[/math] по відомим точкам [math](X_i,Y_i)_{i = 1}^{m}[/math]. У випадку малих помилок спостереження стає можливим сконцентрувати увагу на важливих деталях середньої залежності [math]Y[/math] від [math]X[/math] при її інтерпретації.

Відмінність від параметричних підходів

Процедура апроксимації зазвичай називається згладжуванням. По суті ця апроксимація функції відгуку [math]Y[/math] може бути виконана двома способами. Досить часто використовується параметричний підхід, що полягає у припущенні, що функція відгуку [math]Y[/math] має деяку визначену функціональну форму, наприклад, це пряма лінія з невідомим вільним членом і нахилом. Альтернативою цьому може служити спроба оцінити [math]Y[/math] непараметричним чином, без вказівки конкретного її виду. Перший підхід до аналізу регресійної залежності називається параметричним, оскільки передбачається, що вид функції повністю описується кінцевим набором параметрів. Типовий приклад параметричної моделі є поліноміальне рівняння регресії, коли параметрами є коефіцієнти при невідомих. Однак при параметричному підході передбачається, що крива може бути представлена в термінах параметричної моделі, або, принаймні, є впевненість в тому, що помилка апроксимації для найкращого параметричного наближення є дуже малою. Навпаки, в непараметричної моделі регресійної залежності не проводиться проектування даних в "прокрустове ложе" фіксованої параметризації. Попереднє завдання параметричної моделі може виявитися занадто обмежувальним, або надто малої розмірності для апроксимації непередбачених характеристик, в той час, як непараметричне згладжування надає гнучкості засобам аналізу невідомих регресійних залежностей.
Непараметричний підхід приводить, таким чином, до гнучкого функціонального виду кривої регресії.

Різновиди

Ядерне згладжування

Одним із найпростіших методів є ядерне згладжування. Цей метод простий у застосуванні, не вимагає додаткових математичних відомостей і зрозумілий на інтуїтивному рівні. Ядерне згладжування в багатьох випадках є підходящим засобом. Існують різноманітні альтернативні методи згладжування такі, наприклад, як сплайни, але в [Хардле В., Заг 3] показується, що в асимптотичному сенсі вони еквівалентні ядерному згладжуванню.
Ключем до проведення якісного непараметричного оцінювання є вибір відповідної ширини вікна для наявного завдання. Хоча ядерна функція [math]K[/math] залишається важливою, її головна роль полягає в забезпеченні диференцієваності і гладкості отримуваної оцінки. Ширина вікна [math]h[/math], з іншого боку, визначає поведінку оцінки в кінцевих вибірках, що ядерна функція зробити просто не в змозі. Існують чотири загальні підходи до вибору ширини вікна:
  1. референтні евристичні правила;
  2. методи підстановки;
  3. методи крос-валідації;
  4. бутстаповскі методи.

Заради об'єктивності підкреслимо, що подані дані методи вибору ширини вікна [math]h[/math] не завжди гарантують гарний результат.

Виходячи з мінімізації глобальної помилки потрібно [math]h[/math] брати рівним:
[math]h_{opt}=\[ \frac{\int{K^2(z)dz}}{ \(\int{z^2K^2(z)dz} \)^2 \int{\[y''(x)\]^2dx} }\]^{-1/5} m^{-1/5}[/math], де [math]y(x)[/math] - невідома апроксимируюча залежність.

Референтні евристичні правила

Референтні евристичні правила вибору ширини вікна використовують стандартне сімейство розподілів для визначення [math]h_{opt}[/math].

Розглянемо оцінку Парзена-Розенблата для одновимірної функції щільності

[math]\hat{y}(x)=\frac{1}{mh} \sum_{i=0}^m{K\( \frac{X_i-x}{h}\)}[/math].
У випадку сімейства нормальних розподілів і гаусівського ядра [math]h_{opt}=1.059*\sigma m^{-1/5}[/math]. На практиці застосовується [math]\hat{\sigma}[/math], вибіркове стандартне відхилення.

Методи підстановки

Методи підстановки, такі як в Sheather, Jones (1991), полягають у підстановці оцінок невідомої константи [math]\int{\[y''(x)\]^2dx[/math] в формулу для оптимальної ширини вікна на основі первинної оцінки [math]y''(x)[/math], яка в свою чергу заснована на «попередній» ширині вікна, наприклад, знайденої за правилом [math]1.059*\sigma m^{-1/5}[/math] . Всі інші константи у виразі для [math]h_{opt}[/math] відомі після вибору ядерної функції [math]K[/math] (отже [math]\int{K^2(z)dz}[/math] і [math]\int{z^2K^2(z)dz}[/math] відомі). Хоча такі правила популярні, зацікавлений читач може звернутися до праць Loader (1999), де обговорюються відносні переваги методів підстановки в порівнянні з іншими методами вибору ширини вікна, обговорюваними нижче.

Методи крос-валідації

Методи крос-валідації засновані на основі найменших квадратів – це повністю автоматичний і диктуються даними методу вибору згладжуваного параметра. Цей метод заснований на принципі вибору ширини вікна, мінімалізує інтегральну средньоквадратичну помилку отримуваної оцінки. Інтеграл квадрата різниці [math]y(x)[/math] и [math]\hat{y}(x)[/math] має вигляд
[math]\int{\[y(x) - \hat{y}(x)\]^2dx } = \int{y^2(x)dx} - 2*\int{y(x)\hat{y}(x)dx} + \int{\hat{y}^2(x)dx}[/math]
Рис. 1. Оцінка щільності правила підстановки крос-валідаціїна на основі найменших квадратів
Можна замінити ці величини їх вибірковими аналогами, зробити поправку на зсув і отримати цільову функцію, яку потім можна мінімізувати за допомогою чисельних методів. Цей підхід був запропонований в роботах Rudemo (1982) і Bowman (1984). Для розуміння сутності коментарів у Loader (1999) на Рис. 1 зображені оцінки бімодальної щільності - ядерна оцінка при застосуванні правила підстановки і крос-валідації на основі найменших квадратів. Рис. 1показує, що насправді правило підстановки надмірно згладжує, приводячи до істотного зсуву в лівій вершині. Крос-валідація на основі найменших квадратів виправляє це, як зазначає Loader (1999), але ціною додаткової варіації в правій вершині.
Одна з проблем даного підходу - його чутливість до наявності округлених або Дискретизований даних, а також до дрібномасштабних ефектів у даних.
З прикладу випливає, що, можливо, ядерну оцінку з фіксованим параметром [math]h[/math] можна поліпшити, і існують «адаптивні» ядерні оцінки, які дозволяють [math]h[/math] змінюватися в точці [math]x[/math] або [math]X_i[/math]; див. Abramson (1982) і Breiman, Meisel, Purcell (1977). Ці оцінки, однак, сприяють введенню помилкового шуму в оцінку щільності. Однак метод з фіксованим [math]h[/math] домінує в прикладних дослідженнях.

Бутстраповскі методи

Faraway, Jhun (1990) запропонували метод вибору ширини вікна [math]h[/math] на основі бутстрапа, шляхом оцінювання інтегральної середньоквадратичної помилки для кожної фіксованої ширини вікна, і потім мінімізації її по всіх значеннях. Даний підхід використовує згладжений бутстраповский метод на основі початкової оцінки щільності. Один з недоліків цього підходу в тому, що цільова функція є випадковою, що може привести до проблем при чисельній мінімізації, а також її обчислювальної складністі.

Ядерні ваги визначають деяку ділянку навколо точки [math]x[/math] що лежить на сітці. Наступне питання згладжування - поліноміальні наближення функції [math]y[/math] в цій ділянці.

Локально поліноміальні наближення

Рис. 2. Локально поліноміальні згладжування
Найпростішим поліномом наближення в такій околиці є константа. Ядерна оцінка мінімізує суму квадратів неув'язок в околиці точки [math]x[/math], форма і розмір якої визначається ядром [math]K[/math].
Локально поліноміальні наближення і їх зв'язок з ядерним згладжуванням детально досліджені в працях (Muller 1987), де показана їх еквівалентність.
Детальніше також див. Алгоритм LOWESS

k-NN оцінки

Рис. 3. k-NN згладжування
Конструкція оцінок найближчих сусідів відрізняється від ядерних оцінок. Ядерна оцінка визначається як зважене середнє змінних відгуку у фіксованій ділянці точки [math]x[/math], причому ваги визначалися ядром [math]K[/math] і шириною вікна [math]h[/math]. Оцінка k-найближчих сусідів є середнім, зваженим в мінливих ділянках. Ця ділянка визначається тільки тими значеннями змінної [math]X[/math], які в [math]k[/math] є найближчими до [math]x[/math] за евклідом (звичайної) віддалі. Послідовність [math]k-NN[/math] ваг була введена в роботі Loftsgaarden, Quesenberry (1965) для близької задачі оцінювання щільності і використовувалася в Cover, Hart (1967) для цілей класифікації.
Параметр згладжування [math]k[/math] визначає ступінь гладкості оцінки кривої. Він грає ту ж роль, що і ширина вікна для ядерних згладжувань. Вплив змінного [math]k[/math] на якісні характеристики оцінки аналогочно випадку ядерних оцінок з прямокутним ядром.
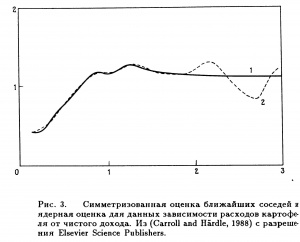
На Рис. 3. Зображений приклад порівняння ядерного згладжування з квартіческім ядром і [math]k-NN[/math] згладжування. Ширина вікна вибиралася методом крос-перевірки. Дані пропускались через вікна шириною [math]h = 0.25[/math] для ядерного згладжування на відрізку [math][0,3][/math] і [math]h = 0.15[/math] для осі значень. Отримані криві регресії практично збігаються для [math]x\le 1[/math], де лежить велика частина даних. При більших значеннях [math]x[/math] спостерігається істотна розбіжність кривих: ядерна оцінка показує очевидне бімодальне співвідношення, а симетризована оцінка найближчих сусідів вказує або на асимптоту, або навіть на слабке спадання із зростанням доходу. В контексті завдання, здається, що останнє містить більше сенсу з точки зору економіки ...

Оцінки ортогональних розкладань

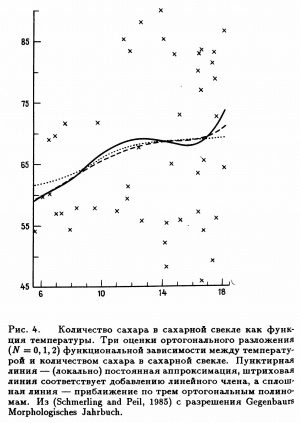
Рис. 4. Згладжування з допомогою ортогональних розкладань

Припустимо, що функція регресії може бути представлена у вигляді ряду Фур'є

[math]y(x)=\sum_{j=0}^{\infty}\beta_j\varphi_j(x)[/math],
де [math]{\{\varphi_j\}}_{j=0}^\infty[/math] - відома система базисних функцій, а [math]{\{\beta_j\}}_{j=0}^\infty[/math] - невідомі коефіцієнти Фур'е. В работі Szego (1959) наведені умови, за яких таке подання можливе. Добре відомими системами базисних функцій є поліноми Лагерра та поліноми Лежандра. Як тільки фіксований базис функцій, проблема оцінювання функції регресії може бути зведена до оцінювання коефіцієнтів Фур'є. Звичайно, існує певна складність, яка полягає в тому, що може бути нескінченно багато ненульових коефіцієнтів [math]\beta_j[/math]. Таким чином, при заданому кінцевому обсязі вибірки [math]m[/math] можна ефективно оцінити лише підмножину коефіцієнтів.
Приклад застосування показаний на 'Рис. 4. '

Згладжування сплайнами

Рис. 5. Згладжування за допомогою сплайнів

Загальною мірою близькості до даних для деякої кривої [math]g[/math] є сума квадратів нев'язок

[math]\sum_{i=1}^{n}{(Y_i-g(X_i))}^2[/math]
Якщо [math]g[/math] може будь кривою - необмеженої в функціональному сенсі - то цей захід, що має сенс відстані, дорівнює нулю для всякої кривої [math]g[/math], інтерполюється дані. Підхід, заснований на згладжуванні сплайнами, виключає цю небажану інтерполяцію даних за рахунок досягнення компромісу між двома суперечливими цілями: отримати гарну апроксимацію даних і отримати криву, яка не має надто швидких локальних змін.
Відомі різні способи кількісної оцінки локальних змін. Можна визначити міру плавності кривої, засновану, наприклад, на першій, другій, і більш старших похідних. Для успішного розкриття основної ідеї найзручніше ввести інтеграл від квадрата другої похідної, тобто для кількісної оцінки локального зміни використовувати штраф за порушення плавності
[math]\int {(g''(x))}^2dx[/math].
Приклад згладжування сплайнами представлений на Рис. 5.Інтерпретація даних: дані про мотоциклі [Значення [math]X[/math] (в мс) після змодельованого зіткнення з мотоциклом. Мінлива відгуку [math]Y[/math] - прискорення (в g) посмертного тестування об'єкта. З Schmidt, Mattern, Schiiler (1981)]

Перелік менш поширених методів

Рис. 6. Регрессограмма

Рекурентні методи

Припустимо, що дані [math]\{(X_i,Y_i)\}_{i\ ge l}[/math] спостерігаються не як вибірка фіксованого обсягу [math]m[/math], а як послідовність пар [math](X_1,Y_1), (X_2,Y_2),\ldots[/math] надходять з виходу деякого пристрою спостереження. Такі пристрої присутні в задачах контролю (surveillance problems), управління (control operations) або втручання (intervention problems). У загальному випадку можна розглядати дані як часовий ряд. Оскільки непараметричні оцінки зазвичай визначаються по всій вибірці, її доводиться перераховувати при надходженні нових даних. Отже, з обчислювальної точки зору краще, щоб оцінка регресії, заснована на [math](n + 1)[/math] точках, будувалася виходячи з [math](n + 1)[/math] -го спостереження [math](X_{n + i},Y_{n +1})[/math] та оцінки, отриманої за першими [math]n[/math] точками, без виклику попередніх даних з пам'яті комп'ютера.

Регресограмма

Цей термін був введений Тьюкі (Tukey, 1961) для того, щоб підкреслити зв'язок цієї оцінки з гістограмою. Регресограмма є середнім тих значень змінних відгуку, для яких відповідні величини [math]X[/math] потрапляють в один з інтервалів розбиття простору спостережень змінної [math]X[/math] Tukey (1947) - її можна розглядати як апроксимацію [math]y(x)[/math] ступінчастою функцією, і вона фактично є ядерною оцінкою (з прямокутним ядром), обчисленої в середніх точках інтервалів розбиття. На Рис. 6. Зображені дані про роботу мотоцикла і регресограмма при кроці розбиття 4.

Медіанне згладжування

Рис. 7. Медіанне згладжування
Припустимо, що метою апроксимації є крива умов медіани [math]med(Y|X = x)[/math], а не крива умовного середнього. Послідовність "локальних медіан" для значень змінної відгуку визначає э медіанний згладжувач. Медіанне згладжування зіграло важливу роль в історичному розвитку методів згладжування.
Ця оцінка має очевидну аналогію з [math]k-NN[/math] - оцінкою, але відрізняється, принаймні, у двох аспектах: медіанне згладжування стійке відносно великих викидів, і за допомогою цього методу з'являється можливість моделювати розриви кривої регресії [math]med(Y|X = x)[/math]. На Рис. 7. На прикладі даних про мотоцикли (див. Пояснення до Рис. 5) наведено порівняння двох методів оцінювання - медіанного згладжування і [math]k-NN[/math] - оцінки.
Цей приклад виявляє властивість робастності медіанного згладжування. Медіанна оцінка не схильна до впливу групи можливих викидів в районі точки [math]x = 35[/math], і вона трохи ближче до основної маси даних у двох «областях сплесків» [math](x = 20,32)[/math]. Деякий недолік полягає в тому, що за своєю природою оцінка медіанного згладжування є грубою характеристикою.

Література

  1. Хардле В. непараметрическая регрессия.- 1989.
  2. Расин, Джеффри «Непараметрическая эконометрика: вводный курс». - Квантиль, №4, 2008. - 7–56стр.

Посилання

  1. Abramson, I.S. On bandwidth variation in kernel estimates – a square root law. Annals of Statistics 10. – 1982 . - 1217–1223 стр.
  2. Bowman, A.W. An alternative method of cross-validation for the smoothing of density estimates. Biometrika 7. - 1984 . - 353 –360 стр.
  3. Breiman, L., W. Meisel, E. Purcell Variable kernel estimates of multivariate densities. Technometrics 19. - 1977 . - 135 –144 стр.
  4. Cover, T. M. and Hart, P. E. Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13. - 1967 . - 21 -27 стр.
  5. Faraway, J., M. Jhun Bootstrap choice of bandwidth for density estimation. Journal of the American Statistical Association 85.- 1990.-1119–1122 стр.
  6. Loader, C.R.Bandwidth selection: Classical or plug-in? Annals of Statistics 27.-1999. - 415–438 стр.
  7. Loftsgaarden, D. O., Quesenberry, G. P. A nonparametric estimate of a multivariate density function. Annals of Mathematical Statistics, 36.-1965.-1049-1051 стр.
  8. Muller H. G. Weighted local regression and kernel methods for nonparametric curve fitting. Journal of the American Statistical Association, 82.-1987.-231-238 стр.
  9. Rudemo, M. Empirical choice of histograms and kernel density estimators. Scandinavian Journal of Statistics 9.-1982. -65–78 стр.
  10. Schmidt, G. Mattern, R., Schiiler, F. Biomechanical investigation to determine physical and traumatological differentiation criteria for the maximum load capacity of head and vertebral column with and without protective helmet under effects of impact. EEC Research Program on Biomechanics of Impacts. Final Report Phase III, Project 65, Institut fur Rechtsmedizin, Universitat Heidelberg, West Germany.-1981.- 231-238 стр.
  11. Sheather, S., M. Jones A reliable data-based bandwidth selection method for kernel density estimation. Journal of Royal Statistical Society, Series B 53.-1991. - 683–690 стр.
  12. Szego, G. Orthogonal polynomials. Amer. Math. Soc. Coll. PubL, 23.-1959.
  13. Tukey, J. W. Nonparametric estimation II. Statistically equivalent blocks and tolerance regions. The continuous case. Annals of Mathematical Statistics, 18.-1947. - 529-539 стр.

Див. також

Посилання

Отримано з https://wiki.tntu.edu.ua/index.php?title=Непараметрична_регресія&oldid=14006