Рух твердого тіла в рідині
Одним із найважливіших завдань аеро- і гідродинаміки є дослідження руху твердих тіл в газах і рідинах, зокрема вивчення тих сил, з якими середовище діє на рухоме тіло. Ця проблема набула особливо великого значення у зв'язку з бурхливим розвитком авіації і збільшенням швидкості руху морських суден.
Зміст
В'язкість
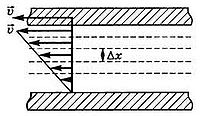
У всіх реальних рідинах при переміщенні одних верств щодо інших виникають більш-менш значні сили тертя. З боку шару, що рухається швидше, на шар, що рухається повільніше, діє сила прискорення. З боку ж шару, що рухається повільніше, на шар, що рухається швидше, діє гальмівна сила. Це внутрішнє тертя називається в'язкістю рідини чи газу. Ці сили спрямовані по дотичній до поверхні шарів. Нехай між двома площинами знаходиться шар рідини; верхня площина рухається щодо нижньої зі швидкістю [math]\vec v[/math]. Розіб'ємо рідину на дуже тонкі шари паралельними площинами, віддаленими на відстані Δx один від одного. Шари рідини, що дотикаються до твердих тіл, прилипають до них. Проміжні шари мають розподіл швидкостей, зображений на рисунку. Нехай різниця швидкостей між сусідніми шарами [math]~\Delta \vec \upsilon[/math]. Величина [math]~\frac{\Delta \upsilon}{\Delta x}[/math], яка показує, як швидко змінюється швидкість при переході від шару до шару, називається градієнтом швидкості.
Розрахунки показують, що сила внутрішнього тертя між сусідніми шарами рідини тим більша, чим більша площа поверхні зіткнення шарів, і залежить від швидкості зміни швидкості при переході від шару до шару в напрямку осі Ox, перпендикулярної до швидкості руху шарів:
де S - площа зіткнення шарів, η - коефіцієнт внутрішнього тертя, або в'язкість рідини, [math]~\frac{\Delta \upsilon}{\Delta x}[/math] - градієнт швидкості. В'язкість залежить від температури. З ростом температури в'язкість рідини зменшується.
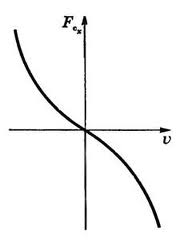
При русі твердого тіла в рідині або газі також виникає сила опору руху, яку називають силою в'язкого тертя. Але на відміну від сухого тертя в рідинах і газах відсутня сила тертя спокою. Наявність сили опору руху тіла в середовищі пояснюється існуванням внутрішнього тертя, обумовленого відносним рухом шарів рідини чи газу. Встановлено, що сила в'язкого тертя залежить від швидкості руху тіла. Залежність проекції сили в'язкого тертя від швидкості показана на малюнку
Якщо швидкість руху тіла невелика, то сила опору прямо пропорційна модулю швидкості: [math]F_c = kυ[/math], де [math]k[/math] - коефіцієнт пропорційності, який залежить від виду в'язкого середовища, форми і розмірів тіла. Якщо швидкість руху тіла зростає, то зростає і сила опору:
[math]F_c = k \upsilon^n[/math], де [math]n = 2,3[/math]
При збільшенні швидкості руху тіла в рідині або газі з'являються вихори, які гальмують рух: внаслідок в'язкості в області, прилеглій до поверхні тіла, утворюється примежовий шар частинок, що рухаються з меншими швидкостями. В результаті гальмуючої дії цього шару виникає обертання частинок, і рух рідини в примежовому шарі стає вихровим. Якщо тіло не має обтічної форми, то примежовий шар рідини відривається від поверхні тіла. За тілом виникає потік рідини (газу), спрямований протилежно до набігаючого потоку. Примежовий шар, який відірвався слідуючи за цією течією, утворює вихори, що обертаються в протилежні сторони, (рис.б). Рідина, що обертається у вихорі, рухається швидше ніж рідина в стаціонарному потоці (рис.а). Тому з задньої сторони обтічного тіла, де утворилися вихори, тиск стає меншим, ніж з передньої. Різниця тисків попереду і позаду рухомого тіла і створює опір руху тіла. У підсумку із збільшенням швидкості сила опору зростає нелінійно
Сила опору залежить від форми тіла. Надання тілу спеціально розрахованої обтічної форми істотно зменшує силу опору, так як в цьому випадку рідина всюди прилягає до його поверхні і не завихрюється позаду нього (рис.в).
Рух тіла у нев’язкій рідині
При русі твердого тіла в нев'язкій рідині на нього діють гідродинамічні сили тиску. Нехай тверде тіло рухається з постійною швидкістю [math]\vec v_0[/math] в нев'язкій безмежній рідині. Щоб спростити рішення задачі, слід використати принцип обернення руху. Тоді тіло буде представлятися нерухомим, а рідина - натікаючою на нього зі швидкістю [math]\vec v_0[/math]. У кожній точці потоку швидкість з часом змінюватися вже не буде, тобто рух рідини стане сталим (рис. 3.10). У силу умови плавного обтікання поверхнею тіла є поверхня потоку, що складається із сукупності ліній потоку, до кожної з яких можна застосувати інтеграл Бернуллі. Оскільки розглядаємо безмежну рідину, гідростатичним тиском цікавитися не будемо і розглянемо розподіл надлишкового тиску по відношенню до гідростатичного.
Тоді для точки, розміщеної далеко перед тілом, де на потік не впливає присутність тіла, швидкість рівна [math]\vec v_0[/math], а тиск – <[math]p_{0}[/math], а для точки на поверхні тіла, дешвидкість рівна [math]\vec v_1[/math], а тиск – [math]p_{1}[/math] маємо:
[math]p_{0}+\frac{1}{2}\rho \upsilon _{0}^{2}=p_{1}+\frac{1}{2}\rho \upsilon _{1}^{2}[/math]
Звідси тиск в довільній точці поверхні тіла (3.10):
[math]p_{1}=p_{0}+\left ( 1-\frac{\nu _{1}^{2}}{\upsilon _{0}^{2}} \right )\frac{\rho \upsilon _{0}^{2}}{2}[/math]; або [math]p_{1}-p_{0}=c_{p} \frac{\rho \upsilon_{0}^{2}}{2}[/math]
Величину [math]\rho \upsilon _{0}^{2}/2[/math] називають швидкісним напором
Величина [math]c_{p}[/math] називають коефіцієнтом тиску. Зручність використання цього коефіцієнта полягає в тому, що він не залежить від виду рідини, а отже, епюра [math]c_{p}[/math] визначається лише формою тіла. Це значить, що її можна отримати, моделюючи, обтікання тіла водою обтіканням його повітряним потоком в аеродинамічній трубі, що зазвичай технічно простіше і точніше.
Рух тіла у в’язкій рідині
У в’язкій рідині до сили тиску додаються сили, які обумовлені дотичними напруженнями, які можна представити у вигляді:
[math]\vec{\tau }=\tau _{0}\vec{\l}[/math] ,
де [math]\vec{l}[/math]– вектор дотичної до елементарної площі [math]dS[/math] на поверхні тіла. Тоді головний вектор гідродинамічних сил, які діють на поверхню [math]S[/math] тіла, яке рухається у в’язкій рідині:
[math]\vec{R}=-\int_{S}p\vec{n} dS+\int_{S}\tau _{0}\vec{l}dS[/math]
Розподіл тиску по поверхні тіла зручно виражати через безрозмірний коефіцієнт тиску і швидкісний напір [math]\rho \upsilon _{0}^{2}/2[/math] відповідно до рівняння (3.10). Вводиться поняття коефіцієнта місцевого тертя
[math]c_{\tau }=\frac{\tau _{0}}{\rho \upsilon _{0}^{2}/2}[/math] ,
який також є безрозмірною величиною. Позначивши через [math]S_{0}[/math] деяку характерну площу, формулу (3.19) можна записати у вигляді:
[math]\vec{R}=\frac{\rho \upsilon_{0}^{2}}{2}S_{0}\left ( -\int_{S} c_{p}\vec{n}\frac{dS}{S_{0}} +\int_{S} c_{\tau }\vec{l} \frac{dS}{S_{0}} \right )[/math] ,
де множник [math]\frac{1}{2}\rho \upsilon _{0}^{2}S_{0}[/math] має розмірність сили, а безрозмірний векторний вираз в дужках називається коефіцієнтом гідродинамічної сили:
[math]\vec{c}_{R}=-\int_{S} c_{p}\vec{n}\frac{dS}{S_{0}} +\int_{S} c_{\tau }\vec{l} \frac{dS}{S_{0}}=\vec{c}_{Rp}+\vec{c}_{R\tau }[/math]
де [math]\vec{c}_{Rp}[/math] – коефіцієнт тиску, [math]\vec{c}_{R\tau }[/math] – коефіцієнт тертя.
В результаті структурний вираз для гідродинамічної сили, яка діє на тіло запишемо у вигляді:
[math]\vec{R}=\vec{c}_{R}\frac{\rho \upsilon _{0}^{2}}{2}S_{0}[/math]
де [math]\vec{c}_{M}[/math] – коефіцієнт моменту, [math]L[/math] – характерний лінійний розмір.
В більшості випадків гідродинамічний розрахунок або експеримент зводится до визначення безрозмірних коефіцієнтів [math]\vec{c}_{R}[/math] i [math]\vec{c}_{M}[/math]
Несталі руху тіл в рідині. Узагальнені приєднані маси
При несталих рухах тіла змінюється кінетична енергія рідини за рахунок зміни швидкостей рідких частинок, викликаних рухом тіла. Кінетична енергія елементарної рідкої частинки об’ємом [math]dV[/math]
[math]dT=\left ( \rho \upsilon ^{2}/2 \right )dV[/math]
де [math]\upsilon[/math] – швидкість частинки. У випадку безвихрового руху ідеальної рідини швидкість визначається через потенціал швидкості. Для всієї маси рідини, яка оточує тіло, кінетична енергія:
[math]T=\int_{V}\frac{\rho \upsilon ^{2}}{2}dV[/math]
Якщо рідина безмежна, то [math]V \to \propto[/math] , але [math]T[/math] залишається кінцевою величиною, оскільки по мірі віддалення від тіла рух сповільнюється, а швидкості рідких частинок прямують до нуля.
Можна розглянути частинний випадок прямолінійного несталого руху тіла. Нехай [math]\upsilon _{0}\left ( t \right )[/math] – швидкість тіла. Кінетична енергія представиться у вигляді:
[math]T=\frac{\upsilon _{0}^{2}}{2}\int_{V}\rho \left ( \frac{\upsilon }{\upsilon _{0}} \right )^{2}dV=\lambda _{0}\frac{\upsilon _{0}^{2}}{2}[/math];
де
[math]\lambda _{0}=\int_{V}\rho\left ( \upsilon /\upsilon _{0} \right )^{2}dV[/math].
Величина [math]\lambda _{0}[/math] має розмірність маси, і вона, в силу скінченності [math]T[/math], скінченна, якщо навіть [math]V \to \propto[/math]. Таким чином, кінетична енергія всієї рідини, що оточує тіло, може бути представлена як кінетична енергія деякого кінцевого об'єму рідини, що має масу [math]\lambda _{0}[/math] і рухається зі швидкістю, що дорівнює швидкості центру маси тіла.
Знаючи кінетичну енергію, можна визначити силу, що діє на тіло з боку рідини. Позначимо її [math]R_{u}[/math]. З курсу теоретичної механіки відомо, що зміна кінетичної енергії рідини дорівнює роботі сили, що діє на рідину з боку тіла на розглядуваній ділянці шляху: [math]dT=-R_{u}ds[/math], Де [math]ds[/math] - елемент шляху, пройденого тілом.
Таким чином [math]R_{u}=-\frac{dT}{ds}=\frac{dT}{dt}\cdot \frac{dt}{ds}=-\frac{1}{\upsilon _{0}}\frac{dT}{dt}[/math]
або з урахуванням формули (3.20)
[math]R_{u}=-\frac{1}{\upsilon _{0}} \cdot 2\left ( \frac{\upsilon _{0}\lambda _{0}}{2} \right )\frac{d\upsilon _{0}}{dt}=-\lambda _{0}\frac{d\upsilon _{0}}{dt}[/math]
Отже, при несталому русі тіла в нев'язкій рідині на нього діє гідродинамічна сила інерції, пропорційна прискоренню тіла. При русі тіла з постійною швидкістю [math]d\upsilon _{0}/dt=0[/math] і інерційна сила відсутня.
Якщо тверде тіло, що має масу [math]m[/math], під дією деякої зовнішньої сили [math]\vec{R}_{zovn}[/math] (наприклад, тяги гвинта) рухається з прискоренням [math]d\vec{\upsilon }_{0}/dt[/math] у порожнечі, то рівняння його руху має вигляд
[math]m\frac{d\vec{\upsilon }_{0}}{dt}=\vec{R}_{zovn[/math]
При русі тіла в рідині на нього діє додаткова гідродинамічна сила (3.21). Тоді рівняння руху тіла
[math]\left ( m+\lambda _{0} \right )\frac{d\vec{\upsilon }_{0}}{dt}=\vec{R}_{zovn}[/math]
Значить, в рівнянні несталого руху тіла в рідині для обліку реакції рідкого середовища необхідно масу тіла збільшити на додаткову масу, яку називають приєднаною масою рідини. Не слід розуміти цю масу буквально як масу рідини, яка рухається разом з тілом. Це характеристика інерції рідини, оточуючої тіло, при його русі із змінною швидкістю. Ми розглянули найпростіший випадок несталого руху тіла - поступального в певному напрямку. При інших більш складних видах руху тіл (поступальний в різних напрямках, обертальні, їх комбінації) гідродинамічні реакції інерційної природи характеризуються узагальненими приєднаними масами - не тільки масами, але і статичними моментами і моментами інерції цих мас. У загальному випадку несталого руху тіла з шістьма ступенями свободи існує 36 узагальнених приєднаних мас. При русі тіла в безмежній рідині вони залежать тільки від форми тіла та напрямку руху, а при русі по або поблизу вільної по- верхности рідини ще й від параметрів хвиль, викликаних рухом тіла (Зокрема, від їх частоти) / 10, 14, 15 /.
Джерела та посилання
1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 108-110.
2. Основы гидродинамики : учеб. пособие / С. Д. Чижиумов. – Комсомольск-на-Амуре : ГОУВПО «КнАГТУ», 2007. − 55 с.
3. [[1]] - Трение при движении твёрдого тела в жидкости.