Гідростатичний тиск і його властивості

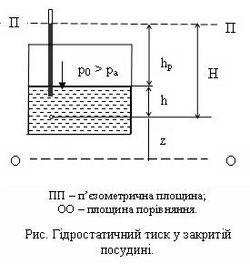
Гідростатичний тиск [math]p[/math] (рос.гидростатическое давление, англ. hydrostatic pressure, нім. Wasserdruckhöne f) - це напруга стиску в точці, розміщеній всередині рідини, що знаходиться в стані спокою:

[math]\ p = \lim_{\Delta \omega\to\0}\frac{{\Delta \ P}}{{\Delta \omega}}[/math],

де [math]\Delta \ P[/math] - сила тиску, що діє на елементарну площинку [math]\Delta \omega[/math], яка включає в соі дану точку.

На зовнішній поверхні рідини гідростатичний тиск завжди спрямований по нормалі до площини, на яку він діє, а в будь-якій точці всередині рідини його величина не залежить від орієнтації площинки в просторі. Він є лише функцією координат.

У міжнародній системі одиниць фізичних величин (СІ) одиницею вимірювання тиску є 1 H/м² - паскаль (Па). Зручнішим для використання є кратні одиниці - гектопаскаль (гПа), кілопаскаль (кПа) і мегапаскаль (МПа): 1 гПа = 100 Па, 1 кПа = 1000 Па, 1 МПа = 10⁶ Па.

Властивості гідростатичного тиску

Рис. Перша Властивість гідростатичного тиску

Властивість 1

Гідростатичний тиск завжди спрямований до площини, на яку він діє, по внутрішній нормалі.

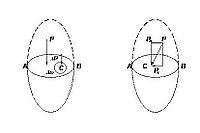
Розглянемо силу гідростатичного тиску [math]p[/math], прикладену в точці С під кутом до поверхні А - В об'єму рідини, який знаходиться в стані рівноваги (рис.).Цю силу можна розкласти на: нормальну силу [math]P_n[/math] і дотичну силу [math]P_t[/math] до поверхні А - В. Отже, сила гідростатичного тиску [math]p[/math] в точці С діє лише в напрямку сили [math]P_n[/math], тобто нормально до поверхні А - В.Направлена вона тільки по внутрішній нормалі. При представлені направленні сили гідростатичного тиску по зовнішній нормалі виникнуть розтягуючі сили, що призведе до руху рідини. Це перечить умові, за якою рідина має знаходитись у стані спокою.Тому сила гідростатичного тиску завжди стискуюча, тобто направлена по внутрішній нормалі.

Властивість 2

Рис. Друга Властивість гідростатичного тиску

Гідростатичний тиск не залежить від кута нахилу площини дії і в різних напрямках одинаковий за величиною.

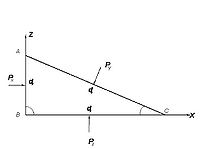
Щоб довести другу властивість гідростатичного тиску виділимо в рідині, яка знаходиться в стані рівноваги, частинку в формі трикутної призми з основою у вигляді прямокутного трикутника А - В - С. Будемо розглядати цей об'єм в довільній системі координат X, Y, Z. При цьому вісь yперпендикулярна площині. На призму діють такі сили: [math]P_x[/math], [math]P_y[/math], [math]P_z[/math], [math]P_e[/math], а також сила тяжіння G, яка дорівнює [math]gdxdydz/2[/math].

[math]P_x=p_xdzdy[/math]

[math]P_z=p_zdxdy[/math]

[math]P_e=p_ededy[/math]

Силою тяжіння можна знехтувати, оскільки ця величина буде 3-го порядку малості, а сили які діють на грані призми будуть 2-го порядку. Якщо частина рідини знаходиться в стані рівноваги, то сума проекції всіх сил, прикладених до неї, в будь-якому напрямку дорівнюватиме нулю:

[math]\sum\ x=0[/math] [math]p_xdzdy-p_ededy\sin\alpha[/math]

[math]\sum\ z=0[/math] [math]p_zdxdy-p_ededy\cos\alpha[/math]

Підставивши [math]dz=de\sin\alpha[/math] і [math]dx=de\cos\alpha[/math] в попереднє рівняння і поділивши кожне рівняння на [math]dy[/math], отримаємо:

[math]\sum\ x=0[/math] [math]p_xdz-p_edz=0[/math]

[math]\sum\ z=0[/math] [math]p_zdx-p_edx=0[/math]

Звідки: [math]p_x=p_z=p_e[/math]

Отже, гідростатичний тиск на нахилену грань [math]p_e[/math] рівний по велечині з гідростатичним тиском на вертикальну і горизонтальні грані. Оскільки кут нахилу грані взятий довільно, то можна стверджувати, що гідростатичний тиск в будь-якій точці рідини діє однаково у всіх напрямках.