Рівняння Бернуллі для потоку реальної рідини
Рівня́ння Берну́ллі (рос. уравнение Бернулли; англ. Bernoulli's theorem; нім. Bernulligleichung) — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю [math]v[/math] рідини, тиском [math]p[/math] в ній та висотою [math]h[/math] частинок над площиною відліку.Рівняння Бернуллі є наслідком закону збереження енергії. Якщо рідина не ідеальна, то її механічна енергія розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає.Рівняння Бернуллі широко застосовують для розв'язання багатьох гідравлічних задач у нафтогазовій справі. Виведене Данилом Бернуллі в 1738 р.
Зміст
Історична довідка
Данило Бернуллі - видатний швейцарський фізик-універсал і математик, син Йоганна Бернуллі, один з творців кінетичної теорії газів, гідродинаміки і математичної фізики.Народився 8 лютого 1700 у Гронінгені. Закінчив Базельську гімназію, за настановою батька вивчав медицину. Вчився в Гейдельберзі и Страсбурзі. В 1724 вийшов перший трактат Бернуллі по математиці. З 1725 по 1732 працював в Санкт-Петербурзькій академії наук – спочатку займався фізіологією, потім очолював кафедру математики. В l733 повернувся в Базель, де був професором анатомії і ботаніки, а потім філософії і фізики (з 1750). Внесок Д.Бернуллі в науку важко переоцінити. Разом з М.В. Ломоносовим він стояв біля витоків кінетичної теорії газів. У його працях можна знайти передбачення законів Гей-Люссака, Клайперона і Шарля. Бернуллі був першим, хто висловив думку про те, що тиск газу обумовлене тепловим рухом молекул. У гідродинаміці Д.Бернуллі дав рівняння сталого руху ідеальної нестисливої рідини. Воно виражає собою закон збереження енергії. В 1738 опублікував свою знамениту роботу «Гідродинаміка, або Записки про сили і рухи в рідинах» («Hydrodynamica, sive de viribus et motibus fluidorum commentarii»), у якій сформулював основи механіки рідини. У цьому творі Бернуллі вперше ввів поняття роботи і коефіцієнта корисної дії, записав рівняння стаціонарного руху ідеальної рідини (рівняння Бернуллі), виклав ідеї кінетичної теорії газів.Данила Бернуллі разом з Д'Аламбером, Л. Ейлером і Лагранжем можна вважати засновником математичної фізики. Також Д.Бернуллі ввів термін «гідродинаміка» для того, щоб об'єднати дві науки: гідростатику і гідравліку. Значний вклад вніс в математику. Займався розробкою чисельних вирішень алгебраїчних рівнянь, теорією рядів, теорією ймовірностей, дав спосіб вирішення ймовірнісних задач методами математичного аналізу. Був лауреатом почесних премій Паризької академії наук. Був членом Берлінської, Лондонської, Паризької, Санкт-Петербурзької академій наук. Рівняння Д.Бернуллі, отримане в 1738 р., є фундаментальним рівнянням гідродинаміки. Воно дає зв'язок між тиском , середньою швидкістю і п'єзометричного висотою в різних перерізах потоку і виражає закон збереження енергії рідини, що рухається.Основні поняття
- В'язкість
В’язкість рідин відноситься до головних факторів, які необхідно враховувати при русі рідин та розв’язуванні задач, пов’язаних з рухом рідин. Рідини, що існують в природі – це в більшій чи меншій мірі в’язкі рідини. Такі рідини в механіці рідини називаються реальними. Отже, реальні рідини мають в’язкість та за певних умов розширюються і стискаються
- Стисливість
Всі реальні рідини у тій чи іншій мірі стискаються, тобто під дією зовнішнього тиску зменшують свій об'єм. Стисливість – це здатність рідини змінювати свій об’єм при зміні тиску.
- Потік рідини
Потоком рідини в гідравліці називають масу рідини, обмежену твердими поверхнями, направляючими, поверхнями розділу рідин або вільними поверхнями.
- Динаміка реальної (в'язкої рідини)
Реальна рідина - модель природної рідини, що характеризується ізотропністю всіх фізичних властивостей, але на відміну від ідеальної моделі, володіє внутрішнім тертям при русі. При вивченні руху реальної (в'язкої рідини) можна піти двома різними шляхами: скористатися готовими диференціальними рівняннями і їхніми рішеннями, отриманими для ідеальної рідини. Облік прояви в'язких властивостей здійснюється за допомогою введення в рівняння додаткових поправочних членів рівняння, вивести нові рівняння для в'язкої рідини. Для практичної інженерної діяльності більш прийнятним слід вважати перший напівемпіричний шлях, другий слід використовувати лише в тих випадках, коли потрібно детальне вивчення процесу руху в'язкої рідини.
Виведення рівняння Бернуллі для потоку реальної рідини
Розглянемо стаціонарний потік в'язкої рідини, який будемо вважати за сукупність елементарних струминок.У потоці скінченних розмірів у кожній струминці висота положення, тиски й швидкості неоднакові у різних точках поперечного перерізу. Це означає, що частинки рідини в різних точках поперечного перерізу мають різну питому енергію. Інакше можна сказати, що кожна елементарна струминка в поперечному перерізі має свій повний напір :
[math]H=z+\frac{p}{\rho g}+\frac{{{u}^{2}}}{2g}[/math]
Енергію за одиницю часу, яку має рідина в елементарній струминці при площі живого перерізу [math]\omega[/math]d, можна записати так:
[math]\left( z+\frac{p}{\rho g}+\frac{{{z}^{2}}}{2g} \right)\rho gud\omega[/math]
Для того щоб визначити сумарну енергію потоку в будь якому живому перерізі, треба підсумувати енергію рідини в усіх елементарних струминках в даному поперечному перерізі.Отже, сумарна енергія рідини яка проходить через даний живий переріз потоку за одиницю часу, виразиться:
[math]\int\limits_{\infty }{\left( z+\frac{p}{\rho g}+\frac{{{u}^{2}}}{2g} \right)\rho gud\omega }[/math]
Питома енергія усього потоку Еп, який проходить через даний переріз за одиницю часу, визначиться як відношення всієї сумарної енергії потоку до кількості рідини, що протікає через цей же переріз і за цей час, тобто
[math]En=\frac{\int\limits_{\infty }{\left( z+\frac{p}{\rho g}+\frac{{{u}^{2}}}{2g} \right)\rho gud\omega }}{\int\limits_{\infty }{\rho gud\omega }}[/math]
Позаяк при паралельно-струминному або плавно-змінному русі в будь-якому живому перерізі [math]z+p/\rho g=const[/math], а інтеграл
[math]\int\limits_{\infty }{ud\omega =v\omega }[/math]
отже, попередній вираз можна записати так:
[math]En=\rho g\frac{\left( z+\frac{p}{\rho g} \right)\int\limits_{\infty }{ud\omega }}{pg\int\limits_{\infty }{ud\omega }}+\frac{\int\limits_{\infty }{\frac{{{u}^{2}}}{2g}d\omega }}{v\omega }=z+\frac{p}{\rho g}+\frac{\int\limits_{\infty }{\frac{{{u}^{2}}}{2g}dw}}{vw}[/math]
Помноживши і розділивши останній члеи на [math]{{v}^{2}}[/math], одержимо
[math]En=z+\frac{p}{\rho g}+\frac{\alpha {{v}^{2}}}{2g}[/math]
де [math]\alpha =\frac{\int\limits_{\infty }{{{u}^{2}}d\omega }}{{{v}^{3}}\omega }[/math] - коефіцієнт кінетичної енергії (коефіцієнт Коріоліса)),який показує, у скільки разів дійсна кінетична енергія більша від обчисленої за середньою швидкістю.Значення коефіцієнта [math]\alpha[/math] залежить від ступеня нерівномірності розподілу швидкостей по живому перерізу і для різних епюр швидкостєй має різні значення, які завжди більші за одиницю.
Кінцевий вигляд рівняння
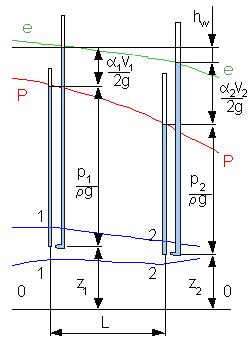
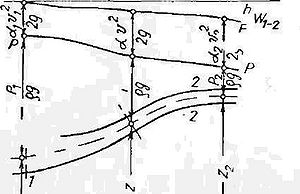
З урахуванням наведеного рівняння балансу питомої енергії для стаціонарного руху реальної рідини для перерізів 1—1 і 2—2 (рис.2) можна записати у вигляді[math]{{z}_{1}}+\frac{{{p}_{1}}}{\rho g}+\frac{{{\alpha }_{1}}{{v}^{2}}_{1}}{2g}={{z}_{2}}+\frac{{{p}_{2}}}{\rho g}+\frac{{{\alpha }_{2}}{{v}^{2}}_{2}}{2g}+{{h}_{W1-2}}[/math]
де [math]{{v}_{1}}[/math] , [math]{{v}_{2}}[/math] - середні швидкості руху рідини;
[math]\alpha[/math] - коефіцієнт кінетичної енергії, величина якого для турбулентних потоків як в трубах, так і у відкритих руслах 1 ≤ α ≤ 1,1.
[math]{{h}_{W1-2}}[/math] - питома енергія рідини, витрачена на подолання сил опору руху потоку на ділянці між перерізами (втрати енергії). Рівняння балансу питомої енергії назирають рівнянням Бернуллі для потоки в'язкої рідини
Література
- Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с.
- О.М. Коваленко,Т.О. Шевченко Інженерна гідравліка. Розділ I. Рух рідини в закритих руслах – Харків: ХНАМГ, 2007.-76 с.
- http://jpegator.com/gidrot5r2part1.html