Відмінності між версіями «Статистичні гіпотези і надійна імовірність»
Fenomix (обговорення • внесок) |
Fenomix (обговорення • внесок) |
||
| Рядок 36: | Рядок 36: | ||
# Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези. | # Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези. | ||
# Розрахунок статистики ϕ критерію такий, що: | # Розрахунок статистики ϕ критерію такий, що: | ||
| − | + | ## її величина залежить від початкової вибірки <math>X=(X_{1},...,X_{n}):f=f(X_{1},...,X_{n})</math>; | |
| − | + | ## за її значенням можна зробити висновки про істинність гіпотези H0; | |
| − | + | ## сама статистика f повинна підкорятися якомусь невідомому закону розподілу, так як сама f є випадковою в силу випадковості. | |
| − | # Побудова критичної області. З області значень | + | # Побудова критичної області. З області значень f виділяємо підмножину таких значень, за якими можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність<math>P(f\in\mathbb C )=\alpha</math>. Ця множина і називається критичною областю. |
| − | # Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику | + | # Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику f і за попаданням (або непопаданням) у критичну область виноситься ухвала про відкидання (або ухвалення) висунутої гіпотези H0. |
| + | == Класифікація статистичних гіпотез == | ||
| + | * Спрямовані гіпотези, висувають, якщо значення показника в одній сукупності вище (нижче), ніж в іншій; якщо під впливом якихось дій в одній сукупності відбуваються більш (менш) виражені зміни, ніж в іншій. | ||
| + | * Неспрямовані гіпотези формулюють, якщо необхідно довести лише відмінності форми або значень показників розподілу ознак. | ||
| + | * Параметричними називають гіпотези щодо невідомого значення параметра розподілу, що входить у деяке параметричне сімейство розподілів, наприклад, нормальних. | ||
| + | * Непараметричною гіпотезою називається припущення, при якому вид розподілу невідомий (тобто не передбачається, що воно входить у деяке параметричне сімейство розподілів). | ||
| + | == Надійна ймовірність == | ||
| + | Розглянемо тлумачення поняття рівень значущості. Імовірність відхилити вірну гіпотезу носить назву рівня значущості, оскільки це нижня межа імовірності, за якою лежать статистично незначущі її значення. Наприклад, імовірність, меншу ніж 0.05, називають незначущою. Якщо в п'яти або менше випадках із ста наш висновок не підтвердився і цією помилкою ми знехтуємо, вона не матиме значення. Якщо такий процент помилки нас не влаштовує і вважається занадто великим, слід прийняти вищий, наприклад 1%-й, рівень значущості. Таким чином, рівень значущості при переході від 0.05 до 0,01 зростає, результат порівняння показників стає більш значущим, надійним. Отже, рівень значущості, наприклад 0,05, ділить діапазон імовірності на дві частини: до однієї входять імовірності значущі, і ми ними не нехтуємо (від 1 до 0,05); до іншої — імовірності незначущі, які для даної задачі не беруться до уваги (від 0,05 до 0).<br> | ||
| + | |||
| + | У практичних обчисленнях заздалегідь задаються максимально припустимою помилкою <math>\alpha</math> або пов'язаною з нею імовірністю <math>y = 1 - \alpha</math>. Тоді ця імовірність стає надійною, вказує на ступінь надійності здобутого результату і функціонально пов'язана з надійним інтервалом аналізованої статистичної характеристики (наприклад, чим більша мішень, тим більша імовірність того, що в неї влучимо). Надійність результату або надійну імовірність можна розглядати як найменшу імовірність того, що результат є вірним.<br> | ||
| + | |||
| + | Припустимий процент можливих помилок, який відповідає деякому рівню значущості, вибирається дослідником або практиком у кожному конкретному випадку. Ця величина не може бути обчислена аналітично, проте на основі багаторічного досвіду встановлено різні значення надійної імовірності та пов'язані з нею рівні значущості, використовувані на практиці. Останні виражають імовірність, якою вирішено знехтувати (тобто імовірність помилкового результату) у даній області досліджень.<br> | ||
| + | |||
| + | Найчастіше надійна імовірність <math>y</math>=0,95, а відповідний рівень значущості <math>\alpha</math>=0,05. Рідше використовується більш висока надійна імовірність, що має значення <math>y</math> = 0.99 (<math>\alpha</math> - 0,01).<br> | ||
| + | |||
| + | Збільшення надійної ймовірності викликає зростання надійного інтервалу і підвищує надійність результатів аналізу експериментальних даних. Більша надійна імовірність дає змогу з більшою довірою ставитись до висновку в тому сенсі, що ми не відхилили вірну гіпотезу, її можна порівняти з позицією людей, які все бачать у рожевому світлі.<br> | ||
| + | |||
| + | Наприклад, вважаючи всіх людей добрими, вони не припустяться помилки першого роду і не назвуть добру людину поганою. При цьому вони мають досить шансів вважати доброю також і погану людину, тобто припуститися помилки другого роду. У цьому прикладі нульова гіпотеза формулюється так: кожна людина добра.<br> | ||
| + | |||
| + | Підсумовуючи сказане, можна підтвердити справедливість відомого у статистиці положення надійне висловлювання некатегоричне, категоричне висловлювання ненадійне. | ||
Версія за 01:52, 13 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| {{{img}}} | ||
| Імя | Павло | |
| Прізвище | Вашенюк | |
| По-батькові | Степанович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-11-205 | |
Гіпотеза — наукове припущення, що висувається для пояснення будь-якого явища і потребує перевірки на досліді та теоретичного обґрунтування, для того щоб стати достовірною науковою теорією. Також - недоведене твердження або здогад. Будь-яка гіпотеза повинна бути спростовуваною хоча б у принципі. Незаперечні припущення (наприклад, аксіоми) гіпотезами не є.
Особливістю гіпотези, як форми наукового знання є те, що вона завжди має певний ступінь імовірності, відмінний від 100%.
Статистичною гіпотезою називається будь-яке припущення щодо виду або параметрів невідомого закону розподілу. У конкретній ситуації статистичну гіпотезу формулюють як припущення на певному рівні статистичної значущості про властивості генеральної сукупності за оцінками вибірки.
Зміст
[сховати]Нульова та альтернативна гіпотези
При порівнянні статистичних характеристик висуваються припущення — гіпотези, наприклад про вид розподілу, належність вибіркових даних до однієї генеральної сукупності, рівність середнього арифметичного заданому значенню тощо. Гіпотези позначають літерою Н (Hypo-thesis — припущення).
Висовувану статистичну гіпотезу називають нульовою (нуль-гіпотезою) і позначають Н0. Часто для стислості нуль-гіпотезу формулюють так: відмінностей немає, а ті, що спостерігаються, випадкові.
Протилежну гіпотезу, тобто припущення про те, що відмінності не випадкові називають альтернативною і позначають Нa. У загальному випадку альтернативних гіпотез може бути декілька.
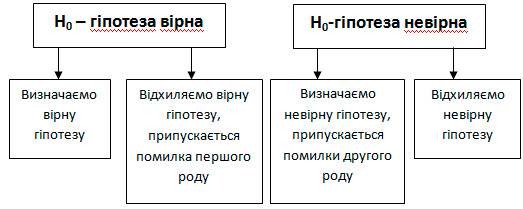
Рішення про відхилення чи визнання статистичної гіпотези проводять на основі дослідних даних, які супроводжуються випадковими помилками. Тому не виключена можливість помилки також при прийнятті рішення, причому можливі два варіант помилкових рішень:
- може бути відхилена, у дійсності вірна, нуль-гіпотеза — це помилка першого роду;
- може бути визнана, у дійсності невірна, нуль-гіпотеза — це помилка другого роду.
Отже, два варіанти помилкових рішень виникають відповідно до висунутої нуль-гіпотези, як вірної, так і невірної. Не відхилена гіпотеза (вірна чи невірна) визнається, і таким чином можливі чотири наслідки при прийнятті рішення.
Прикладами формулювання нульової та альтернативної гіпотез є:
- Н0: Розподіл даної вибірки є нормальним. Нa: Розподіл даної вибірки відрізняється від нормального
- Н0: Середня ефективність даного препарату дорівнює нулю.Нa: Середня ефективність даного препарату відрізняється від нуля (це строге формулювання альтернативної гіпотези, зазвичай її розуміють як твердження про ефективність препарату)
- Н0: Зв'язок між ознаками вибірки відсутній. Нa: Існує зв'язок між ознаками вибірки
Перевірка статистичних гіпотез
Необхідність перевірки статистичних гіпотез виникає у різних сферах економічної і соціальної діяльності людей. Оцінювання певної ознаки генеральної сукупності здійснюється на основі цієї ж ознаки в вибірковій сукупності із врахуванням помилки репрезентативності. А по відношенню властивостей генеральної сукупності висувається деяка гіпотеза про величину середньої, дисперсії, характер розподілу, форму і тісноту зв'язку між досліджуваними змінними. Перевірку гіпотези проводять на основі виявлення узгодження фактичних і теоретичних даних. Якщо розбіжності між порівнюваними даними знаходяться в межах випадкових помилок, гіпотезу приймають.
Основні етапи перевірки:
- Формулювання основної гіпотези H0 і конкуруючої гіпотези H1. Гіпотези повинні бути чітко формалізовані в математичних термінах.
- Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези.
- Розрахунок статистики ϕ критерію такий, що:
- її величина залежить від початкової вибірки [math]X=(X_{1},...,X_{n}):f=f(X_{1},...,X_{n})[/math];
- за її значенням можна зробити висновки про істинність гіпотези H0;
- сама статистика f повинна підкорятися якомусь невідомому закону розподілу, так як сама f є випадковою в силу випадковості.
- Побудова критичної області. З області значень f виділяємо підмножину таких значень, за якими можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність[math]P(f\in\mathbb C )=\alpha[/math]. Ця множина і називається критичною областю.
- Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику f і за попаданням (або непопаданням) у критичну область виноситься ухвала про відкидання (або ухвалення) висунутої гіпотези H0.
Класифікація статистичних гіпотез
- Спрямовані гіпотези, висувають, якщо значення показника в одній сукупності вище (нижче), ніж в іншій; якщо під впливом якихось дій в одній сукупності відбуваються більш (менш) виражені зміни, ніж в іншій.
- Неспрямовані гіпотези формулюють, якщо необхідно довести лише відмінності форми або значень показників розподілу ознак.
- Параметричними називають гіпотези щодо невідомого значення параметра розподілу, що входить у деяке параметричне сімейство розподілів, наприклад, нормальних.
- Непараметричною гіпотезою називається припущення, при якому вид розподілу невідомий (тобто не передбачається, що воно входить у деяке параметричне сімейство розподілів).
Надійна ймовірність
Розглянемо тлумачення поняття рівень значущості. Імовірність відхилити вірну гіпотезу носить назву рівня значущості, оскільки це нижня межа імовірності, за якою лежать статистично незначущі її значення. Наприклад, імовірність, меншу ніж 0.05, називають незначущою. Якщо в п'яти або менше випадках із ста наш висновок не підтвердився і цією помилкою ми знехтуємо, вона не матиме значення. Якщо такий процент помилки нас не влаштовує і вважається занадто великим, слід прийняти вищий, наприклад 1%-й, рівень значущості. Таким чином, рівень значущості при переході від 0.05 до 0,01 зростає, результат порівняння показників стає більш значущим, надійним. Отже, рівень значущості, наприклад 0,05, ділить діапазон імовірності на дві частини: до однієї входять імовірності значущі, і ми ними не нехтуємо (від 1 до 0,05); до іншої — імовірності незначущі, які для даної задачі не беруться до уваги (від 0,05 до 0).
У практичних обчисленнях заздалегідь задаються максимально припустимою помилкою [math]\alpha[/math] або пов'язаною з нею імовірністю [math]y = 1 - \alpha[/math]. Тоді ця імовірність стає надійною, вказує на ступінь надійності здобутого результату і функціонально пов'язана з надійним інтервалом аналізованої статистичної характеристики (наприклад, чим більша мішень, тим більша імовірність того, що в неї влучимо). Надійність результату або надійну імовірність можна розглядати як найменшу імовірність того, що результат є вірним.
Припустимий процент можливих помилок, який відповідає деякому рівню значущості, вибирається дослідником або практиком у кожному конкретному випадку. Ця величина не може бути обчислена аналітично, проте на основі багаторічного досвіду встановлено різні значення надійної імовірності та пов'язані з нею рівні значущості, використовувані на практиці. Останні виражають імовірність, якою вирішено знехтувати (тобто імовірність помилкового результату) у даній області досліджень.
Найчастіше надійна імовірність [math]y[/math]=0,95, а відповідний рівень значущості [math]\alpha[/math]=0,05. Рідше використовується більш висока надійна імовірність, що має значення [math]y[/math] = 0.99 ([math]\alpha[/math] - 0,01).
Збільшення надійної ймовірності викликає зростання надійного інтервалу і підвищує надійність результатів аналізу експериментальних даних. Більша надійна імовірність дає змогу з більшою довірою ставитись до висновку в тому сенсі, що ми не відхилили вірну гіпотезу, її можна порівняти з позицією людей, які все бачать у рожевому світлі.
Наприклад, вважаючи всіх людей добрими, вони не припустяться помилки першого роду і не назвуть добру людину поганою. При цьому вони мають досить шансів вважати доброю також і погану людину, тобто припуститися помилки другого роду. У цьому прикладі нульова гіпотеза формулюється так: кожна людина добра.
Підсумовуючи сказане, можна підтвердити справедливість відомого у статистиці положення надійне висловлювання некатегоричне, категоричне висловлювання ненадійне.