Відмінності між версіями «Ядерне згладжуваня»
Vova (обговорення • внесок) (→Последовательность весов) |
Vova (обговорення • внесок) (→Приклад функції ядра) |
||
| (Не показано 25 проміжних версій цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | ''' | + | {{Завдання|Шостак В.М.|Назаревич О. Б.|18 березня 2012}} |
| + | {{Студент | Name=Володимир | Surname=Шостак | FatherNAme=Михайлович |Faculti=ФІС | Group=СН-51 | Zalbook=СН-11-222}} | ||
| + | '''Ядерне згладжуваня''' - один із найпростіших видів [[Непараметрична регресія|непараметричної регресії]]. | ||
| − | == Постановка | + | == Постановка задачі == |
| − | : | + | :Вирішується завдання відновлення регресії. Заданий простір об'єктів <math>x</math> і безліч можливих відповідей <math>y=r</math>. Існує невідома цільова залежність <math> y^*: X \rightarrow Y</math>, значення якої відомі лише на об'єктах навчальної вибірки <math> X^m={(x_i, y_i)}_{i=1}^m</math>. Потрібно побудувати алгоритм <math>a: X \rightarrow Y </math>, що апроксимує цільову залежність <math>y^*</math>. |
| − | |||
| − | |||
| − | |||
== Принцип == | == Принцип == | ||
| − | Принцип, | + | Принцип, використання ідейно простого підхіду до уявлення послідовності вагів <math>\{ W_{mi}(x)\}_{i=1}^m</math> полягає в описі форми вагової функції <math>w_{mi}(x) </math> за допомогою функції щільності із скалярним параметром, який регулює розмір і форму вагів біля х. Цю функцію форми прийнято називати ''''ядром'''' <math>k</math>. |
| − | + | Отримані таким чином ваги далі використовуються для представлення величини <math>a(x) </math> у вигляді зваженої суми значень <math>y_i</math> навчаючої вибірки. | |
| − | |||
| − | + | == Опис методу == | |
| − | + | === Визначення ядра === | |
| − | == | + | '''Ядро''' — це неперермвна обмеженна симетрична речовина функція <math>K</math> з одиничним інтегралом |
| − | === | ||
| − | '''Ядро''' — | ||
::<math>\int K(u)du=1</math> | ::<math>\int K(u)du=1</math> | ||
| − | === | + | === Послідовність ваги === |
| − | + | Послідовність ваги для ядерних оцінок (для одновимірного <math>x</math>) знаходиться як ::<math>W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}</math>, | |
| − | + | де | |
::<math>\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)</math>, | ::<math>\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)</math>, | ||
a | a | ||
::<math>K_{h_m}(u)=\frac{1}{h_m} K\(\frac{u}{h_m}\)</math> | ::<math>K_{h_m}(u)=\frac{1}{h_m} K\(\frac{u}{h_m}\)</math> | ||
| − | + | уявимо собі ядро з параметром <math>h_m</math>. Також цей параметр прийнято називати шириной вікна. Підкреслемо залежність <math>h\ =\ h_m</math> від об'єму вибірки <math>m</math>, умова скороченого значення послідовністі ваги <math>W_{mi}(x)</math>. | |
| − | === | + | === Функція ядра === |
| − | + | Функція <math>\hat{f}_{h_m}(x)</math> являєтся ''ядерною оцінкою щільності Розенблата — Парзена'' (Rosenblatt, 1956; Parzen, 1962) для (маргинальної) щільності зміної <math>x</math>. Даний вид ядерних вагів <math>W_{mi}(x)</math> був запропонований в работах (Nadaraya, 1964) і (Watson, 1964). Як наслідок, оцінка очікуваної величини відновлюваної залежності <math>e(y\|x) </math>: ::<math>\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i) Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i)}</math> | |
| − | + | часто називають оцінкою ''Надарая—Ватсона''. | |
| − | + | Ширіна вікна визначає, наскільки швидко убувають ваги <math>w_{mi}(x) </math> у міру видалення об'єктів <math>x_i</math> від <math>x</math>. | |
| − | ::< | ||
| − | часто | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | Характер убування визначається виглядом ядра <math>k</math>. |
| + | Нормалізація вагів <math>\hat{f}_{h_m}(x)</math> гарантує, що сума вагів дорівнює одиниці. | ||
| + | |||
| + | '''Примітка'''. При ряду умов має місце збіжність по вірогідності даної оцінки до <math>e(y|x) </math>. | ||
| − | === | + | === Приклад функції ядра === |
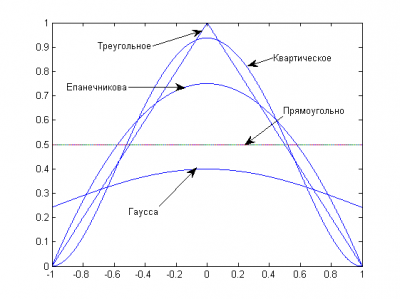
| − | [[ | + | [[Файл:CoreFunc.png|thumb|right|400px|Приклади різних функцій ядра.]] |
| − | На | + | На практиці використовується декілька видів ядерних функцій. |
Чаще всего используется квартическая ядерная функция | Чаще всего используется квартическая ядерная функция | ||
| − | ::< | + | ::<math>K(u)=(15/16)(1-u^2)^2I(\| u \| \le 1)</math>. |
| − | + | Також викоритовуєтьсятся ядро Епанечникова, яке володіє деякими властивостями оптимальності [Хардле В п 4.5]; це функція | |
параболического типа (Epanechnikov, 1969; Bartlett, 1963): | параболического типа (Epanechnikov, 1969; Bartlett, 1963): | ||
| − | ::< | + | ::<math>K(u)=0.75(1-u^2)I(\| u \| \le 1)</math>. |
| − | + | Іншим прикладом є ядро Гаусса, | |
| − | ::< | + | ::<math>K(u)=(2\pi)^{-1/2} \exp(-u^2/2)</math>, |
| − | + | трикутне ядро | |
| − | ::< | + | ::<math>K(u)=(1-\|u\|)I(\| u \| \le 1)</math>, |
| − | + | і прямокутне ядро | |
| − | ::< | + | ::<math>K(u)=(1/2)I(\| u \| \le 1)</math>. |
| − | ''' | + | '''Примітка'''. Точність відновленоії залежності мало залежить від вибору ядра. |
| − | Ядро | + | Ядро визначає міру гладкості функції <math>a(x)</math>. |
| − | === | + | === Залежність від ширини вікна === |
| − | + | Вибір вікна вирішальним чином впливає на точність відновлюваної залежності. При занадто малих значеннях <math>h</math> крива <math>a(x) </math> прагне пройти через кожну точку вибірки, гостро реагуючи на шуми і зазнаючи різкі скачки, оскільки в цьому випадку оцінка опирається лише на невелике число спостережень з вузької окружності точки <math>x</math>. Навпаки, якщо ширина вікна велика, функція надмірно згладжується і в межі при <math> h \rightarrow \infty</math> вироджується в константу -- усереднене значення величин <math> y_i</math>. В цьому випадку згладжена функція не дає можливості визначити характерні особливості шуканої залежності <math> y^*(x) </math>. | |
| − | При | ||
| − | скачки, | ||
| − | |||
| − | |||
| − | == | + | ==Література== |
| − | # | + | # ''Хардле В.''[http://optimization.nlprog.ru/read/ru/8776859F6322A5AF21D45220A9B5B57E110C2E84/index.htm/ Прикладна непараметрична регресія]-1989р. |
| − | + | # ''Воронцов К.В.''[http://www.ccas.ru/voron/download/Regression.pdf/ Лекції по алгоритмам відновлення регресії] - 2007. | |
| − | + | # ''Лагутин М.Б.''Прикладна математична статистика.- 2009 | |
| − | + | ||
| − | + | ==Див. також== | |
| − | |||
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
* [[Алгоритм LOWESS]] | * [[Алгоритм LOWESS]] | ||
| − | * [[ | + | * [[Варіація і зміщення]] |
| − | * [[ | + | * [[Регресійний аналіз]] |
| − | |||
| − | |||
| − | + | ==посилання== | |
| + | [[Непараметрична регресія]] | ||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 19:31, 13 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| {{{img}}} | ||
| Імя | Володимир | |
| Прізвище | Шостак | |
| По-батькові | Михайлович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-11-222 | |
Ядерне згладжуваня - один із найпростіших видів непараметричної регресії.
Зміст
Постановка задачі
- Вирішується завдання відновлення регресії. Заданий простір об'єктів [math]x[/math] і безліч можливих відповідей [math]y=r[/math]. Існує невідома цільова залежність [math]y^*: X \rightarrow Y[/math], значення якої відомі лише на об'єктах навчальної вибірки [math]X^m={(x_i, y_i)}_{i=1}^m[/math]. Потрібно побудувати алгоритм [math]a: X \rightarrow Y[/math], що апроксимує цільову залежність [math]y^*[/math].
Принцип
Принцип, використання ідейно простого підхіду до уявлення послідовності вагів [math]\{ W_{mi}(x)\}_{i=1}^m[/math] полягає в описі форми вагової функції [math]w_{mi}(x)[/math] за допомогою функції щільності із скалярним параметром, який регулює розмір і форму вагів біля х. Цю функцію форми прийнято називати 'ядром' [math]k[/math]. Отримані таким чином ваги далі використовуються для представлення величини [math]a(x)[/math] у вигляді зваженої суми значень [math]y_i[/math] навчаючої вибірки.
Опис методу
Визначення ядра
Ядро — це неперермвна обмеженна симетрична речовина функція [math]K[/math] з одиничним інтегралом
- [math]\int K(u)du=1[/math]
Послідовність ваги
Послідовність ваги для ядерних оцінок (для одновимірного [math]x[/math]) знаходиться як ::[math]W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}[/math], де
- [math]\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)[/math],
a
- [math]K_{h_m}(u)=\frac{1}{h_m} K\(\frac{u}{h_m}\)[/math]
уявимо собі ядро з параметром [math]h_m[/math]. Також цей параметр прийнято називати шириной вікна. Підкреслемо залежність [math]h\ =\ h_m[/math] від об'єму вибірки [math]m[/math], умова скороченого значення послідовністі ваги [math]W_{mi}(x)[/math].
Функція ядра
Функція [math]\hat{f}_{h_m}(x)[/math] являєтся ядерною оцінкою щільності Розенблата — Парзена (Rosenblatt, 1956; Parzen, 1962) для (маргинальної) щільності зміної [math]x[/math]. Даний вид ядерних вагів [math]W_{mi}(x)[/math] був запропонований в работах (Nadaraya, 1964) і (Watson, 1964). Як наслідок, оцінка очікуваної величини відновлюваної залежності [math]e(y\|x)[/math]: ::[math]\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i) Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-x_i)}[/math] часто називають оцінкою Надарая—Ватсона. Ширіна вікна визначає, наскільки швидко убувають ваги [math]w_{mi}(x)[/math] у міру видалення об'єктів [math]x_i[/math] від [math]x[/math].
Характер убування визначається виглядом ядра [math]k[/math]. Нормалізація вагів [math]\hat{f}_{h_m}(x)[/math] гарантує, що сума вагів дорівнює одиниці.
Примітка. При ряду умов має місце збіжність по вірогідності даної оцінки до [math]e(y|x)[/math].
Приклад функції ядра
На практиці використовується декілька видів ядерних функцій. Чаще всего используется квартическая ядерная функция
- [math]K(u)=(15/16)(1-u^2)^2I(\| u \| \le 1)[/math].
Також викоритовуєтьсятся ядро Епанечникова, яке володіє деякими властивостями оптимальності [Хардле В п 4.5]; це функція параболического типа (Epanechnikov, 1969; Bartlett, 1963):
- [math]K(u)=0.75(1-u^2)I(\| u \| \le 1)[/math].
Іншим прикладом є ядро Гаусса,
- [math]K(u)=(2\pi)^{-1/2} \exp(-u^2/2)[/math],
трикутне ядро
- [math]K(u)=(1-\|u\|)I(\| u \| \le 1)[/math],
і прямокутне ядро
- [math]K(u)=(1/2)I(\| u \| \le 1)[/math].
Примітка. Точність відновленоії залежності мало залежить від вибору ядра. Ядро визначає міру гладкості функції [math]a(x)[/math].
Залежність від ширини вікна
Вибір вікна вирішальним чином впливає на точність відновлюваної залежності. При занадто малих значеннях [math]h[/math] крива [math]a(x)[/math] прагне пройти через кожну точку вибірки, гостро реагуючи на шуми і зазнаючи різкі скачки, оскільки в цьому випадку оцінка опирається лише на невелике число спостережень з вузької окружності точки [math]x[/math]. Навпаки, якщо ширина вікна велика, функція надмірно згладжується і в межі при [math]h \rightarrow \infty[/math] вироджується в константу -- усереднене значення величин [math]y_i[/math]. В цьому випадку згладжена функція не дає можливості визначити характерні особливості шуканої залежності [math]y^*(x)[/math].
Література
- Хардле В.Прикладна непараметрична регресія-1989р.
- Воронцов К.В.Лекції по алгоритмам відновлення регресії - 2007.
- Лагутин М.Б.Прикладна математична статистика.- 2009