Відмінності між версіями «Попередня обробка експериментальних даних»
| Рядок 19: | Рядок 19: | ||
Метод найменших квадратів запропонував К. Гаус (1794—95) і А. Лежандром (1805—06). Строге математичне обґрунтовування методу було дано А. А. Марковим (старшим) і А. Н. Колмогоровим. Нині цей метод є одним з найважливіших розділів математичної статистики і широко використовується для статистичних висновків в різних областях науки і техніки. | Метод найменших квадратів запропонував К. Гаус (1794—95) і А. Лежандром (1805—06). Строге математичне обґрунтовування методу було дано А. А. Марковим (старшим) і А. Н. Колмогоровим. Нині цей метод є одним з найважливіших розділів математичної статистики і широко використовується для статистичних висновків в різних областях науки і техніки. | ||
<br> | <br> | ||
| − | Суть методу найменших квадратів (по Гаусу) полягає в припущені, що «збиток» від заміни точного (невідомого) значення фізичної величини m її наближеним значенням X, обчисленим за наслідками спостережень, пропорційний квадрату помилки: | + | Суть методу найменших квадратів (по Гаусу) полягає в припущені, що «збиток» від заміни точного (невідомого) значення фізичної величини m її наближеним значенням X, обчисленим за наслідками спостережень, пропорційний квадрату помилки:<math>{{(X-m)}^{2}}</math>.Оптимальною оцінкою визнають величину X , позбавлену систематичної помилки, для якої середнє значення «збитку» мінімальне. |
| − | Оптимальною оцінкою визнають величину X , позбавлену систематичної помилки, для якої середнє значення «збитку» мінімальне. | ||
Задачу пошуку оптимальної оцінки звужують і як Х вибирають лінійну функцію від результатів спостережень, позбавлену систематичної помилки, і таку, для якої середнє значення «збитку» мінімальне в класі всіх лінійних функцій. Якщо випадкові помилки спостережень мають нормальний розподіл і оцінювана величина m залежить від середніх значень результатів спостережень лінійно, то рішення цієї задачі одночасно буде і рішенням загальної задачі. Оцінка X, обчислена згідно методу найменших квадратів — найвірогідніше значення невідомого параметра m. | Задачу пошуку оптимальної оцінки звужують і як Х вибирають лінійну функцію від результатів спостережень, позбавлену систематичної помилки, і таку, для якої середнє значення «збитку» мінімальне в класі всіх лінійних функцій. Якщо випадкові помилки спостережень мають нормальний розподіл і оцінювана величина m залежить від середніх значень результатів спостережень лінійно, то рішення цієї задачі одночасно буде і рішенням загальної задачі. Оцінка X, обчислена згідно методу найменших квадратів — найвірогідніше значення невідомого параметра m. | ||
<br> | <br> | ||
| Рядок 50: | Рядок 49: | ||
Результати згладжування експериментальних даних зображено на рисунку: | Результати згладжування експериментальних даних зображено на рисунку: | ||
<br> | <br> | ||
| − | [[Файл:n-1.JPEG| | + | [[Файл:n-1.JPEG|650x180px|border|center|Результати згладжування експериментальних даних]] |
<br> | <br> | ||
Версія за 18:18, 27 лютого 2010
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
Зміст
Попередня обробка експериментальних даних. Критерії відсіювання завідомо помилкових даних
http://elartu.tstu.edu.ua/handle/123456789/380 Презентація доповіді (університетський репозиторій).
Зміст та завдання попередньої обробки експериментальних даних
Результати вимірювань – це випадкові величини, тобто в ході експерименту інформація спотворена перешкодами, і за одних і тих же умов можна отримати різні дані.
Зміст попередньої обробки даних полягає у відсіюванні грубих похибок і оцінці достовірності результатів вимірювань. Попередня обробка результатів вимірювань необхідна для того, щоб надалі, при побудові функцій відгуку, з найбільшою ефективністю використовувати статистичні методи і коректно аналізувати отримані результати.
Завданням попередньої обробки даних є перевірка відповідності результатів вимірювання нормальному закону і визначення параметрів цього розподілу. Якщо відгук суперечить нормальному розподілу, то слід визначити, якому закону розподілу підлягають дослідні дані або, якщо це можливо, перетворити досліджуваний розподіл до нормального вигляду.
Методи обробки експериментальних даних
Метод найменших квадратів
Для обробки експериментальних даних найчастіше на практиці використовують метод найменших квадратів - один з методів теорії помилок, що використовується для оцінки невідомих величин за наслідками вимірювань, що містить випадкові помилки (спричиняються різного роду випадковими причинами, які діють при кожному з окремих вимірювань непередбаченим чином).
Метод найменших квадратів запропонував К. Гаус (1794—95) і А. Лежандром (1805—06). Строге математичне обґрунтовування методу було дано А. А. Марковим (старшим) і А. Н. Колмогоровим. Нині цей метод є одним з найважливіших розділів математичної статистики і широко використовується для статистичних висновків в різних областях науки і техніки.
Суть методу найменших квадратів (по Гаусу) полягає в припущені, що «збиток» від заміни точного (невідомого) значення фізичної величини m її наближеним значенням X, обчисленим за наслідками спостережень, пропорційний квадрату помилки:[math]{{(X-m)}^{2}}[/math].Оптимальною оцінкою визнають величину X , позбавлену систематичної помилки, для якої середнє значення «збитку» мінімальне.
Задачу пошуку оптимальної оцінки звужують і як Х вибирають лінійну функцію від результатів спостережень, позбавлену систематичної помилки, і таку, для якої середнє значення «збитку» мінімальне в класі всіх лінійних функцій. Якщо випадкові помилки спостережень мають нормальний розподіл і оцінювана величина m залежить від середніх значень результатів спостережень лінійно, то рішення цієї задачі одночасно буде і рішенням загальної задачі. Оцінка X, обчислена згідно методу найменших квадратів — найвірогідніше значення невідомого параметра m.
Метод найменших квадратів дає найбільш бажаний результат тоді, коли випадкова помилка має порівняно невелику величину. В іншому разі необхідним є проведення попередньої обробки експериментальних даних, яка полягає в наступному: вихідні записи випадкових величин згладжуються певним способом, що дає змогу виявити основну тенденцію у їхній зміні.
Метод виключення перешкод
Метод виключення перешкод полягає у проведенні на око середньої лінії, яка враховує тільки основні коливання змінної. Інформація, що надалі буде зніматись із цієї середньої лінії, при математичній обробці даних буде використовуватись як вихідна.
Значення випадкової величини, що не збігаються із середньою лінією, прямо не впливатимуть на подальші висновки.
Метод оновлюваної середньої
Метод оновлюваної середньої полягає у використанні рекурентної формули для обчислення середнього арифметичного . Якщо випадкова величина х надходить у вигляді дискретних вимірів і для (N - 1) - го виміру обчислено середнє значення , то поява нового виміру змінює попереднє середнє значення на величину
При згладжуванні цим методом у кожній точці на часовій осі виміряне значення замінюється на середнє, розраховане на даний момент часу.
Послідовність обчислених за рекурентною формулою середніх значень є позбавленим від перешкод рядом вимірів змінної х, який використовується при подальшій обробці.
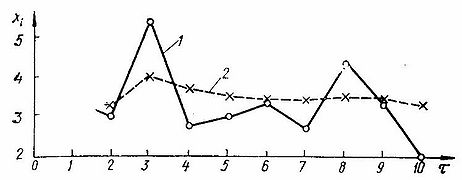
Розглянемо згладжування методом оновлюваної середньої наступного ряду вимірювань величини х:
Перше значення збігається з х1. Друге значення обчислюється за рекурентною формулою:
Отже:[math]{{\bar{x}}_{2}}=3.4+\frac{1}{2}(3.1-3.4)=3.25[/math];[math]{{\bar{x}}_{3}}=3.25+\frac{1}{3}(5.4-3.25)=3.96[/math];
[math]{{\bar{x}}_{4}}=3.65[/math];[math]{{\bar{x}}_{5}}=3.50[/math];[math]{{\bar{x}}_{6}}=3.46[/math];[math]{{\bar{x}}_{7}}=3.35[/math];[math]{{\bar{x}}_{8}}=3.47[/math];[math]{{\bar{x}}_{9}}=3.44[/math];[math]{{\bar{x}}_{10}}=3.30[/math].
Результати згладжування експериментальних даних зображено на рисунку:
Метод ковзної середньої
Метод ковзної середньої полягає в послідовному усередненні на деякому інтервалі [math]{{\tau }_{y}}[/math] значень вимірюваної величини х. Рухаючи [math]{{\tau }_{y}}[/math] уздовж осі часу для всіх точок [math]{{\tau }_{i}}[/math], що попали в нього, відповідні значення [math]{{x}_{i}}[/math] замінимо середніми значеннями; віднесемо ці значення до середини відповідного інтервалу. Операція згладжування виконується за формулою:
де і – номер інтервалу; (l+1) – число вимірювань у і-тому інтервалі; [math](i+\frac{l}{2})[/math] - номер замінюваного вимірювання.
Якщо попередня оцінка виконана невдало і після згладжування залишаються перешкоди, утворені дані знову можна піддати усередненню і робити це багаторазово, до бажаного результату.
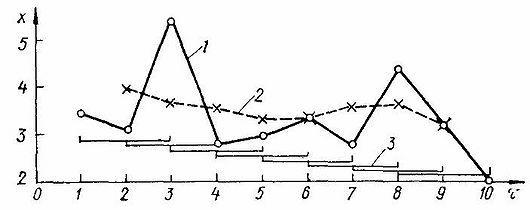
Для ряду вимірювань
обчислимо згладжені значення на інтервалі l+1=3,використовуючи формулу:
Отже, [math]{{\bar{x}}_{1+\frac{2}{2}}}={{\bar{x}}_{2}}=\frac{1}{3}(3.4+3.1+5.4)=3.97[/math]; [math]{{\bar{x}}_{2+\frac{2}{2}}}={{\bar{x}}_{3}}=\frac{1}{3}(3.1+5.4+2.7)=3.73[/math]; [math]{{\bar{x}}_{4}}=3.66[/math]; [math]{{\bar{x}}_{5}}=3.97[/math]; [math]{{\bar{x}}_{6}}=2.97[/math]; [math]{{\bar{x}}_{7}}=3.43[/math]; [math]{{\bar{x}}_{8}}=3.40[/math]; [math]{{\bar{x}}_{9}}=3.16[/math]
На рисунку наведено результат згладжування:
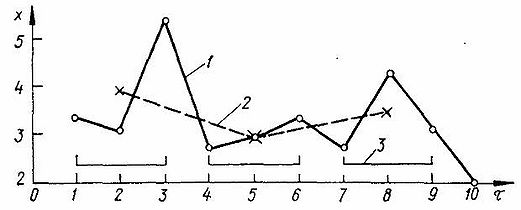
Іноді при згладжуванні заокруглюють наближення, використовуючи середні значення для не перекриваючих один одного інтервалів. Для цього обчислюють середнє значення за трьома першими точками, приписують результат середині інтервалу, а для наступного обчислення середньої використовують 4-ту, 5-ту і 6-ту точки і т. д.
В обох випадках частина початкової і кінцевої інформації втрачається.
Метод експоненційного згладжування
Цей метод має найширші можливості. Тут використовують наступні формули:
де [math]\alpha[/math] - параметр згладжування, який вибирається в діапазоні 0..1. Тут обчислювана середня заміняє відповідне значення вимірюваної змінної.
Від величини [math]\alpha[/math] залежать згладжуючи властивості методу. При різних [math]\alpha[/math] можна добувати з вихідної інформації високочастотні або низькочастотні складові. Таким чином, з’являється можливість боротися з низько – і високочастотними шумами, тобто зі швидко – і повільно змінними у часі перешкодами.
При малих , близьких до 0 [math]\alpha[/math], сукупність обчислених середніх відобразить низькочастотні зміни вимірюваної змінної, позбавивши їх швидкозмінних перешкод. У цьому випадку говорять про інерційне згладжування, при якому обчислювана середня мало залежить від останнього вимірювання і значною мірою від середньої, утвореної на попередньому кроці.
Якщо обрана величина [math]\alpha[/math] - близька до 1 (наприклад, становить 0,6), то згладжування буде мало інерційним, значення ближчими до вимірюваних значень х, тобто високі частоти зберігатимуться:
Критерії відсіювання завідомо помилкових даних
Дані, які відповідають умовам, що змінилися, називають грубими помилками або значеннями, що різко виділяються (аномальними). У разі відсіву грубих помилок формулюється нульова гіпотеза:
Альтернативною гіпотезою може бути:
Найпоширенішими і теоретично обґрунтованими в цьому випадку є
- критерій Н.В. Смірнова (використовується при [math]H_{1}^{(1)}[/math])
- і критерій Діксона (застосовується як при [math]H_{1}^{(1)}[/math] так і при [math]H_{1}^{(2)}[/math])
Критерій Н. В. Смірнова
Якщо відомо, що є тільки одне аномальне значення (альтернативна гіпотеза [math]H_{1}^{(1)}[/math]), то воно буде крайнім членом варіаційного ряду. Тому перевіряти вибірку на наявність однієї грубої помилки природно за допомогою статистики (якщо сумнів викликає перший член варіаційного ряду [math]{{x}_{1}}=\min {{x}_{i}}[/math]:
або якщо сумніви викликає максимальний член варіаційного ряду [math]{{x}_{n}}=\max {{x}_{i}}[/math]:
Цей критерій вперше був запропонований Н.В. Смірновим. Він досліджував розподіл цих статистик і склав таблиці процентних точок
[math]{{u}_{\alpha ,n}}[/math]. При вибраному рівні значущості критична область для критерію Н.В. Смірнова будується таким чином:
де [math]{{u}_{\alpha ,n}}[/math] – це табличні значення
У випадку якщо виконується остання умова (статистика потрапляє в критичну область), то нульова гіпотеза відхиляється, тобто викид х1 або хn не випадковий і не характерний для даної сукупності даних, а визначається умовами, що змінилися або грубими помилками при проведенні дослідів.
В цьому випадку значення або виключають з розгляду, а знайдені раніше оцінки піддаються коректуванню з урахуванням відкинутого результату.
Критерій Діксона
В критерії Діксона застосовується статистика:
- якщо підозріла «чужорідна» точка має найбільше значення:
- якщо підозріла «чужорідна» точка має найменше значення:
Де [math]{{x}_{n}},{{x}_{n-i}},{{x}_{j+1}}[/math] – члени варіаційного ряду [math]{{x}_{1}}\le {{x}_{2}}\le {{x}_{3}}...\le {{x}_{i}}...\le {{x}_{n}}[/math]
Діксоном були отримані розподіли для статистик [math]{{r}_{10}},{{r}_{11}},{{r}_{12}},{{r}_{20}},{{r}_{21}},{{r}_{22}}[/math] при об’ємі вибірки 3 <=n<=30.
Наприклад, статистика
використовується для перевірки максимального або мінімального члена варіаційного ряду (одна груба помилка, альтернативна гіпотеза [math]H_{1}^{(1)}[/math]) при 3 <= n <= 7.
Якщо при тому ж об'ємі вибірки передбачається наявність двох і більше значень, що різко виділяються (альтернативна гіпотеза [math]H_{1}^{(2)}[/math]), то використовується статистика [math]{{r}_{20}}[/math].
Статистики критерію Діксона, що використовуються при інших об'ємах вибірки, приведені в таблиці:
Перелік використаних джерел
- Большая Советская Энциклопедия // режим доступу: http://bse.sci-lib.com/article086042.html (станом на 13.02.10)
- Н. А. Спирин, В. В. Лавров. Методы планирования и обработки результатов инженерного эксперимента. – Екатеринбург: 2004, - 257 с.
- В. О. Аністратенко, В. Г. Федоров. Математичне планування експериментів в АПК. Київ: Вища школа, - 1993, - 375 с.