Відмінності між версіями «Гідростатичний тиск і його властивості»
м |
|||
| (Не показано одну проміжну версію цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
| − | [[Файл:Гідростатичний_тиск.JPG| | + | ==Поняття "гідростатичний тиск" == |
| + | [[Файл:Гідростатичний_тиск.JPG|200px|thumb|right|]] | ||
| + | '''Гідростатичний тиск''' <math>p</math> (рос.гидростатическое давление, англ. hydrostatic pressure, нім. Wasserdruckhöne) - | ||
| − | + | * це тиск рідини в будь-якій точці об'єму цієї рідини. Тиск у рідині, що перебуває у стані спокою, створений сумою тиску газу на її вільній поверхні і зумовленого силою тяжіння тиску стовпа рідини, розташованого над точкою вимірювання. Г. т. залежить від глибини занурення. | |
| + | |||
| + | * це напруга стиску в точці, розміщеній всередині рідини, що знаходиться в стані спокою: | ||
<math>\ p = \lim_{\Delta \omega\to\0}\frac{{\Delta \ P}}{{\Delta \omega}}</math>, | <math>\ p = \lim_{\Delta \omega\to\0}\frac{{\Delta \ P}}{{\Delta \omega}}</math>, | ||
| − | де <math>\Delta \ P</math> - сила тиску, що діє на елементарну площинку <math>\Delta \omega </math>, яка включає в | + | де <math>\Delta \ P</math> - сила тиску, що діє на елементарну площинку <math>\Delta \omega </math>, яка включає в собі дану точку. |
| + | |||
| + | В гідрогеології поняття гідростатичного тиску трактується ширше: гідростатичний тиск - це тиск рідини (рухомої або нерухомої) у певній точці водоносної системи. Тобто гідростатичний тиск — загальна величина трьох головних напружень в будь-якій точці гірничого масиву, що перебуває в стані спокою. Високий гідростатичний тиск сприяє обваленню порід покрівлі та підйому підошви виробки, де спостерігаються раптові прориви вод і пливунів. | ||
На зовнішній поверхні рідини гідростатичний тиск завжди спрямований по нормалі до площини, на яку він діє, а в будь-якій точці всередині рідини його величина не залежить від орієнтації площинки в просторі. Він є лише функцією координат. | На зовнішній поверхні рідини гідростатичний тиск завжди спрямований по нормалі до площини, на яку він діє, а в будь-якій точці всередині рідини його величина не залежить від орієнтації площинки в просторі. Він є лише функцією координат. | ||
| − | У міжнародній системі одиниць фізичних величин (СІ) одиницею вимірювання тиску є 1 H/м<sup>2</sup> - паскаль (Па). Зручнішим для використання є кратні одиниці - гектопаскаль (гПа), кілопаскаль (кПа) і мегапаскаль (МПа): 1 гПа = 100 Па, 1 кПа = 1000 Па, 1 МПа = 10<sup>6</sup> Па. | + | ==Одиниці вимірювання == |
| + | Вимірюється в одиницях висоти стовпа рідини або в одиницях тиску. | ||
| + | |||
| + | У системі МКГСС гідростатичний тиск вимірюється в кгс/м<sup>2</sup>. | ||
| + | |||
| + | У міжнародній системі одиниць фізичних величин (СІ) одиницею вимірювання тиску є 1 H/м<sup>2</sup> - паскаль (Па). Зручнішим для використання є кратні одиниці - гектопаскаль (гПа), кілопаскаль (кПа) і мегапаскаль (МПа): 1 гПа = 100 Па, 1 кПа = 1000 Па, 1 МПа = 10<sup>6</sup> Па. | ||
| + | Високий тиск часто виражають в атмосферах, приймаючи за 1 атм. тиск в 101325 Па або 760 мм ртутного стовпчика при температурі 0 градусів по шкалі Цельсія, густині ртуті 13595,1 кг/м<sup>3</sup> і нормальному прискоренні вільного падіння 9,80665 м/с<sup>2</sup>. | ||
== Властивості гідростатичного тиску == | == Властивості гідростатичного тиску == | ||
[[Файл:1_властивість_гідростатичного_тиску.jpg|200px|thumb|right| Рис. Перша Властивість гідростатичного тиску]] | [[Файл:1_властивість_гідростатичного_тиску.jpg|200px|thumb|right| Рис. Перша Властивість гідростатичного тиску]] | ||
| − | ''' ''Властивість 1''''' | + | *''' ''Властивість 1''''' |
| − | Гідростатичний тиск завжди по внутрішній нормалі, | + | |
| + | ''Гідростатичний тиск завжди спрямований до площини, на яку він діє, по внутрішній нормалі.'' | ||
| + | |||
| + | Розглянемо силу гідростатичного тиску <math>p</math>, прикладену в точці С під кутом до поверхні А - В об'єму рідини, який знаходиться в стані рівноваги (рис.).Цю силу можна розкласти на: нормальну силу <math>P_n</math> і дотичну силу <math>P_t</math> до поверхні А - В. | ||
| + | Отже, сила гідростатичного тиску <math>p</math> в точці С діє лише в напрямку сили <math>P_n</math>, тобто нормально до поверхні А - В.Направлена вона тільки по внутрішній нормалі. При представлені направленні сили гідростатичного тиску по зовнішній нормалі виникнуть розтягуючі сили, що призведе до руху рідини. Це перечить умові, за якою рідина має знаходитись у стані спокою.Тому сила гідростатичного тиску завжди стискуюча, тобто направлена по внутрішній нормалі. | ||
| + | |||
| + | *''' ''Властивість 2 або Основна теорема гідростатики''''' | ||
| + | [[Файл:2_властивість.jpg|200px|thumb|right| Рис. Друга Властивість гідростатичного тиску]] | ||
| + | ''Гідростатичний тиск не залежить від кута нахилу площини дії і в різних напрямках одинаковий за величиною. | ||
| + | '' | ||
| + | |||
| + | <math>p_x=p_y=p_z=p_e</math>; | ||
| + | |||
| + | Щоб довести другу властивість гідростатичного тиску виділимо в рідині, яка знаходиться в стані рівноваги, частинку в формі трикутної призми з основою у вигляді прямокутного трикутника А - В - С. Будемо розглядати цей об'єм в довільній системі координат X, Y, Z. При цьому вісь yперпендикулярна площині. На призму діють такі сили: <math>P_x</math>, <math>P_z</math>, <math>P_e</math>, а також сила тяжіння G, яка дорівнює: <math> G=gdxdydz/2</math>; | ||
| + | |||
| + | <math>P_x=p_xdzdy</math>; | ||
| + | |||
| + | <math>P_z=p_zdxdy</math>; | ||
| + | |||
| + | <math>P_e=p_ededy</math>; | ||
| + | |||
| + | Силою тяжіння можна знехтувати, оскільки ця величина буде 3-го порядку малості, а сили які діють на грані призми будуть 2-го порядку. | ||
| + | Якщо частина рідини знаходиться в стані рівноваги, то сума проекції всіх сил, прикладених до неї, в будь-якому напрямку дорівнюватиме нулю: | ||
| + | |||
| + | <math>\sum\ x=0</math>; <math>p_xdzdy-p_ededy\sin\alpha</math>; | ||
| + | |||
| + | <math>\sum\ z=0</math>; <math>p_zdxdy-p_ededy\cos\alpha</math>; | ||
| + | |||
| + | Підставивши <math>dz=de\sin\alpha</math> і <math>dx=de\cos\alpha</math> в попереднє рівняння і поділивши кожне рівняння на <math>dy</math>, отримаємо: | ||
| + | |||
| + | <math>\sum\ x=0</math>; <math>p_xdz-p_edz=0</math>; | ||
| + | |||
| + | <math>\sum\ z=0</math>; <math>p_zdx-p_edx=0</math>; | ||
| + | |||
| + | Звідки: <math>p_x=p_z=p_e</math>. | ||
| + | |||
| + | Розвернувши осі координат, можна аналогічно довести <math>p_x=p_y=p_e</math>, тобто можна вважати що: <math>p_x=p_y=p_z=p_e</math> | ||
| + | |||
| + | Отже, гідростатичний тиск на нахилену грань <math>p_e</math> рівний по велечині з гідростатичним тиском на вертикальну і горизонтальну грані. Оскільки кут нахилу грані взятий довільно, то можна стверджувати, що гідростатичний тиск в будь-якій точці рідини діє однаково у всіх напрямках. | ||
| + | |||
| + | *'''''Властивість 3 або Основне рівняння гідростатики''''' | ||
| + | |||
| + | ''При дії тільки сили ваги (так званий абсолютний спокій) гідростатичний тиск у будь-якій точці рідини на глибині <math>h</math> виражається залежністю:'' | ||
| + | |||
| + | <math> p=p_0 + \rho g h</math>. | ||
| + | |||
| + | Інший вигляд основного рівняння гідростатики: | ||
| + | |||
| + | <math>p=p_0 + \rho g (z_0 - z)</math>, | ||
| + | |||
| + | де <math>z_0, z</math> - відповідно відстані від довільної площини порівняння до вільної поверхні рідини і до точки в рідині, де тиск дорівнює <math>p</math>. | ||
| + | |||
| + | В деяких випадках зручно представити основне рівняння гідростатики і у такому вигляді: | ||
| + | |||
| + | <math>{p/ \rho g} + z = {p_0/ \rho g} + z_0 </math>. | ||
| + | |||
| + | Якщо ж на поверхні рідини тиск атмосферний, тобто <math>p_0 = p_{atm}</math>, то рівняння буде записуватись так: | ||
| + | |||
| + | <math>p_{abs} = p_{atm} + \rho g h </math>. | ||
| + | |||
| + | Щоб пояснити основне рівняння гідростатики перепишемо диференціальне рівняння Ейлера у такому вигляді: | ||
| + | |||
| + | <math>dp= \rho (\frac{{\partial \ U}}{{\partial \ x}} dx + \frac{{\partial \ U}}{{\partial \ y}} dy + \frac{{\partial \ U}}{{\partial \ z}} dz)</math>, | ||
| + | або: | ||
| + | |||
| + | <math>dp= \rho dU</math> (1). | ||
| + | |||
| + | Проінтегрувавши рівняння (1), отримаємо: | ||
| + | |||
| + | <math>p= \rho U + C</math> (2), | ||
| + | |||
| + | де <math>C</math> - стала інтегрування. | ||
| + | |||
| + | Залежність (2) дозволяє визначити гідростатичний тиск рідини, яка знаходиться в стані рівноваги під дією сил, проекції яких на осі координат дорівнюють <math>X, Y, Z</math>. Але варто згадати, що вказані проекції сил, <math>X, Y, Z</math> віднесені до одиниці маси і мають розмірність прискорення. | ||
| + | |||
| + | Для знаходження сталої інтегрування <math>C</math> необхідно мати граничні умови, тобто, наприклад, знати силу тиску <math>p_0</math> і відповідне їй значення функції <math>U_0</math> для будь-якої точки рідини.Тоді: | ||
| + | |||
| + | |||
| + | <math>p_0 = \rho U_0 + C </math>, | ||
| + | |||
| + | звідки: | ||
| + | |||
| + | <math>C = p_0 - \rho U_0</math> (3). | ||
| + | |||
| + | Підставляючи значення <math>C</math> по (3) в рівняння (2), отримаємо: | ||
| + | |||
| + | <math>p= \rho U + C = \rho U + p_0 - \rho U_0; p= p_0 + \rho (U - U_0) </math>, (4) | ||
| + | |||
| + | або: | ||
| + | |||
| + | <math>p - p_0 = \rho (U - U_0)</math> (4'). | ||
| + | |||
| + | Отже, за допомогою рівняння (4) можна визначити гідростатичний тиск в будь-якій точці рідини, якщо для цієї точки будуть відомі значення функції <math>U</math>, а також граничні умови (<math>p_0 </math> і <math>U_0</math>). Якщо взяти ряд точок, в яких гідростатичний тиск однаковий, а, отже, однакове і значення потенціальної функції <math>U</math>, і провести через ці точки площину, то вона буде називатись '''площиною рівного тиску''' або '''площиною рівного потенціалу'''. | ||
| + | |||
| + | Розглянемо найбільш важливий для практики випадок рівноваги рідини, яка знаходиться під дією лише сил тяжіння. | ||
| + | |||
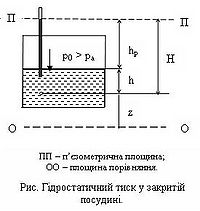
| + | Припустимо, що рідина знаходиться в закритій посудині. Також будемо вважати, що на поверхню рідини діє відомий нам тиск | ||
| + | <math>p_0</math>, відмінний від атмосферного.Тоді проекції об'ємних сил (в даному випадку сил тяжіння) на осі <math>X</math> та <math>y</math> будуть дорівнювати нулю: | ||
| + | |||
| + | <math>X = \frac{{\partial \ U}}{{\partial \ x} = 0</math> | ||
| + | і | ||
| + | <math>Y = \frac{{\partial \ U}}{{\partial \ y}} = 0</math>. | ||
| + | |||
| + | А проекція сили тяжіння на вісь <math>z</math>, буде дорівнювати: | ||
| + | |||
| + | <math>Z = \frac{{\partial \ U}}{{\partial \ z}} = - g </math>, | ||
| + | |||
| + | тому що вісь <math>z</math> має напрямок, протилежний до напрямку дії сили тяжіння. Відповідно, дифференціальне рівняння (1) для даного випадку прийме наступний вигляд: | ||
| + | |||
| + | <math>dp = - \rho g dz </math> (5), | ||
| + | |||
| + | <math>\frac{{ dp }}{{ \rho g }} + dz = 0 </math> (5'). | ||
| + | [[Файл:3_Властивість_гідростатики.jpg|300px|thumb|right|Рис. Третя властивість гідростатичного тиску]] | ||
| + | Отримане рівняння (5') є дифференціальним рівнянням рівноваги рідини, яка знаходиться під дією тільки сили тяжіння. | ||
| + | |||
| + | Проінтегрувавши рівняння (5'), отримаємо: | ||
| + | |||
| + | <math>z + \frac{{ p }}{{ \rho g }} = 0 </math> (6). | ||
| + | |||
| + | Граничні умови на поверхні рідини нам відомі: <math>z = z_0</math> і тиск <math>p = p_0 </math>. Відповідно, | ||
| + | |||
| + | <math>z_0 + \frac {{ p_0 }}{{ \rho g }} = C</math> (7). | ||
| + | |||
| + | Підставимо отримане в залежність (6) при інтеграції вільного члена <math>C</math>: | ||
| + | |||
| + | <math>z + \frac{{ p }}{{ \rho g }} = z_0 + \frac{{ p }}{{ \rho g }}</math>, | ||
| + | |||
| + | або в закінченому вигляді: | ||
| + | |||
| + | <math> p = p_0 + \rho g (z_0 - z)</math> (8). | ||
| + | |||
| + | |||
| + | Візьмемо в рідині довільну точку <math>A</math> с координатою <math>z</math> і глибиною занурення <math>h</math> (Див. рис. Третя властивість). Враховуючи, що <math>h = z_0 - z</math>, на основі залежності (8) можемо написати рівняння, яке називають '''основним рівнянням гідростатики ''' : | ||
| + | |||
| + | <math>p = p_0 + \rho g h </math>. | ||
| + | |||
| + | Виходячи з вищевикладеного можна зробити висновок, що тиск залежить від глибини занурення (висоти стовпа рідини), але не залежить від її кількості у посудині та форми посудини. А показує це рівняння, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску <math>p_0</math> і надлишкового тиску <math>\rho gh</math>. | ||
| + | |||
| + | |||
| + | ==Застосування гідростатики == | ||
| + | Закони гідростатики досліджувались і застосовувались з давніх давен і застосовуються до сьогодні. | ||
| + | Прикладами застосування гідростатики в давнину можуть слугувати розробки в країнах, які перебували в залежності від питань регулювання стоку води. І як показує історія саме ці країни одими з перших внесли великі внески в розвиток науки. До таких країн можна віднести: Італія, Голандія, в якійсь мірі Єгипет (Александрійська школа вчених), також слід віднести Грецію з її широко розвиненим суховодством. | ||
| + | |||
| + | Ще багато років до нашої ери люди задумувались над питаннями, які можна віднести до розділу "практичної гідравліки". Відомості про побудову різних водяних коліс, як для підняття води, так і для експлуатації водяної сили, системи зрошування, будівництво трубопроводів в містах Ассірії і Вавилонії, розробка інших гідротехнічних споруд (описаних в роботах Курта Меркеля "Die Ingenieurtechnik im Alterum", Berlin 1899) і т.д. переконливо свідчать про досягнення у минулому. | ||
| + | |||
| + | На сьогодні, знання з гідростатики широко використовуються на практиці. Закони гідростатики використовуються в роботі гідравлічних машин, таких як: | ||
| + | |||
| + | *Гідродвигуни; | ||
| + | |||
| + | *Гідравлічні насоси; | ||
| + | |||
| + | *Поршневі насоси; | ||
| + | |||
| + | *Центробіжні насоси; | ||
| + | |||
| + | *Роторні насоси: шестерневі насоси, гвинтові насоси, пластинчасті насоси, роторно-поршневі насоси; | ||
| + | |||
| + | *Водопідйомні пристрої: гідравлічний таран, жектори; | ||
| + | |||
| + | *Гідравлічні турбіни; | ||
| + | |||
| + | ''' Приклади застосування в інших сферах:''' завтосування гідростатичного тиску в об'ємних гідроприводах та гідрооб'ємних передачах (гідромуфта, гідротрансформатор), водопостачанні та водовідведенні, зрошувальних машинах. Широко вжитку набули гідравлічні пресси, гідравлічні домкрати, в яких визначальну і важливу роль відіграє гідростатичний тиск і його властивості. | ||
| + | |||
| + | В автомобілях використовуються гідростатичні трансмісії. Класична гідростатична трансмісія дозволяє акумулювати енергію масла під тиском у спеціальній ємності на короткий період. Це досить зручно для автомобіля зі споживанням енергії через правильні короткі інтервали, наприклад, для міського автобуса. | ||
| + | |||
| + | |||
| + | ==Джерела == | ||
| + | |||
| + | * А. А. Угинчус "Гидравлика и гидравлические машины", Харьков 1966 | ||
| + | |||
| + | * П. Е. Осипов "Гидравлика, гидравлические машины и гидропривод",издание 3, Москва, "Лесная Промышленнось", 1981 | ||
| + | |||
| + | * А. Д. Альтштуль, П. Г. Киселев "Гидравлика и аэродинамика", Москва, Стройиздат, 1975 | ||
| + | |||
| + | * Б. М. Завойко, Н. П. Лещій "Технічна механіка рідин і газів: основні теоретичні положення та задачі", Львів, "Новий світ", 2004 | ||
| − | + | * Вікіпедія [http://uk.wikipedia.org/wiki/Гідростатичний_тиск Гідростатичний тиск] | |
| − | |||
Поточна версія на 12:43, 5 травня 2012
Зміст
Поняття "гідростатичний тиск"
Гідростатичний тиск [math]p[/math] (рос.гидростатическое давление, англ. hydrostatic pressure, нім. Wasserdruckhöne) -
- це тиск рідини в будь-якій точці об'єму цієї рідини. Тиск у рідині, що перебуває у стані спокою, створений сумою тиску газу на її вільній поверхні і зумовленого силою тяжіння тиску стовпа рідини, розташованого над точкою вимірювання. Г. т. залежить від глибини занурення.
- це напруга стиску в точці, розміщеній всередині рідини, що знаходиться в стані спокою:
[math]\ p = \lim_{\Delta \omega\to\0}\frac{{\Delta \ P}}{{\Delta \omega}}[/math],
де [math]\Delta \ P[/math] - сила тиску, що діє на елементарну площинку [math]\Delta \omega[/math], яка включає в собі дану точку.
В гідрогеології поняття гідростатичного тиску трактується ширше: гідростатичний тиск - це тиск рідини (рухомої або нерухомої) у певній точці водоносної системи. Тобто гідростатичний тиск — загальна величина трьох головних напружень в будь-якій точці гірничого масиву, що перебуває в стані спокою. Високий гідростатичний тиск сприяє обваленню порід покрівлі та підйому підошви виробки, де спостерігаються раптові прориви вод і пливунів.
На зовнішній поверхні рідини гідростатичний тиск завжди спрямований по нормалі до площини, на яку він діє, а в будь-якій точці всередині рідини його величина не залежить від орієнтації площинки в просторі. Він є лише функцією координат.
Одиниці вимірювання
Вимірюється в одиницях висоти стовпа рідини або в одиницях тиску.
У системі МКГСС гідростатичний тиск вимірюється в кгс/м2.
У міжнародній системі одиниць фізичних величин (СІ) одиницею вимірювання тиску є 1 H/м2 - паскаль (Па). Зручнішим для використання є кратні одиниці - гектопаскаль (гПа), кілопаскаль (кПа) і мегапаскаль (МПа): 1 гПа = 100 Па, 1 кПа = 1000 Па, 1 МПа = 106 Па.
Високий тиск часто виражають в атмосферах, приймаючи за 1 атм. тиск в 101325 Па або 760 мм ртутного стовпчика при температурі 0 градусів по шкалі Цельсія, густині ртуті 13595,1 кг/м3 і нормальному прискоренні вільного падіння 9,80665 м/с2.
Властивості гідростатичного тиску
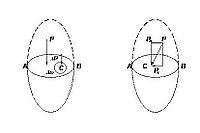
- Властивість 1
Гідростатичний тиск завжди спрямований до площини, на яку він діє, по внутрішній нормалі.
Розглянемо силу гідростатичного тиску [math]p[/math], прикладену в точці С під кутом до поверхні А - В об'єму рідини, який знаходиться в стані рівноваги (рис.).Цю силу можна розкласти на: нормальну силу [math]P_n[/math] і дотичну силу [math]P_t[/math] до поверхні А - В. Отже, сила гідростатичного тиску [math]p[/math] в точці С діє лише в напрямку сили [math]P_n[/math], тобто нормально до поверхні А - В.Направлена вона тільки по внутрішній нормалі. При представлені направленні сили гідростатичного тиску по зовнішній нормалі виникнуть розтягуючі сили, що призведе до руху рідини. Це перечить умові, за якою рідина має знаходитись у стані спокою.Тому сила гідростатичного тиску завжди стискуюча, тобто направлена по внутрішній нормалі.
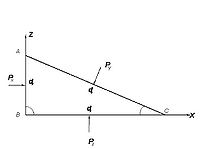
- Властивість 2 або Основна теорема гідростатики
Гідростатичний тиск не залежить від кута нахилу площини дії і в різних напрямках одинаковий за величиною.
[math]p_x=p_y=p_z=p_e[/math];
Щоб довести другу властивість гідростатичного тиску виділимо в рідині, яка знаходиться в стані рівноваги, частинку в формі трикутної призми з основою у вигляді прямокутного трикутника А - В - С. Будемо розглядати цей об'єм в довільній системі координат X, Y, Z. При цьому вісь yперпендикулярна площині. На призму діють такі сили: [math]P_x[/math], [math]P_z[/math], [math]P_e[/math], а також сила тяжіння G, яка дорівнює: [math]G=gdxdydz/2[/math];
[math]P_x=p_xdzdy[/math];
[math]P_z=p_zdxdy[/math];
[math]P_e=p_ededy[/math];
Силою тяжіння можна знехтувати, оскільки ця величина буде 3-го порядку малості, а сили які діють на грані призми будуть 2-го порядку. Якщо частина рідини знаходиться в стані рівноваги, то сума проекції всіх сил, прикладених до неї, в будь-якому напрямку дорівнюватиме нулю:
[math]\sum\ x=0[/math]; [math]p_xdzdy-p_ededy\sin\alpha[/math];
[math]\sum\ z=0[/math]; [math]p_zdxdy-p_ededy\cos\alpha[/math];
Підставивши [math]dz=de\sin\alpha[/math] і [math]dx=de\cos\alpha[/math] в попереднє рівняння і поділивши кожне рівняння на [math]dy[/math], отримаємо:
[math]\sum\ x=0[/math]; [math]p_xdz-p_edz=0[/math];
[math]\sum\ z=0[/math]; [math]p_zdx-p_edx=0[/math];
Звідки: [math]p_x=p_z=p_e[/math].
Розвернувши осі координат, можна аналогічно довести [math]p_x=p_y=p_e[/math], тобто можна вважати що: [math]p_x=p_y=p_z=p_e[/math]
Отже, гідростатичний тиск на нахилену грань [math]p_e[/math] рівний по велечині з гідростатичним тиском на вертикальну і горизонтальну грані. Оскільки кут нахилу грані взятий довільно, то можна стверджувати, що гідростатичний тиск в будь-якій точці рідини діє однаково у всіх напрямках.
- Властивість 3 або Основне рівняння гідростатики
При дії тільки сили ваги (так званий абсолютний спокій) гідростатичний тиск у будь-якій точці рідини на глибині [math]h[/math] виражається залежністю:
[math]p=p_0 + \rho g h[/math].
Інший вигляд основного рівняння гідростатики:
[math]p=p_0 + \rho g (z_0 - z)[/math],
де [math]z_0, z[/math] - відповідно відстані від довільної площини порівняння до вільної поверхні рідини і до точки в рідині, де тиск дорівнює [math]p[/math].
В деяких випадках зручно представити основне рівняння гідростатики і у такому вигляді:
[math]{p/ \rho g} + z = {p_0/ \rho g} + z_0[/math].
Якщо ж на поверхні рідини тиск атмосферний, тобто [math]p_0 = p_{atm}[/math], то рівняння буде записуватись так:
[math]p_{abs} = p_{atm} + \rho g h[/math].
Щоб пояснити основне рівняння гідростатики перепишемо диференціальне рівняння Ейлера у такому вигляді:
[math]dp= \rho (\frac{{\partial \ U}}{{\partial \ x}} dx + \frac{{\partial \ U}}{{\partial \ y}} dy + \frac{{\partial \ U}}{{\partial \ z}} dz)[/math], або:
[math]dp= \rho dU[/math] (1).
Проінтегрувавши рівняння (1), отримаємо:
[math]p= \rho U + C[/math] (2),
де [math]C[/math] - стала інтегрування.
Залежність (2) дозволяє визначити гідростатичний тиск рідини, яка знаходиться в стані рівноваги під дією сил, проекції яких на осі координат дорівнюють [math]X, Y, Z[/math]. Але варто згадати, що вказані проекції сил, [math]X, Y, Z[/math] віднесені до одиниці маси і мають розмірність прискорення.
Для знаходження сталої інтегрування [math]C[/math] необхідно мати граничні умови, тобто, наприклад, знати силу тиску [math]p_0[/math] і відповідне їй значення функції [math]U_0[/math] для будь-якої точки рідини.Тоді:
[math]p_0 = \rho U_0 + C[/math],
звідки:
[math]C = p_0 - \rho U_0[/math] (3).
Підставляючи значення [math]C[/math] по (3) в рівняння (2), отримаємо:
[math]p= \rho U + C = \rho U + p_0 - \rho U_0; p= p_0 + \rho (U - U_0)[/math], (4)
або:
[math]p - p_0 = \rho (U - U_0)[/math] (4').
Отже, за допомогою рівняння (4) можна визначити гідростатичний тиск в будь-якій точці рідини, якщо для цієї точки будуть відомі значення функції [math]U[/math], а також граничні умови ([math]p_0[/math] і [math]U_0[/math]). Якщо взяти ряд точок, в яких гідростатичний тиск однаковий, а, отже, однакове і значення потенціальної функції [math]U[/math], і провести через ці точки площину, то вона буде називатись площиною рівного тиску або площиною рівного потенціалу.
Розглянемо найбільш важливий для практики випадок рівноваги рідини, яка знаходиться під дією лише сил тяжіння.
Припустимо, що рідина знаходиться в закритій посудині. Також будемо вважати, що на поверхню рідини діє відомий нам тиск [math]p_0[/math], відмінний від атмосферного.Тоді проекції об'ємних сил (в даному випадку сил тяжіння) на осі [math]X[/math] та [math]y[/math] будуть дорівнювати нулю:
[math]X = \frac{{\partial \ U}}{{\partial \ x} = 0[/math] і [math]Y = \frac{{\partial \ U}}{{\partial \ y}} = 0[/math].
А проекція сили тяжіння на вісь [math]z[/math], буде дорівнювати:
[math]Z = \frac{{\partial \ U}}{{\partial \ z}} = - g[/math],
тому що вісь [math]z[/math] має напрямок, протилежний до напрямку дії сили тяжіння. Відповідно, дифференціальне рівняння (1) для даного випадку прийме наступний вигляд:
[math]dp = - \rho g dz[/math] (5),
[math]\frac{{ dp }}{{ \rho g }} + dz = 0[/math] (5').
Отримане рівняння (5') є дифференціальним рівнянням рівноваги рідини, яка знаходиться під дією тільки сили тяжіння.
Проінтегрувавши рівняння (5'), отримаємо:
[math]z + \frac{{ p }}{{ \rho g }} = 0[/math] (6).
Граничні умови на поверхні рідини нам відомі: [math]z = z_0[/math] і тиск [math]p = p_0[/math]. Відповідно,
[math]z_0 + \frac {{ p_0 }}{{ \rho g }} = C[/math] (7).
Підставимо отримане в залежність (6) при інтеграції вільного члена [math]C[/math]:
[math]z + \frac{{ p }}{{ \rho g }} = z_0 + \frac{{ p }}{{ \rho g }}[/math],
або в закінченому вигляді:
[math]p = p_0 + \rho g (z_0 - z)[/math] (8).
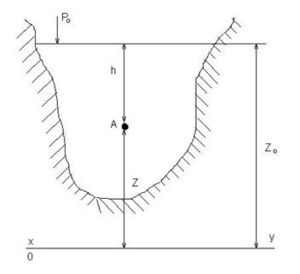
Візьмемо в рідині довільну точку [math]A[/math] с координатою [math]z[/math] і глибиною занурення [math]h[/math] (Див. рис. Третя властивість). Враховуючи, що [math]h = z_0 - z[/math], на основі залежності (8) можемо написати рівняння, яке називають основним рівнянням гідростатики :
[math]p = p_0 + \rho g h[/math].
Виходячи з вищевикладеного можна зробити висновок, що тиск залежить від глибини занурення (висоти стовпа рідини), але не залежить від її кількості у посудині та форми посудини. А показує це рівняння, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску [math]p_0[/math] і надлишкового тиску [math]\rho gh[/math].
Застосування гідростатики
Закони гідростатики досліджувались і застосовувались з давніх давен і застосовуються до сьогодні. Прикладами застосування гідростатики в давнину можуть слугувати розробки в країнах, які перебували в залежності від питань регулювання стоку води. І як показує історія саме ці країни одими з перших внесли великі внески в розвиток науки. До таких країн можна віднести: Італія, Голандія, в якійсь мірі Єгипет (Александрійська школа вчених), також слід віднести Грецію з її широко розвиненим суховодством.
Ще багато років до нашої ери люди задумувались над питаннями, які можна віднести до розділу "практичної гідравліки". Відомості про побудову різних водяних коліс, як для підняття води, так і для експлуатації водяної сили, системи зрошування, будівництво трубопроводів в містах Ассірії і Вавилонії, розробка інших гідротехнічних споруд (описаних в роботах Курта Меркеля "Die Ingenieurtechnik im Alterum", Berlin 1899) і т.д. переконливо свідчать про досягнення у минулому.
На сьогодні, знання з гідростатики широко використовуються на практиці. Закони гідростатики використовуються в роботі гідравлічних машин, таких як:
- Гідродвигуни;
- Гідравлічні насоси;
- Поршневі насоси;
- Центробіжні насоси;
- Роторні насоси: шестерневі насоси, гвинтові насоси, пластинчасті насоси, роторно-поршневі насоси;
- Водопідйомні пристрої: гідравлічний таран, жектори;
- Гідравлічні турбіни;
Приклади застосування в інших сферах: завтосування гідростатичного тиску в об'ємних гідроприводах та гідрооб'ємних передачах (гідромуфта, гідротрансформатор), водопостачанні та водовідведенні, зрошувальних машинах. Широко вжитку набули гідравлічні пресси, гідравлічні домкрати, в яких визначальну і важливу роль відіграє гідростатичний тиск і його властивості.
В автомобілях використовуються гідростатичні трансмісії. Класична гідростатична трансмісія дозволяє акумулювати енергію масла під тиском у спеціальній ємності на короткий період. Це досить зручно для автомобіля зі споживанням енергії через правильні короткі інтервали, наприклад, для міського автобуса.
Джерела
- А. А. Угинчус "Гидравлика и гидравлические машины", Харьков 1966
- П. Е. Осипов "Гидравлика, гидравлические машины и гидропривод",издание 3, Москва, "Лесная Промышленнось", 1981
- А. Д. Альтштуль, П. Г. Киселев "Гидравлика и аэродинамика", Москва, Стройиздат, 1975
- Б. М. Завойко, Н. П. Лещій "Технічна механіка рідин і газів: основні теоретичні положення та задачі", Львів, "Новий світ", 2004
- Вікіпедія Гідростатичний тиск